Heapsort

Der Heapsort (Sortieren mit einer Halde) ist eine Variante des Sortierens durch Auswahl. Er wurde in den 1960er Jahren von Robert W. Floyd und J. W. J. Williams entwickelt (siehe: Artikel in Wikipedia).

Der Heapsort hat den Vorteil, dass er auch im ungünstigsten Fall in der Lage ist mit einem Aufwand von O(N*log(N)) zu sortieren.

Hierfür wird eine Datenstruktur (der Heap) verwendet mit der die Bestimmung des Maximums einer Folge in einem Schritt möglich ist.

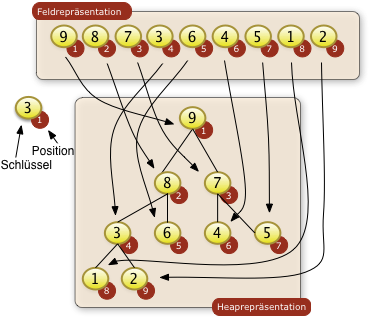Heap und Feldrepräsentation

Beim Heapsort werden die zu sortierenden Schlüssel einer Folge in zwei Repräsentation betrachet:

  • Feldrepräsentation: Die Folge der unsortierten Schlüssel in einem Feld die sortiert werden soll. Am Ende des Heapsorts soll diese Folge als Feld aufsteigend sortiert sein.
  • Heaprepräsentation: Eine interne Repräsentation auf der die Regeln des Heapsorts angewendet werden. Diese Heaprepräsentation in der Form eines Binärbaums dient ausschließlich dem Verständnis des Betrachters

Beide Repräsentationen sind Sichten auf die gleichen Daten. Beim Heapsort werden nicht die Schlüssel in einen Binärbaum umkopiert. Die Heaprepräsentation dient nur dem Betrachter zur Verdeutlichung der Beziehung gewisser Feldpositionen.

Die Grundidee des Heapsorts besteht darin, daß an der Wurzel des Binärbaums immer der größte Schlüssel stehen muss. Diesen größten Schlüssel kann man dann dem Binärbaum entnehmen und als größtes Element der Folge benutzen. Die verbliebene unsortierte Teilfolge muss dann wieder so als ein Baum organisiert werden in dem das größte Element an der Wurzel steht. Durch sukzessives Entnehmen der verbliebenen gößten Elemente kann man die gesamte Folge sortieren.

Beim Heapsort muss nicht nur an der Wurzel des Baums der größte Schlüssel stehen. Jeder Knoten im Binärbaum muss größer als die Unterknoten sein. Diese Bedingung nennt man die Heapbedingung.

Verfahren

Beim Heapsort wird auf eine Feld mit N unsortierten Schlüsseln das folgende Verfahren wiederholt angewendet:

  • Herstellen der Heapbedingung  durch das Bootom-Up für ein Feld mit N Schlüsseln
  • Tauschen des ersten und größten Schlüssels auf der Position 1 mit dem letzten unsortierten Schlüssel auf Position N.
    • Wiederherstellen des Heapbedingung durch Versickern (Top-Down Verfahren)
  • Wiederholen des Verfahrens für die Positionen 1 bis N-1. Ab der Position N ist das Feld schon sortiert.

Beispiel

Grafische Visualisierung Beschreibung
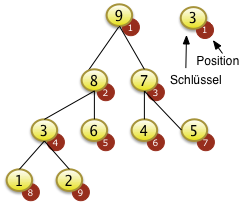Beispiel Heapkriterium

Das Beispiel links zeigt nicht eine vollständige Sortierung der gesamten Folge.

Es zeigt nur das Einsortieren eines Elements für eine Feldstruktur die schon der Heapbedingung genügt.

Das Feld mit den N=9 Elementen wurde so vorsortiert, dass es der Heapdebingung genügt. Das Herstellen der Heapbedingung wird später erläutert.
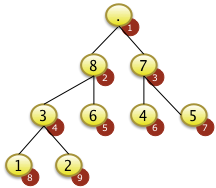Beispiel Heapkriterium

Das Element mit dem Schlüssel 9 wird von der Spitze des Baums f[1] entfernt...
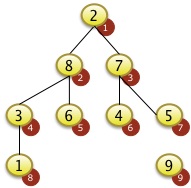Beispiel Heapkriterium

... und mit dem Wert 2 der Position N=9 getauscht. Der größte Schlüssel der Folge befindet sich jetzt auf der Position 9.

Alle Elemente ab f[9]= F[N] aufwärts sind jetzt aufsteigend sortiert.

Alle Elemente von f[1] bis f[N-1]=f[8] sind unsortiert und müssen noch sortiert werden.

Die Elemente von f[1] bis f[8] genügen auch nicht mehr der Heapbedingung. Der Wert f[1]=2 ist nicht größer als f[2]=8 oder f[3]=7

Weitere Ressourcen

Implementierung

Die Implementierung der Klasse HeapSort.java ist bei Github zu finden.