Mit dem Bottom-Up Verfahren kann man die Heapbedingung für vollständig unsortierte Folgen von Schlüsseln herstellen.
Das Verfahren basiert auf der Idee, dass beginnend mit dem Schlüssel auf der höchsten Feldposition f[N] der Wert versickert wird um anschließend den nächst niedrigeren Wert F[N-1] zu versickern bis man den größten Wert f[1] versickert hat.
Beispiel
| Grafische Visualisierung | Beschreibung |
|---|---|
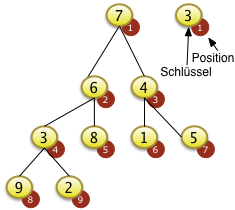 |
Der gegebene Baum sei vollständig mit Zufallsschlüsseln belegt. Alle Werte sind zufällig. Die Positionen 5, 6,7,8 und 9 können nicht versickert werden, da sie keine Unterblattknoten zum Versickern haben. |
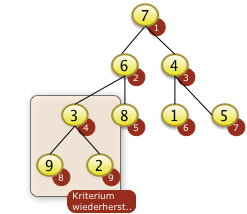 |
Das Bottom-Up Verfahren beginnt mit dem ersten Knoten i der über Unterknoten verfügt. Dieser Knoten ist immer die Position N/2 abgerundet. Bei N=9 ist die 9/2= 4.5. Der abgerundete Wert ist i=4. Hier muß f[8]=9 mit f[4]=3 getauscht werden um den Schlüssel zu versickern. |
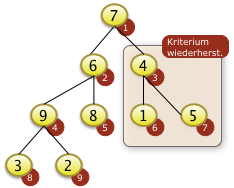 |
Bei i=3 muss f[3]=4 mit f[7]=5 getauscht werden und ist damit auch versickert. |
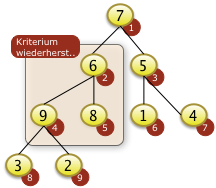 |
Bei i=2 muss f[4] mit f[2] getauscht werden. Das rekursives Versickern bei f[4]=9 is nicht notwendig. f[4]=9 ist größer als f[8]=3 und f[9]=2 |
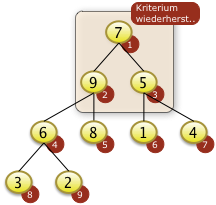 |
Bei i=1 muss f[1] mit f[2]=9 getauscht werden.
|
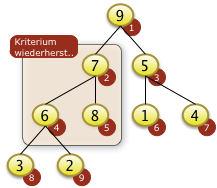 |
Nach dem Neubesetzen der Position f[2]=7 zeigt sich aber, dass die Heapbedingung für den entsprechenden Teilbaum von f[2] nicht gilt da f[2|<f[2*i+1] ist. f[2] muss also rekursiv weiter versickert werden. |
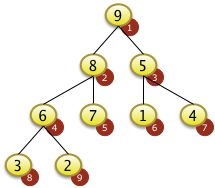 |
Nach dem Tauschen von f[2]=7 mit f[5]=8 ist das rekursive Versickern beendet. f[5] hat keine Unterknoten da 5 > N/2 ist. Der Baum genügt jetzt der Heapbedingung |
- Printer-friendly version
- Log in to post comments
- 10585 views
3ter Schritt...
Beim dritten Schritt müsste es doch f[4]=6 sein,welches größer ist als f[8] und f[9]...?
Bei i=2 muss f[4] mit f[2] getauscht werden. Das rekursives Versickern bei f[4]=9(6) ist nicht notwendig. f[4]=9(nicht 6?) ist größer als f[8]=3 und f[9]=2
typo
[...]
Schritt 2:
Der gegebene Baum sei vollständig mit Zufallsschlüsseln belegt. Alle Werte sind zufällig.
[...]
Danke
Wurde verbessert.
Positionen
1. Spalte:
Die Schlüssel f[9] bis f[5] können nicht versickert werden, da sie keine Blattknoten zum Versickern haben.
Danke, wurde verbessert.
Danke, wurde verbessert.