Hashverfahren helfen Datensätze zu speichern und effizient Operationen wie Suchen, Einfügen und Entfernen zu unterstützen.
Die Datensätze werden mit Hilfe eines eindeutigen Schlüssels gesucht bzw. sortiert. Die Idee der Hashverfahren basiert auf dem Fakt, dass in einer zu verwaltenden Menge, die Anzahl der Schlüssel normalerweise deutlich kleiner als die Wertemenge K der Schlüssel ist. Zu jedem Zeitpunkt ist also nur eine (kleine) Teilmenge K aller möglichlichen Schlüssel gespeichert. Dies geschehe in einem linearen Feld mit Indizes 0, ... , m-1. Diese nennt man Hashtabelle. m ist die Größe der Hashtabelle.
Eine Hashfunktion h ordnet jedem Schlüssel k einen Index h(k) zu. Für h(k) gilt: 0 <= h(k) <) m-1. Im Allgemeinen ist m-1 sehr viel kleiner als der Wertebereich der Schlüssel. Die Hashfunktion kann im Allgemeinen nicht injektiv und weist unterschiedlichen Werten die gleiche Hashadresse zu.
Zwei Schlüssel h(k) und h(k') mit h(k)=h(k') nennt man Synonyme.
Treten in der Menge K keine Synonyme auf, können Sie direkt in der Hashtabelle an der entsprechenden Stelle gespeichert werden.
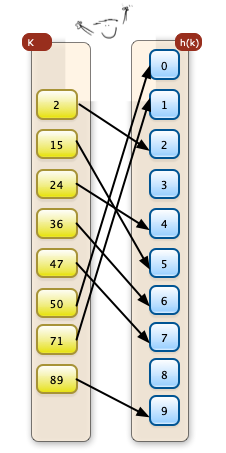
Im folgenden Beispiel wird als h(k) h(k)= k mod 10 verwendet. Es wird hier also von jeder Jahl der Rest einer Division durch 10 verwendet (Man könnte auch sagen die letzte Stelle...)
|
Hier treten keine Synonyme auf. Die Abildung ist eineindeutig.
|
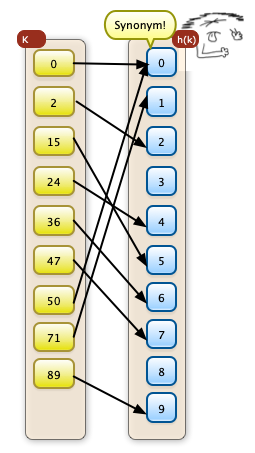
Hier tritt eine Kollision mit Synonymen auf die Werte 0 und 50 werden auf den Tabellenwert 0 abgebildet.
|
Treten Synonyme auf, ist dies schlecht für ein Hashverfahren. Der konstante Aufwand der Berechnung der Hashfunktion und der Zugriff im Feld führen zu einer Kollision die aufgelöst werden muss.
Ein Hashverfahren soll
- möglichst wenige Kollisionen aufweisen
- Adresskollisionen sollen möglichst effizient aufgelöst werden
| Aufwand | minimaler Aufw. | maximaler Aufw. | Kommentar |
|---|---|---|---|
| Suchen/Einfügen | O(1) | O(n) | Das Auftreten von Synonymen macht den Unterschied! |
Die Berechnung der Hashfunktion sollte einen konstanten Aufwand haben.
Der Zugriffsaufwand steigt aber beim Auftreten von Kollisionen. Die Probleme bei den Hashverfahren liegen in der Auflösung von Kollisionen und beim Wachsen über die Größe eines Feldes. Für eine tiefere Diskussion fehlt in dieser Vorlesung leider die Zeit. Anbei zwei gängige Strategien:
Hashverfahren mit Verkettung der Überläufer
|
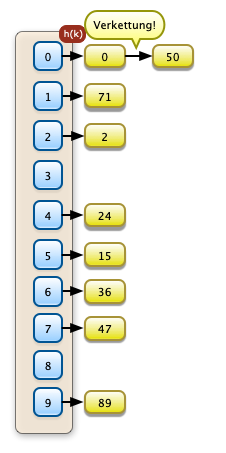
Ein Lösungsansatz besteht in der Verkettung von Überläufern deren Hashfunktion Synonyme produziert. Dies geschieht rechts bei den Werten 0 und 50. Der Zugriffsaufwand ohne Synonyme für EInfügen und Lesen ist hier O(1). Liegen Synonyme vor ist der Aufwand O(n). Die Verkettung funktioniert wenn in die Hashtabelle nur Zeiger eingetragen werden. |
 |
Offene Hashverfahren
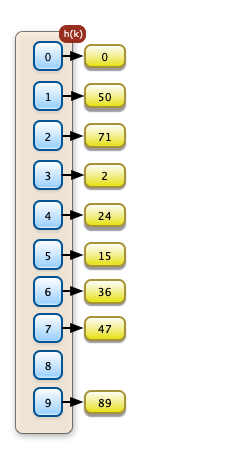 |
Sollen die Objekte direkt im Feld gespeichert werden, muß man sich im Feld einen neuen Platz suchen. Im Schaubild links, wurde zuerst die "0" auf ihrem Platz korrekt eingetragen. Als nächstes wurde die "50" eingetragen. Für sie war der Platz 0 schon belegt. Sie wurde auf dem Platz 1 eingetragen. Dann wurde die "71" eingetragen. Ihre Position 1 war schon belegt. Sie wurde auf der Position 2 eingetragen. Der Eintrag der "2" auf der Position 2 war auch nicht mehr möglich. Sie musste auf der Position 3 gespeichert werden. Ein Überläufer kann hier einen Ketteneffekt produzieren. Das Einfügen und das Finden können aufwendiger werden. Diese Operationen können im schlimmsten Fall den Aufwand O(n) haben. |
Hashverfahren robust gegen Sonderfälle zu machen ist recht aufwendig und sprengt den Rahmen dieser Vorlesung.
- Printer-friendly version
- Log in to post comments
- 521 views