Heapsort
HeapsortDer Heapsort (Sortieren mit einer Halde) ist eine Variante des Sortierens durch Auswahl. Er wurde in den 1960er Jahren von Robert W. Floyd und J. W. J. Williams entwickelt (siehe: Artikel in Wikipedia).
Der Heapsort hat den Vorteil, dass er auch im ungünstigsten Fall in der Lage ist mit einem Aufwand von O(N*log(N)) zu sortieren.
Hierfür wird eine Datenstruktur (der Heap) verwendet mit der die Bestimmung des Maximums einer Folge in einem Schritt möglich ist.
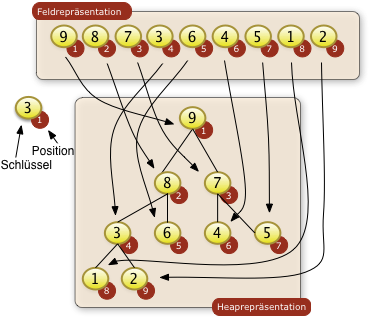 |
Beim Heapsort werden die zu sortierenden Schlüssel einer Folge in zwei Repräsentation betrachet:
Beide Repräsentationen sind Sichten auf die gleichen Daten. Beim Heapsort werden nicht die Schlüssel in einen Binärbaum umkopiert. Die Heaprepräsentation dient nur dem Betrachter zur Verdeutlichung der Beziehung gewisser Feldpositionen. Die Grundidee des Heapsorts besteht darin, daß an der Wurzel des Binärbaums immer der größte Schlüssel stehen muss. Diesen größten Schlüssel kann man dann dem Binärbaum entnehmen und als größtes Element der Folge benutzen. Die verbliebene unsortierte Teilfolge muss dann wieder so als ein Baum organisiert werden in dem das größte Element an der Wurzel steht. Durch sukzessives Entnehmen der verbliebenen gößten Elemente kann man die gesamte Folge sortieren. |
Beim Heapsort muss nicht nur an der Wurzel des Baums der größte Schlüssel stehen. Jeder Knoten im Binärbaum muss größer als die Unterknoten sein. Diese Bedingung nennt man die Heapbedingung.
Verfahren
Beim Heapsort wird auf eine Feld mit N unsortierten Schlüsseln das folgende Verfahren wiederholt angewendet:
- Herstellen der Heapbedingung durch das Bootom-Up für ein Feld mit N Schlüsseln
- Tauschen des ersten und größten Schlüssels auf der Position 1 mit dem letzten unsortierten Schlüssel auf Position N.
- Wiederherstellen des Heapbedingung durch Versickern (Top-Down Verfahren)
- Wiederholen des Verfahrens für die Positionen 1 bis N-1. Ab der Position N ist das Feld schon sortiert.
Beispiel
| Grafische Visualisierung | Beschreibung |
|---|---|
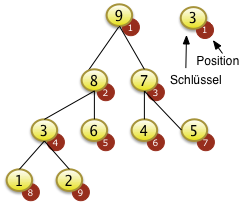 |
Das Beispiel links zeigt nicht eine vollständige Sortierung der gesamten Folge. Es zeigt nur das Einsortieren eines Elements für eine Feldstruktur die schon der Heapbedingung genügt. Das Feld mit den N=9 Elementen wurde so vorsortiert, dass es der Heapdebingung genügt. Das Herstellen der Heapbedingung wird später erläutert. |
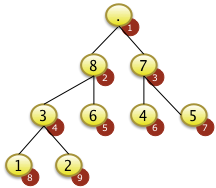 |
Das Element mit dem Schlüssel 9 wird von der Spitze des Baums f[1] entfernt... |
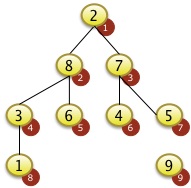 |
... und mit dem Wert 2 der Position N=9 getauscht. Der größte Schlüssel der Folge befindet sich jetzt auf der Position 9. Alle Elemente ab f[9]= F[N] aufwärts sind jetzt aufsteigend sortiert. Alle Elemente von f[1] bis f[N-1]=f[8] sind unsortiert und müssen noch sortiert werden. Die Elemente von f[1] bis f[8] genügen auch nicht mehr der Heapbedingung. Der Wert f[1]=2 ist nicht größer als f[2]=8 oder f[3]=7 |
Weitere Ressourcen
- Sehr schöne Visualisierung der Universität San Francisco (gefunden von der WIMBIT20A!)
Implementierung
Die Implementierung der Klasse HeapSort.java ist bei Github zu finden.
- 5815 views
Die Heapbedingung
Die HeapbedingungEin Feld f[1] bis f[N] mit Schlüsseln bildet einen Heap wenn die folgende Bedingung gilt:
| Heapbedingung |
|---|
|
f[i]<=f[i/2] für 2<= i <= N] |
Die Heapbedingung lässt sich leichter grafisch in einer Baumdarstellung verdeutlichen:
 |
Das Feld f mit der Feldgröße N=9
genügt der Heapbedingung da jeder obere Knoten größer als die beiden Unterknoten ist. Die Position im Feld wird hier in rot dargestellt. Der Schlüssel (Wert) des Feldelements hat einen gelben Hintergrund |
- 5196 views
Herstellen der Heapbedingung für einen unsortierten Heap (Bottom-Up Methode)
Herstellen der Heapbedingung für einen unsortierten Heap (Bottom-Up Methode)Mit dem Bottom-Up Verfahren kann man die Heapbedingung für vollständig unsortierte Folgen von Schlüsseln herstellen.
Das Verfahren basiert auf der Idee, dass beginnend mit dem Schlüssel auf der höchsten Feldposition f[N] der Wert versickert wird um anschließend den nächst niedrigeren Wert F[N-1] zu versickern bis man den größten Wert f[1] versickert hat.
Beispiel
| Grafische Visualisierung | Beschreibung |
|---|---|
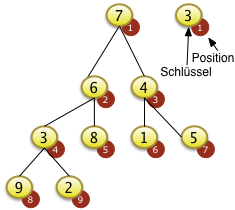 |
Der gegebene Baum sei vollständig mit Zufallsschlüsseln belegt. Alle Werte sind zufällig. Die Positionen 5, 6,7,8 und 9 können nicht versickert werden, da sie keine Unterblattknoten zum Versickern haben. |
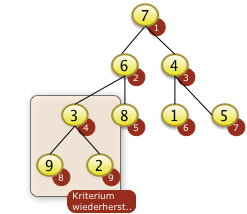 |
Das Bottom-Up Verfahren beginnt mit dem ersten Knoten i der über Unterknoten verfügt. Dieser Knoten ist immer die Position N/2 abgerundet. Bei N=9 ist die 9/2= 4.5. Der abgerundete Wert ist i=4. Hier muß f[8]=9 mit f[4]=3 getauscht werden um den Schlüssel zu versickern. |
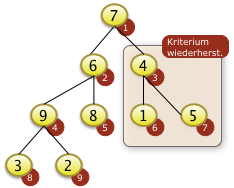 |
Bei i=3 muss f[3]=4 mit f[7]=5 getauscht werden und ist damit auch versickert. |
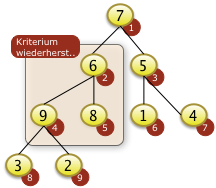 |
Bei i=2 muss f[4] mit f[2] getauscht werden. Das rekursives Versickern bei f[4]=9 is nicht notwendig. f[4]=9 ist größer als f[8]=3 und f[9]=2 |
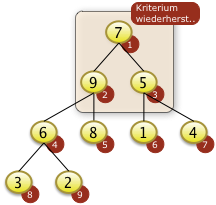 |
Bei i=1 muss f[1] mit f[2]=9 getauscht werden.
|
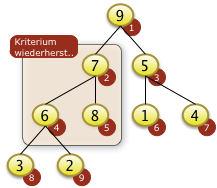 |
Nach dem Neubesetzen der Position f[2]=7 zeigt sich aber, dass die Heapbedingung für den entsprechenden Teilbaum von f[2] nicht gilt da f[2|<f[2*i+1] ist. f[2] muss also rekursiv weiter versickert werden. |
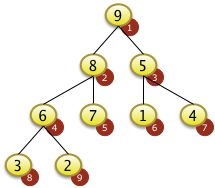 |
Nach dem Tauschen von f[2]=7 mit f[5]=8 ist das rekursive Versickern beendet. f[5] hat keine Unterknoten da 5 > N/2 ist. Der Baum genügt jetzt der Heapbedingung |
- 10585 views
3ter Schritt...
Beim dritten Schritt müsste es doch f[4]=6 sein,welches größer ist als f[8] und f[9]...?
Bei i=2 muss f[4] mit f[2] getauscht werden. Das rekursives Versickern bei f[4]=9(6) ist nicht notwendig. f[4]=9(nicht 6?) ist größer als f[8]=3 und f[9]=2
- Log in to post comments
Positionen
1. Spalte:
Die Schlüssel f[9] bis f[5] können nicht versickert werden, da sie keine Blattknoten zum Versickern haben.
- Log in to post comments
Herstellen der Heapbedingung durch Versickern (Top-Down Methode)
Herstellen der Heapbedingung durch Versickern (Top-Down Methode)Herstellen der Heapbedingung
Top-Down-Verfahren
Dieses Verfahren dient der Herstellen der Heapbedingung, wenn schon für die Unterheaps für die Heapbedingung gilt.
Man wendet es an, nachdem man den größten Schlüssel entnommen hat und ihn durch den Wert mit dem größten Index im unsortierten Baum ersetzt hat.
Das Versickern dieses neuen Schlüssels an der Wurzel des Baums erfolgt mit den folgenden Schritten:
- Beginne mit der Position i=1 im Baum
- Der Schlüssel f[i] hat keine Unterknoten da 2*i>N ist,
- Der Schlüssel kann nicht mehr versickert werden. Das Verfahren ist beendet.
- Der Schlüssel f[i] hat noch genau einen Unterknoten f[i*2]
- Der Schlüssel f[i] wird mit dem Schlüssel f[i*2] getauscht falls f[i]<f[i*2]. Das Verfahren ist nach diesem Schritt beendet.
- Der Schlüssel f[i] hat noch Unterknoten f[2*i] und f[2*i+1]
- Der Schlüssel f[i] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Das Verfahren ist beendet die Heapbedingung ist gegeben
- Der Schlüssel f[i*2] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Tausche die Schlüssel f[i] mit f[2*i]
- Versickere den Schlüssel f[i*2] nach dem Top-Down Verfahren
- Der Schlüssel f[i*2+1] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Tausche die Schlüssel f[i] mit f[2*i+1]
- Versickere den Schlüssel f[i*2+1] nach dem Top-Down Verfahren
- Der Schlüssel f[i] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
Diese rekursive Verfahren wird hier an einem Beispiel gezeigt:
| Grafische Visualisierung | Beschreibung |
|---|---|
 |
Durch das Entfernen des größten Schlüssels f[1] entstehen zwei Unterbäume für die die Heapbedingung nach wie vor gilt. |
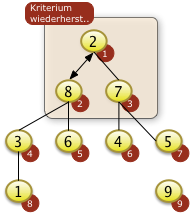 |
Durch das Einsetzen eines Schlüssel von der Position N ist nicht mehr garantiert, dass die Heapbedingung für den gesamten Restbaum f[1] bis f[N-1]=f[8] gegeben ist. Der Schlüssel f[1]=2 ist eventuell größer als die Schlüssel f[2*1] und f[2*1+1]. In diesem Fall ist die Heapbedingung für f[1] bis f[8] schon gegeben. Es muss nichts mehr getan werden. Im vorliegenden Fall ist f[1]=2 aber nicht der größte Schlüssel. Er muss rekursiv versickert werden. Dies geschieht durch das Vertauschen mit f[2] = 8. f[3] = 7 ist nicht der richtige Kandidat. 7 ist nicht der größte der drei Schlüssel. |
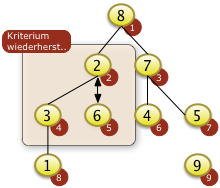 |
Nach dem Vertauschen von f[1] mit f[2] gilt die Heapbedingung zwar für den obersten Knoten. Sie gilt jedoch nicht für den Teilbaum unter f[2]= 2. Der Schlüssel 2 muss weiter versickert werden. In diesem Fall ist f[5]=6 der größte Schlüssel mit dem f[2]= 2 vertauscht weden muss. |
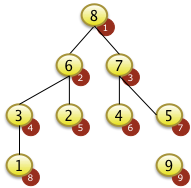 |
Nach dem Vertauschen von f[2] mit f[5] gilt die Heapbedingung wieder für den gesamten Baum. |
- 6963 views
Der Satz "Man wendet es an,
Der Satz "Man wendet es an, nachdem man den größten Schlüssel entnommen hat und ihn durch einen zufälligen Wert ersetzt hat." ist missverständlich formuliert.
Der Wert wird nicht zufällig ausgewählt, sondern ist der letzte im Baum verbliebene Knoten.
- Log in to post comments
Im Schritt 2 ist auch wieder
Im Schritt 2 ist auch wieder das "zufällig" irreführend, da der Wert ja nicht aus der Luft gezaubert wird, sondern von/auf Position N vorgegeben ist. (Ob die Werte des Heaps zufällig erstellt wurden, ist hier ja nicht von Bedeutung.)
( + typo )
"Durch das Einsetzen eines zufälligen Schlüssels von der Position N ist nicht mehr garantiert, dass die Heapbedingung für den gesamten Restbaum f[1] bis f[N-1]=f[8] gegeben ist."
- Log in to post comments
Dieses Verfahren dient der Herstellen der Heapbedingung wenn sch
Sollte geändert werden in: "Dieses Verfahren dient dem Herstellen der Heapbedingung, wenn schon für Unterheaps die Heapbedingung gilt."
- Log in to post comments
Danke, für das Feedback
Das Kommando habe ich eingefügt. Der Artikel "die" habe ich gelassen.
- Log in to post comments
Heapsort: Implementierung in Java
Heapsort: Implementierung in Javapackage s2.sort;
/**
*
* @author sschneid
* @version 2.0
*/
public class HeapSort extends Sortierer{
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public HeapSort(int[] s) {super(s,false);}
/**
* sortiert ein Eingabefeld s
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
public void sortieren(int startIndex, int endeIndex){
// Erzeugen der Heapbedingung, Bottom up...
for (int i=(endeIndex-1)/2; i>=0; i--) versickere (i,endeIndex);
//System.out.println("Heapbedingung hergestellt");
for (int i=endeIndex; i>0; i--) {
// Tausche das jeweils letzte Element mit dem Groeßten an der
// Wurzel. Versickere die neue Wurzel und verkürze
// das zu sortierende Intervall von hinten nach vorne
tausche(0,i); // Groesstes Element von der Wurzel an das Ende
// des Intervals getauscht
versickere(0,i-1); // versickere die neue Wurzel um Heapbedingung
// herzustellen
}
}
/**
* Berechne Index des linken Sohns für gegebenen Index
* liefere -1 zurück falls keine linker Sohn existiert
* @param index für den Sohn berechnet wird
* @param endeIndex letzter belegter Indexplatz
* @return
*/
private int linkerSohn(int index, int endeIndex) {
int ls = index*2+1;
if (ls > endeIndex)
return -1;
else return ls;
}
/**
* Berechne Index des linken Sohns für gegebenen Index
* liefere -1 zurück falls keine linker Sohn existiert
* @param index für den Sohn berechnet wird
* @param endeIndex letzter belegter Indexplatz
* @return
*/
private int rechterSohn(int index, int endeIndex) {
int rs = (index+1)*2;
if (rs > endeIndex)
return -1;
else return rs;
}
/**
* Versickere ein Element auf der Position "vers"
* @param vers Index des zu versickernden Elements
* @param endeIndex hoechste Indexposition die zum Verisckern zur Verfügung
* steht. Sie wird bei der Berechnung des rechts Sohns
* benötigt
*/
private void versickere (int vers, int endeIndex) {
int ls = linkerSohn(vers,endeIndex);
int rs = rechterSohn(vers,endeIndex);
int groessererSohn;
while (ls != -1) { // Es gibt einen linken Sohn
// Versickere bis Heapbedingung erfüllt ist oder keine
// Söhne mehr vorhanden sind
groessererSohn =ls; // linker Sohn als groesseren Sohn nominieren
if ((rs != -1) && (istKleiner(ls,rs))) groessererSohn = rs;
// der rechte Sohn existiert und war groesser...
if (istKleiner(vers,groessererSohn)) {
tausche(vers,groessererSohn); // beide Felder wurden getauscht
vers = groessererSohn;
ls = linkerSohn(vers,endeIndex);
rs = rechterSohn(vers,endeIndex);
}
else ls=-1; // Abbruchbedingung für while Schleife
}
}
/**
* Liefert den Namen des Heap Sorts
* @return
*/
public String algorithmus() {return "Heap Sort";}
}
- 5973 views