Verfahren
Das Sortieren durch Einfügen ist ein intuitives und elementare Verfahren:
- Man teilt die zu sortierende Folge f mit N Elementen in eine bereits sortierte Teilfolge f[0] bis f[s-1] und in eine unsortierte Teilfolge f[s] bis f[n].
- Zu Beginn ist die sortierte Teilfolge leer.
- Der Beginn der unsortierten Folge f[s] wird die Sortiergrenze genannt.
- Man setzt eine Sortiergrenze hinter der bereits durch Zufall sortierte Teilfolge f[1] bis f[s-1]
- Vergleiche f[s] mit f[s-1] und vertausche die beiden Elemente falls f[s]<f[s-1]
- Führe weitere Vergleiche und absteigende Vertauschungen durch bis man ein f[s-j] gefunden hat für das gilt f[s-j-1]<f[s-j]
- Erhöhe die Sortiergrenze von f[i] auf f[i+1] und wiederhole die Vergleichs- und Vertauschungsschritte wie im vorhergehenden Schritt beschrieben.
- Die Folge ist sortiert wenn die Sortiergrenze das Ende des Folge erreicht hat.
Beispiel
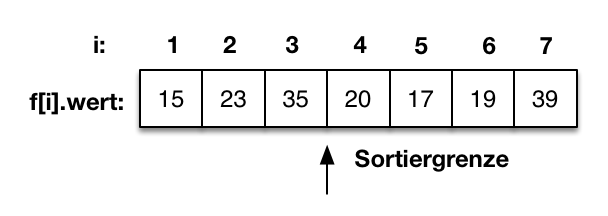 |
Gegeben sei eine Folge in einem Feld mit sieben Elementen. Die ersten drei Elemente sind bereits sortiert und die Sortiergrenze wird mit 4 belegt. Die unsortierte Folge beginnt auf dem Feldindex vier. |
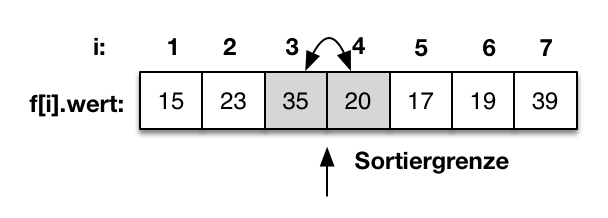 |
Als erstes wird der Wert f[4]=20 mit f[3]=35 verglichen. Da f[4] größer als f[3] ist, werden die beiden Werte getauscht. |
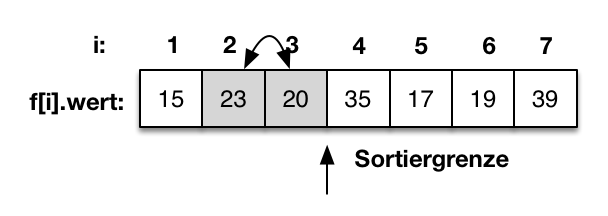 |
Anschließend folgt der Vergleich von f[3]=20 mit f[2]=23. Der Wert von f[3] ist größer als f[2]. Die beiden Werte werden getauscht. |
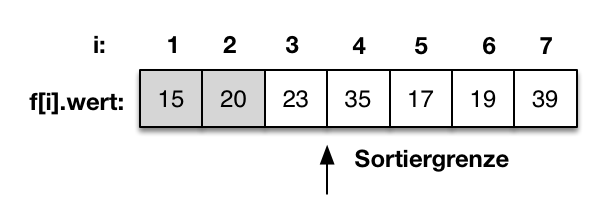 |
Der Vergleich von f[2] mit f[1] zeigt, dass f[2] größer als f[1] ist. f[2]=20 hat also seine korrekte Position in der sortierten Teilfolge gefunden. |
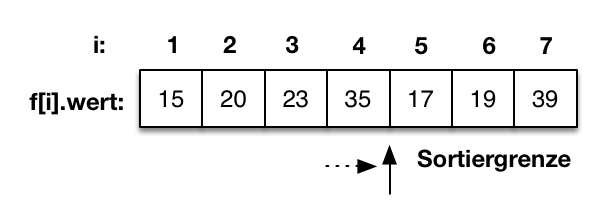 |
Der aktuelle Durchlauf ist hiermit beendet. Die Sortiergrenze wird um eins erhöht und erhält den Wert 5. |
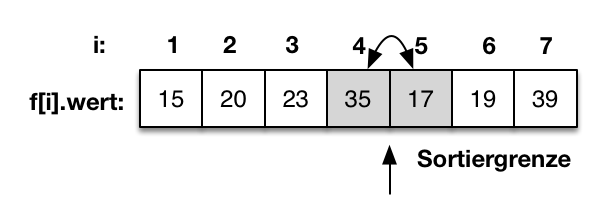 |
Die sortierte Teilfolge ist um eins größer geworden. Es wird wieder f[5]=17 mit f[4]=35 verglichen. Da f[5] größer als f[4] ist, werden die beiden Werte getauscht. Jeder Durchlauf endet, wenn der Wert nicht mehr getauscht werden muss. Der Algorithmus endet wenn die Sortiergrenze die gesamt Folge umfasst. |
Aufwand
Das Sortieren durch Einfügen braucht im günstigsten Fall nur N-1 Vergleiche für eine bereits sortierte Folge. Im ungünstigsten Fall (fallend sortiert) ist aber ein quadratisches Aufwand nötig.
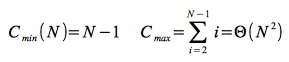
Das gleiche gilt für die Vertauschungen. Hier müssen im ungünstigsten Fall Vertauschungen in einer quadratischen Größenordnung durchgeführt werden.
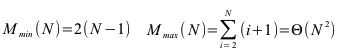
Implementierung
Die Implementierung der Klasse InsertionSort.java ist bei Github zu finden.
- Printer-friendly version
- Log in to post comments
- 14003 views