Der Bubblesort hat seinen Namen von dem Prinzip erhalten, dass der größte Wert eine Folge durch Vertauschungen in der Folge austeigt wie eine Luftblase im Wasser.
Verfahren
- Vergleiche in aufsteigender Folge die Werte einer unsortierten Folge und vertausche die Werte wenn f(i) > f(i+1) ist
- Wiederhole die Vergleiche und eventuell nötige Vertauschungen bis keine Vetauschung bei einem Prüfdurchlauf vorgenommen werden muss.
Beispiel
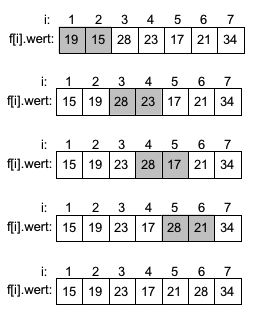 |
Es werden die Werte aufsteigen auf ihre korrekte Reihenfolge verglichen. Im ersten "Durchlauf" müssen die Werte 19 und 15 (in grau) getauscht werden. Anschließend werden die Werte 28 und 23 getauscht und im nächsten Schritt die Werte 28 und 17. Die letzte Vertauschung findet zwischen 28 auf Position 5 und 21 auf Position 6 statt. Der erste Durchlauf ist beendet und der zweite Durchlauf beginnt mit den Vergleichen ab Index 1. |
| Im zweiten Durchlauf sind die Werte auf Index 1 und 2 in der richtigen Reihenfolge. Die Werte 23 und 17 sind die ersten die getauscht werden müssen. Der Wert 23 steigt weiter auf und wird noch mit dem Wert 21 getauscht. Die letzten beiden Werte auf Index 6 und 7 sind in der richtigen Reihenfolge und müssen nicht getauscht werden. Der zweite Durchlauf ist beendet. | 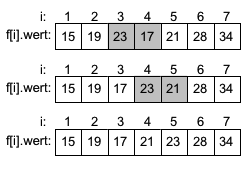 |
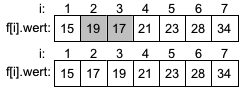 |
Im dritten Durchlauf muß die 19 auf Position 2 mit der 17 auf Position 3 getauscht werden. Auf den höheren Positionen sind keine Veratuschungen mehr nötig. |
Der vierte Durchlauf ist der letzte Durchlauf. In ihm finden keine weiteren Vertauschungen statt. Alle Elemente sind aufsteigend sortiert. Der Algorithmus bricht nach dem vierten Durchlauf ab, da keine Vertauschungen nötig waren. Alle Elemente sind sortiert.
Aufwand
Der günstigste Fall für den Bubblesort ist eine sortierte Folge. In diesem Fall müssen nur N-1 Vergleiche und keine Vertauschungen vorgenommen werden.
Ungünstige Fälle sind fallende Folgen. Findet man das kleinste Element auf dem höchsten Index sind N-1 Durchläufe nötigt bei denen das kleinste Element nur um eine Position nach vorne rückt.
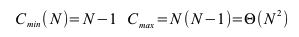
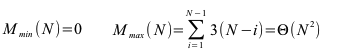
In ungünstigen Fällen ist der Aufwand N2. Man kann zeigen, dass der mittlere Aufwand bei N2 liegt:
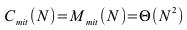
Effizienzsteigerungen
Es gibt eine Reihe von Verbesserungen die darauf beruhen, dass man nicht bei jedem Durchlauf in der ganzen Folge die Nachbarn vergleichen muss. Nach dem ersten Durchlauf ist das größte Element auf dem Index N angekommen. Man muss im nächsten Durchlauf also nur noch alle Nachbarn bis zur Position N-1 kontrollieren.
Implementierung
Die Implementierung der Klasse BubbleSort.java ist bei Github zu finden.
- Printer-friendly version
- Log in to post comments
- 7836 views