Der Quicksort ist ein Verfahren welches auf dem Grundprinzip des rekursiven Teilens basiert:
- Man nimmt ein beliebiges Pivotelement als Referenz (Pivotpunkt: Drehpunkt, Angelpunkt)
- Man teilt die unsortierte Folge in drei Unterfolgen
- Alle Elemente die kleiner oder gleich dem Pivotelement sind
- Das Pivotelement
- Alle Element die größer oder gleich dem Pivotelement sind
Die Unterfolgen die größer bzw. kleiner als das Pivotelement sind, sind selbst noch unsortiert. Das Pivotelement steht bereits an der richtigen Position zwischen den zwei Teilfolgen.
Durch rekursives Sortieren werden auch sie sortiert.
Der Quicksort wurde 1962 von C.A.R. Hoare (Computer Journal) veröffentlicht.
Verfahren
- Folgen die aus keinem oder einem Element bestehen bleiben unverändert.
- Wähle ein Pivotelement p der Folge F und teile die Folge in Teilfolgen F1 und F2 derart das gilt:
- F1 enhält nur Elemente von F ohne das Pivotelement p die kleiner oder gleich p sind
- F2 enhält nur Elemente von F ohne das Pivotelement p die größer oder gleich p sind
- Die Folgen F1 und F2 werden rekursiv nach dem gleichen Prinzip sortiert
- Die Ergebnis der Sortierung ist eine Aneinanderreihung der der Teilfolgen F1, p, F2.
Anmerkung: Der Quicksort folgt dem allgemeinen Prinzip von "Teile und herrsche" (lat.: "Divide et impera", engl. "Divide and conquer")
Beispiel
Im ersten Schritt wird das vollständige Feld vom Index 1 bis 7 sortiert, indem der Wert 23 auf dem Index 7 als Pivotwert (Vergleichswert) gewählt.
Es wird nun vom linken Ende des Intervals (Index 1) aufsteigend das erste Element gesucht welches größer als das Pivotelement ist. Hier ist es der Wert 39 auf dem Index 2. Anschließend wird vom oberen Ende des Intervals von der Position links vom Pivotelement absteigend das erste Element gesucht welches kleiner als das Pivotelement ist. Hier ist es der Wert 19 auf dem Index 6.
Im nächsten Schritt werden die beiden gefundenen Werte getauscht und liegen nun in der "richtigen" Teilfolge.
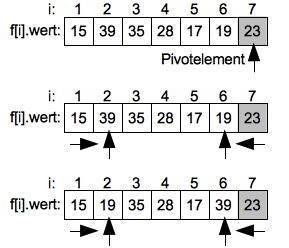
Jetzt wird die Suche von links nach rechts weitergeführt bis das nächste Element gefunden ist welches größer als das Pivotelement ist. Hier ist es 35 auf Position 3. Die fallende Suche von Rechts endet bei dem Wert 17 auf Index 5. Die beiden Werte werden dann getauscht.
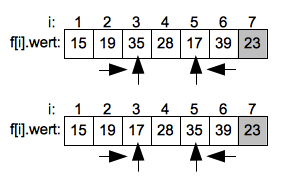
Nach der Vertauschung wird die aufsteigende Suche von Links weitergeführt und endet beim Wert 28 auf dem Index 4. Die fallende Suche von Rechts endet sofort da der Suchindex der steigenden Suche erreicht ist.
Der Pivotwert 23 auf Index 7 wird jetzt mit 28 auf dem Index getauscht und hat seine korrekte Endposition erreicht.
Der Sortiervorgang wird jetzt rekursiv im Intervall 1 bis 3 und 5 bis 7 fortgeführt. Wie zuvor werden die Werte auf dem höchsten Index der Unterintervalle wieder als Pivotwerte gewählt.
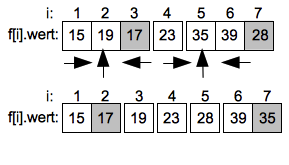
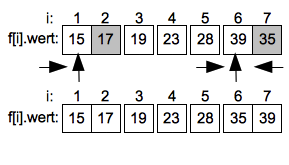
Im linken Unterintervall endet die aufsteigende Suche schnell beim Wert 19 auf Index 2 der dann mit dem Pivotwert 17 getauscht wird. Im rechten Unterintervall muss bei der aufsteigenden suche der Wert 35 auf Index 5 mit dem Pivotwert 28 getauscht werden.
Bei den weiteren Teilungen in Unterintervalle bleiben nur noch das Intervall von Index 1 bis 2 sowie das Intervall von Index 6 bis 7 übrig. Hier werden wieder die Elemente am rechten Rand als Pivotwerte gewählt.
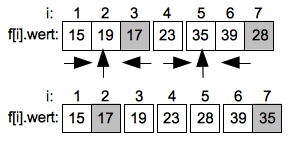
Im linken Unterintervall durchläuft die aufsteigende Suche das einzige Element und endet ohne Vertauschung. Im rechten Intervall muss ein letztes mal der Wert 39 mit 35 getauscht werden.
Aufwand
Der Quicksort ist in normalen Situationen mit einem Aufwand von n*log(n) sehr gut für große Datenmengen geeignet. Er ist einer der schnellsten Algorithmen. Bei sehr ungünstigen Sortierfolgen (schon sortiert) kann er aber auch mit einem quadratischen Aufwand sehr ineffizient sein.
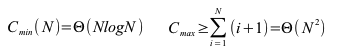
Vorsortierte Folgen sind durchaus häufig bei realen Problemen zu finden. Der Quicksort ist bei schon sortierten Folgen sehr ineffizient ist und daher ist der Einsatz bei realen Anwendungen durchaus heikel.
Implementierung
Serieller Quicksort
Die Implementierung der Klasse QuickSort.java ist bei Github zu finden.
Parallelisierter Quicksort
Die unten aufgeführte Klasse nutzt die "Concurrency Utilities" die in Java 7 eingeführt wurden. Aus der Sammlung wird das Fork/JoinFramework verwendet. Die Implementierung der Klasse QuickSortParallel.java ist bei Github zu finden.
Das Aufteilen des Sortierintervalls erfolgt hier seriell in einer eigenen Methode.
Das Sortieren der Teilintervalle erfolgt parallel solange das Intervall eine bestimmte Mindestgröße (100) besitzt.
Die Fork/Join Klassen stellen dem Algorithmus einen Pool von Threads zur Verfügung die sich nach der Anzahl des Prozessoren des Rechners richten.
Hierzu dient eine Spezialisierung der Klasse RecursiveAction.
- Die Methode compute() wird in einem eigenen Thread durchgeführt wenn das dazugehörige Objekt mit der Methode invokeAll()aufgerufen wird. Diese Methode wird überschrieben.
- Die Methode invokeAll() erlaubt es neue Tasks zu in Auftrag zu geben. Diese Methode wird erst beendet wenn alle Tasks ausgeführt sind.
In der vorliegenden Implementierung erfolgt ein paralleler Aufruf eines Task zum Sortieren der Teilintervalle und nicht ein sequentieller Methodenaufruf.
Die Implementierung des Task erfolgt in der inneren Klasse Sorttask. Diese Klasse ummantelt quasi die Sortiermethode.
- Printer-friendly version
- Log in to post comments
- 13270 views
Verfahren
Im Abschnitt "Verfahren" wird das Pivotelement zuerst "p" genannt. Im weiteren Verlauf wird jedoch "k" als Pivotelement bezeichnet. Richtig müsste es aber auch "p" heißen, oder?
Folgen die aus keinem oder einem Element bestehen bleiben unverändert.
Wähle ein Pivotelement p der Folge F und teile die Folge in Teilfolgen F1 und F2 derart das gilt:
F1 enhält nur Elemente von F ohne das Pivotelement k die kleiner oder gleich k sind
F2 enhält nur Elemente von F ohne das Pivotelement k die größer oder gleich k sind
Die Folgen F1 und F2 werden rekursiv nach dem gleichen Prinzip sortiert
Die Ergebnis der Sortierung ist eine Aneinanderreihung der der Teilfolgen F1, k, F2.
Stimmt!
Danke für den Hinweis. Ich habe das Skript auf p geändert,
typo
Beispiel
[...](nach dem zweiten Bild)
Der Pivotwert 23 auf Index 7 wird jetzt mit 28 auf dem Index getauscht und hat seine korrekte Endposition erreicht.
[...]
Aufwand
Der Quicksort ist in normalen Situationen mit einem Aufwand von n*log(n) sehr gut für große Datenmengen geeignet. Er ist einer der schnellsten Algorithmen. Bei sehr ungünstigen Sortierfolgen (schon sortiert) kann er aber auch mit einem quadratischen Aufwand sehr ineffizient sein.
Danke
Wurde verbessert.
Verfahren (Intervallbildung)
Sie beschreiben das Ergebnis des Teilsortierverfahres als eine Aneinanderreihung von F1, p, F2 (also quasi 3 Intervalle).
Nachdem 17 aber in dem linken Teilintervall als Pivotelement für die weitere Ausführung verwendet wird, ist 17 also p kein eigenes Teilintervall sondern laut ihrer Darstellung Teil des Intervalls 15,17. Wie kommt das?
Sehr gut beobachtet
Das Pivotelement kann ein kleines Intervall bilden. Es steht halt zwischen den beiden großen Intervallen. Schlechte Erklärung meiner Seite.
Ein Gedankenexperiment:
* Ein anderes Element kann den gleichen Schlüssel wie das Pivotelement haben. Das wurde in den Beispielen nie durchgespielt...
* Gleich ob man mit ,>= tested, das andere Element gehört zum Intervall links oder rechts.
* Deswegen sollte auch das Pivotelement so behandelt werden. Es gehört in das linke oder rechte Intervall.
* Das mittlere Intervall macht nicht richtig Sinn.
Das dritte Intervall macht auch keinen Unterschied bei der Komplexität des Algorithmus. Es ist sehr klein im vergleich zu den beiden anderen Intervallen. Ich würde es als eine Variante akzeptieren.