Übungen (Sortieren)

Teamübung: Analyse und Implementierung eines Sortieralgorithmus

Wählen Sie einen Algorithmus

  • recherchieren Sie seine Funktion
  • implementieren Sie den Algorithmus

1. Konfiguration der Laufzeitumgebung

Benutzen Sie die Beispielprogramme zum Sortieren:

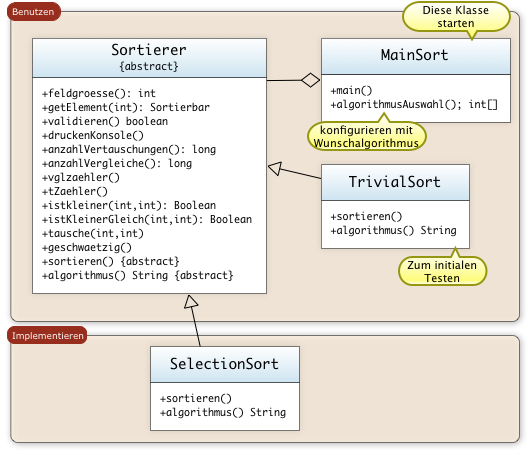
  • Kopieren Sie sich die Klassen Sortierer, MainSort auf ihr System
  • Kopieren Sie sich die Klasse SelectionSort auf Ihr System
  • "Aktivieren" Sie sich den gewünschten Sortieralgorithmus in der Klasse MainSort, Methode algorithmusAuswahl(). Alle Sortieralgorithmen sind als Kommentarzeilen vorhanden. Das Entfernen genau eines Kommentar's aktiviert den gewünschten Algorithmus. Beginnen Sie zum Testen mit der Referenzimplementierung der Klasse SelectionSort.

Testen Sie die Gesamtanwendung durch das Aufrufen des Hauptprogramms MainSort.

In diesem Fall beginnt das Programm ein kleines Feld zu sortieren und gibt die Anzahl der Vergleiche, Vertauschungen, Größe des Feldes und die benötigte Zeit in Millisekunden aus. Dies ist die Phase 1. Wurde das kleine Feld erfolgreich sortiert beginnt Phase 2. Hier wird die Feldgröße jeweils verdoppelt. Das Programm bricht ab nachdem zum ersten Mal eine Zeitgrenze (3 Sekunden) beim Sortieren überschritten wurde. Hiermit lässt sich die Effizienz des Algorithmus testen und die Komplexitätsabschätzungen kontrollieren.

2. Implementieren Sie den neuen Sortieralgorithmus

Orientieren Sie sich am Beispiel der Klasse SelectionSort

  • Erzeugen Sie eine neue Klasse, die aus der Klasse Sortierer abgeleitet wird
  • Implementieren sie einen einfachen Konstruktor der das übergebene Feld an die Oberklasse Sortierer weiterreicht: 
    • public XYSort(Sortierbar[] s) {super(s);}
  • Implementieren Sie eine Methode mit dem Namen algorithmus() die den Namen des Algorithmus ausgibt 
    • public String algorithmus() {return "XYsort";}
  • Implementieren Sie den eigentlichen Sortieralgorithmus in der Methode public void sortieren(anfang, ende)
    • Diese Methode soll als Ergebnis alle Elemente von der Position anfang im Feld bis zum Feldelement ende aufsteigend sortiert haben.

 2.1 Infrastruktur für die Methode sortieren(anfang, ende)

Die Oberklasse Sortierer stellt alles zur Verfügung was man zum Sortieren benötigt

  • tausche(x,y) erlaubt das Tauschen zweier Feldelemente auf der Position x mit dem Element auf der Position y
  • boolean istKleiner(x,y) gibt den Wert true (wahr) zurück wenn der Inhalt der Feldposition x kleiner als der Inhalt der Feldposition y ist

Diese beiden Hilfsmethoden sind die einzigen Methoden die zum Implementieren benötigt werden. Der Typ des zu sortierenden Feldes bleibt hinter dem Interface Sortierbar verborgen. Im vorliegenden Fall sind es ganze Zahlen.

Um die Entwicklung zu Vereinfachen bietet die abstrakte Klasse Sortieren eine Reihe von Hilfsmethoden:

  • druckenKonsole(): druckt das gesamt Feld mit seiner Belegung auf der Konsole aus
  • generiereZufallsbelegung(): Belegt ein existierendes Feld mit neuen Testdaten 
  • long anzahlVertauschungen(): Gibt die Zahl der Vertauschungen an. Sie werden durch Aufrufe von tausche() gezählt
  • long anzahl Vergleiche(): Gibt die Zahl der Vergleiche aus. Sie werden durch Aufrufe von istKleiner() gezählt
  • boolean validierung(): Erlaubt die Prüfung eines sortierten Felds. Der Wert ist wahr wenn das Feld korrekt sortiert ist.

3. Anpassen des Hauptprogramms MainSort

Das Hauptprogramm MainSort erzeugt an einer Stelle eine Instanz der Klasse SelectionSort. Ändern Sie diese Stelle im Programm derart, dass eine Instanz Ihrer neuen Sortierklasse aufgerufen wird.

4. Vorbereitende Tests für die Präsentation

Ändern Sie die zu sortierenden Testdaten im Programm MainSort derart ab, dass Sie

  • den ungünstigsten Fall für den Sortieralgorithmus wählen (Vertauschungen, Prüfungen)
  • den günstigsten Fall wählen (Vertauschungen, Prüfungen)

Tragen Sie die abgelesen Werte in eine Tabellenkalkulation ein und prüfen Sie ob die Aufwände mit den Vorhersagen des Lehrbuchs übereinstimmen (Grafiken!)

Bereiten Sie eine 15-20 minütige Vorstellung/Präsentation des Algorithmus vor:

  • Erklären des Algorithmus (mit Beispiel)
    • Tafel, Folie, Overheadprojektor genügen
  • Vorführen einer Implementierung
  • Komplexitätsüberlegungen und Bewertung
    • Was ist der durchschnittliche Aufwand?
    • Was ist der minimale Aufwand (Beispiel)?
      • Wählen Sie die Anzahl der Vertauschungen oder der Vergleiche
    • Was ist der Aufwand im ungünstigsten Fall (Beispiel)?
      • Wählen Sie die Anzahl der Vertauschungen oder der Vergleiche
  • Wichtige Punkte die abhängig vom Algorithmus beachtet werden sollen
    • Sortieren durch Auswahl
      • Präsentation
        • Erklären Sie die "Sortiergrenze"
    • Bubblesort
      • Präsentation
        • Welche Elemente werden immer vertauscht?
        • Warum ist diese Strategie intuitiv aber nicht effizient?
    • Quicksort
      • Nutzen Sie Bleistifte oder Streichhölzer zum Visualieren des Verfahrens.
      • Legen Sie das Pivotelement in Ihrer Implementierung der Einfachheit halber an eine feste Intervallgrenze!
      • Algorithmus:
        • Erklären Sie das grundlegende Konzept des Quicksorts (3 Sätze reichen hier!)
        • Erklären Sie die Rekursion (Teile und Herrsche) und das Ende der Rekursion (Abbruch)
      • Implementierung
        • Erklären Sie den Begriff des "Pivotelement"
        • Die Implementierung ist durchaus kompliziert. Skizieren Sie sie nur.
    • Heapsort
      • Diskutieren Sie den Dualismus der beiden Zugriffstrukturen
        • Sie arbeiten auf einem Feld (Array)
        • Sie betrachten auf der abstrakten Ebene einen Baum
        • Wie ist der Zusammenhang zwischen Blattknoten und Feldpositionen?
      • Implementierung
        • Schreiben Sie Methoden zur Bestimmung der linken und rechten Blattknoten
        • Schreiben Sie eine Methode zum Versickern
      • Präsentation
        • Erläutern Sie den Dualismus
        • Erläutern Sie die Bestimmung der Blattknoten
        • Erläutern Sie die "Heapbedingung"
          • Wie wird sie hergestellt
        • Erläutern Sie das Konzept des "Versickerns" 
    • Referenzen aus dem Internet
      • Zeigen die Referenzen, die Sie am besten mögen: Lustig, lehrreich, witzig
    • Zusammenfassung:
      • Wie mögen Sie den Algorithmus?
      • Wie aufwendig war die Implementierung?