Herstellen der Heapbedingung
Top-Down-Verfahren
Dieses Verfahren dient der Herstellen der Heapbedingung, wenn schon für die Unterheaps für die Heapbedingung gilt.
Man wendet es an, nachdem man den größten Schlüssel entnommen hat und ihn durch den Wert mit dem größten Index im unsortierten Baum ersetzt hat.
Das Versickern dieses neuen Schlüssels an der Wurzel des Baums erfolgt mit den folgenden Schritten:
- Beginne mit der Position i=1 im Baum
- Der Schlüssel f[i] hat keine Unterknoten da 2*i>N ist,
- Der Schlüssel kann nicht mehr versickert werden. Das Verfahren ist beendet.
- Der Schlüssel f[i] hat noch genau einen Unterknoten f[i*2]
- Der Schlüssel f[i] wird mit dem Schlüssel f[i*2] getauscht falls f[i]<f[i*2]. Das Verfahren ist nach diesem Schritt beendet.
- Der Schlüssel f[i] hat noch Unterknoten f[2*i] und f[2*i+1]
- Der Schlüssel f[i] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Das Verfahren ist beendet die Heapbedingung ist gegeben
- Der Schlüssel f[i*2] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Tausche die Schlüssel f[i] mit f[2*i]
- Versickere den Schlüssel f[i*2] nach dem Top-Down Verfahren
- Der Schlüssel f[i*2+1] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Tausche die Schlüssel f[i] mit f[2*i+1]
- Versickere den Schlüssel f[i*2+1] nach dem Top-Down Verfahren
- Der Schlüssel f[i] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
Diese rekursive Verfahren wird hier an einem Beispiel gezeigt:
| Grafische Visualisierung | Beschreibung |
|---|---|
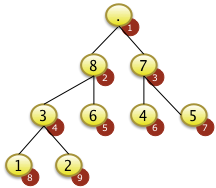 |
Durch das Entfernen des größten Schlüssels f[1] entstehen zwei Unterbäume für die die Heapbedingung nach wie vor gilt. |
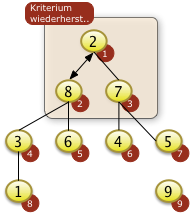 |
Durch das Einsetzen eines Schlüssel von der Position N ist nicht mehr garantiert, dass die Heapbedingung für den gesamten Restbaum f[1] bis f[N-1]=f[8] gegeben ist. Der Schlüssel f[1]=2 ist eventuell größer als die Schlüssel f[2*1] und f[2*1+1]. In diesem Fall ist die Heapbedingung für f[1] bis f[8] schon gegeben. Es muss nichts mehr getan werden. Im vorliegenden Fall ist f[1]=2 aber nicht der größte Schlüssel. Er muss rekursiv versickert werden. Dies geschieht durch das Vertauschen mit f[2] = 8. f[3] = 7 ist nicht der richtige Kandidat. 7 ist nicht der größte der drei Schlüssel. |
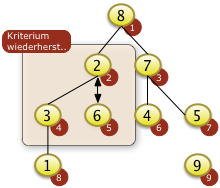 |
Nach dem Vertauschen von f[1] mit f[2] gilt die Heapbedingung zwar für den obersten Knoten. Sie gilt jedoch nicht für den Teilbaum unter f[2]= 2. Der Schlüssel 2 muss weiter versickert werden. In diesem Fall ist f[5]=6 der größte Schlüssel mit dem f[2]= 2 vertauscht weden muss. |
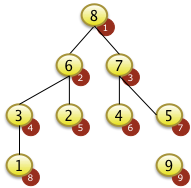 |
Nach dem Vertauschen von f[2] mit f[5] gilt die Heapbedingung wieder für den gesamten Baum. |
- Printer-friendly version
- Log in to post comments
- 6959 views
Der Satz "Man wendet es an,
Der Satz "Man wendet es an, nachdem man den größten Schlüssel entnommen hat und ihn durch einen zufälligen Wert ersetzt hat." ist missverständlich formuliert.
Der Wert wird nicht zufällig ausgewählt, sondern ist der letzte im Baum verbliebene Knoten.
Stimmt. Danke
wurde verbessert.
Im Schritt 2 ist auch wieder
Im Schritt 2 ist auch wieder das "zufällig" irreführend, da der Wert ja nicht aus der Luft gezaubert wird, sondern von/auf Position N vorgegeben ist. (Ob die Werte des Heaps zufällig erstellt wurden, ist hier ja nicht von Bedeutung.)
( + typo )
"Durch das Einsetzen eines
zufälligenSchlüssels von der Position N ist nicht mehr garantiert, dass die Heapbedingung für den gesamten Restbaum f[1] bis f[N-1]=f[8] gegeben ist."Macht Sinn
Gutes Feedback. Habe das Wort "zufällig" entfernt.
Dieses Verfahren dient der Herstellen der Heapbedingung wenn sch
Sollte geändert werden in: "Dieses Verfahren dient dem Herstellen der Heapbedingung, wenn schon für Unterheaps die Heapbedingung gilt."
Danke, für das Feedback
Das Kommando habe ich eingefügt. Der Artikel "die" habe ich gelassen.