Binärbäume werden benutzt da sie ein sehr effizientes Suchen mit einem Aufwand von O(logN) erlauben solange sie balanciert sind. In extremen Fällen kann die Suche nach Knoten jedoch zu einem Aufwand von O(N) führen falls der Baum degeneriert ist.
Die im vorhergehenden Abschnitt vorgestellten Bäume verwenden in ihren Implementierungen der Einfüge- und Entferneoperation naive Verfahren. Diese naive Verfahren können dazu führen, dass ein Baum sehr unbalanciert werden kann.
Erste Vorschläge zur Vermeidung dieses Problems gehen auf die 1962 gemachten Vorschläge von Adelson-Velskij und Landis zurück. Sie schlugen höhenbalancierte AVL Bäume vor.
AVL Bäume
| AVL Baum |
|---|
|
Ein binärer Baum ist höhenbalanciert bzw AVL ausgeglichen wenn für jeden Knoten im Baum gilt:
|
Beispiele von AVL Bäumen die der obigen Definition genügen sind im folgenden Diagramm zu sehen
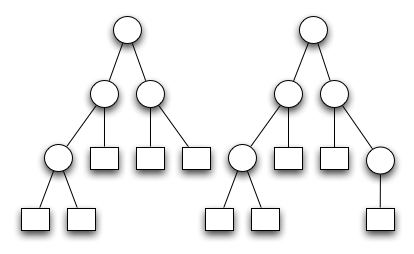
Der nachfolgende Baum ist kein AVL Baum. Der rechte Knoten in der zweiten Ebene von oben hat einen linken Unterbaum der Höhe 1 und einen rechten Unterbaum der Höhe 3.
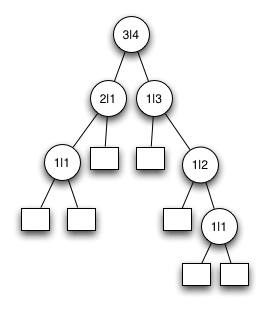
Dieser Baum müsste umorganisiert werden um ein AVL Baum zu werden.
Zum Verwalten von AVL Bäumen berechet man jedoch nicht immer wieder die Höhe der Teilbäume.
Es ist einfacher einen Balanchefaktor zu jedem inneren Knoten mitzuführen der die Differenz der Höhe vom linken und rechtem Teilbaum verwaltet.
| Balancefaktor bal(p) eines AVL Baums |
|---|
|
bal(p) = (Höhe rechter Teilbaum von p) - (Höhe linker Teilbaum von p) bal(p)∈{-1,0,1} |
Im folgenden Beispiel sind die Balancefaktoren für die inneren Knoten eingetragen:
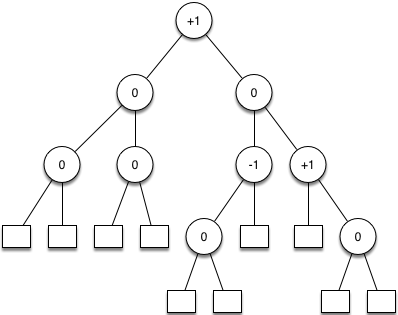
AVL Bäume müssen beim Einfügen und Entfernen von Knoten unter Umständen neu balanciert werden. Der Vorteil besteht jedoch in dem sehr vorhersagbaren Verhalten mit dem Aufwand von O(logN) bei Operationen auf dem Baum.
Tipp: Bauen Sie sich Ihren eigen AVL Baum. Die Universität hat eine web basierte Visualisierung von AVL Bäumen.
- Printer-friendly version
- Log in to post comments
- 12067 views
Definition AVL-Baum, 2. Abb.
Kann es sein, dass bei den korrekten AVL-Bäumen unten rechts ein Kästchen fehlt? Dort ist bei einem Kreis lediglich ein Kästchen.
Hmm, nein
sehr genau hingeschaut. Dies ist ein Knoten der nur einen Unterknoten hat. Das ist an dieser Stelle OK. Die Prüfung ist die folgende: Blattknoten (Endknoten) dürfen sich in ihrer Höhe nur um maximal eine Ebene unterscheiden.