Balancierte und unbalancierte Bäume
Das folgende Programm erlaubt es manuell einen streng geordneten Binärbaum aus Ganzzahlen aufzubauen.
Das Programm steht als jar Datei zur Verfügung und kann nach dem Download wie folgt gestartet werden:
java -jar BaumGUI.jar
Balancierter Baum
Benutzen Sie das Beispielprogramm und erzeugen sie einen balancierten Baum mit 15 Knoten und der Höhe 4 wie zum Bsp.:
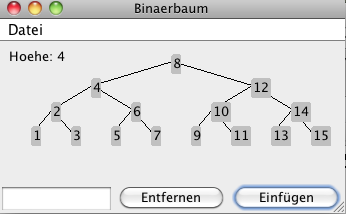
In welcher Reihenfolge müssen die Werte eingegeben werden?
Degenerierter Baum
Erzeugen Sie einen degenerierten Baum mit 5 Knoten und der Höhe 5:
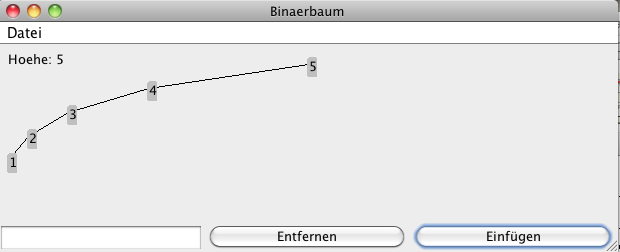
Welche Eingabefolgen von Zahlen erzeugen eine Liste degenerierten Teilbäumen?
Implementierung einer Binärbaums
Alle Klassen zu dieser Übung sind auch über github verfügbar.
Implementieren Sie einen streng geordneten Binärbaum in dem man ganze Zahlen Einfügen und Löschen kann.
Es ist nicht notwendig einen balancierten Baum oder AVL Baum zu implementieren.
Vervollständigen Sie die 3 drei fehlenden Methoden:
- s2.baum.Baumknoten
- Methode hoehe() : Implementieren Sie eine rekursive Methode zum bestimmen der Höhe des Baums (1.ter Schritt)
- s2.baum.Binaerbaum
- Methode einfuegen(teilBaum, Knoten) (2.ter Schritt)
- Tipps
- Betrachten Sie zuerst Sonderfälle (fehlen von Söhnen)
- Welchen Teilbaum müssen Sie modifizieren wenn der neue Knoten kleiner als die aktuelle Wurzel ist?
- Welchen Teilbaum müssen Sie modifizieren wenn der neue Knoten größer als die aktuelle Wurzel ist?
- Fügen Sie keinen Knoten mit einem Wert ein, der schon existiert!
- Tipps
- Methode loeschen(teilBaum, Knoten) (3.ter Schritt)
- Tipps
- Was müssen Sie tun wen der aktuelle Knoten gelöscht werden muss?
- Was müssen Sie tun wenn der zu löschende Knoten die Wurzel des gesamten Baums ist?
- Tipps
- Methode einfuegen(teilBaum, Knoten) (2.ter Schritt)
Übersetzen Sie alle Klassen. Starten Sie die Anwendung mit
$ java s2.baum.BaumGUI
Testen Sie die Anwendung mit der automatisierten Generierung mit dem Befehl
$ java s2.baum.BaumGUI magic
Hinweis: Die Implementierung des Algorithmus zum Entfernen von Knoten ist sehr viel aufwendiger da viele Randbedingungen geprüft werden müssen. Implementieren Sie zu Beginn nur das Einfügen von Knoten und Testen Sie zuerst das Einfügen. Die aktuelle Trivialimplementierung zum Entfernen erlaubt das Übersetzen und Ausführen der Anwendung ohne das Knoten entfernt werden.
UML Diagramm der beteiligten Klassen:
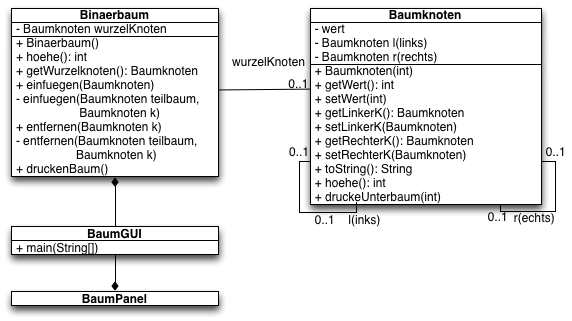
Notwendige Vorarbeiten
Erzeugen Sie die Infrastruktur für das folgenden Paket s2.baum
Klasse s2.baum.Baumknoten
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class Baumknoten {
private int wert;
//private final int maxWert= Integer.MAX_VALUE;
private final int maxWert= 99;
public int getWert() {
return wert;
}
public void setWert(int wert) {
this.wert = wert;
}
/**
* Verwalte linken Knoten
*/
private Baumknoten l;
/**
* verwalte rechten Knoten
*/
private Baumknoten r;
public Baumknoten(int i) {wert=i;}
/**
* Liefere linken Knoten zurück
* @return linker Knoten
*/
public Baumknoten getLinkerK() {
return l;
}
/**
* Setze linken Knoten
* @param k Referenz auf linken Knoten
*/
public void setLinkerK(Baumknoten k) {
l = k;
}
/**
* Liefere rechten Knoten zurück
* @return rechter Knoten
*/
public Baumknoten getRechterK() {
return r;
}
/**
* Setze rechten Knoten
* @param k rechter Knoten
*/
public void setRechterK(Baumknoten k) {
r = k;
}
/**
* Drucken einen Unterbaum und rücke entsprechend bei Unterbäumen ein
* @param einruecken
*/
public void druckeUnterbaum(int einruecken) {
if (l != null) {
l.druckeUnterbaum(einruecken + 1);
}
for (int i = 0; i < einruecken; i++) {
System.out.print(".");
}
System.out.println(toString());
if (r != null) {
r.druckeUnterbaum(einruecken + 1);
}
}
/**
* Berechne Höhe des Baums durch rekursive Tiefensuche
* @return
*/
public int hoehe() {
System.out.println("Implementieren Sie Baumknoten.hoehe() als rekursive Methode");
return -1;
}
/**
* Generiere eine Zufallsbelegung für den gegebenen Knoten
* Die Funktion darf nicht mehr nach Einfügen in den Baum
* aufgerufen werden, da der neue Wert zu einer inkorrekten Ordnung führt
*/
public void generiereZufallswert() {
wert= (int)(Math.random()*(double)maxWert);
}
/**
* Erlaubt den Zahlenwert als Text auszudrucken
* @return
*/
public String toString() { return Integer.toString(wert);}
}
Klasse s2.baum.Binaerbaum
package s2.baum;
/**
*
* @author sschneid
*/
public class Binaerbaum {
private Baumknoten wurzelKnoten;
public Baumknoten getWurzelknoten() {return wurzelKnoten;}
/**
* Füge einen neuen Baumknoten in einen Baum ein
* @param s
*/
public void einfuegen(Baumknoten s) {
if (wurzelKnoten == null) {
// Der Baum ist leer. Füge Wurzelknoten ein.
wurzelKnoten = s;
}
else // Der Baum ist nicht leer. Normales Vorgehen
einfuegen(wurzelKnoten,s);
}
/**
* Füge einen gegebenen Knoten s in einen Teilbaum ein.
* Diese Methode ist eine rekursive private Methode
* Da der neue Knoten die Wurzel des neuen Teilbaums bilden kann,
* wird eventuell ein Zeiger auf einen neuen Teilbaum zurückgeliefert
* Randbedingung:
* * Es wird kein Knoten mit einem Wert eingefügt der schon existiertz
* @param teilbaum
* @param s
*/
private void einfuegen(Baumknoten teilbaum, Baumknoten s) {
System.out.println("Implementieren Sie die Methode Binaerbaum:einfuegen()");
}
/**
* Öffentliche Methoden zum Entfernen eines Baumknotens
* @param s
*/
public void entfernen(Baumknoten s) {
wurzelKnoten = entfernen(wurzelKnoten,s);}
/**
* Private, rekursive Methode zum Entfernen eines Knotens aus einem
* Teilbaum. Es kann ein neuer Teilbaum enstehen wennn der Wurzelknoten
* selbst entfernt werden muss. Der neue Teilbaum wird daher wieder mit
* ausgegeben
* @param teilbaum Teilbaum aus dem ein Knoten entfernt werden soll
* @param s der zu entfernende Knoten
* @return Der verbleibende Restbaum. Es kann auch Null für einen leeren Baum ausgegeben werden
*/
private Baumknoten entfernen(Baumknoten teilbaum, Baumknoten s) {
System.out.println("Implementieren Sie die Methode Binaerbaum:entfernen()");
return teilbaum;
}
/**
* Berechnung der Hoehe des Baums
* @return Hoehe des Baums
*/
public int hoehe() {
if (wurzelKnoten == null) return 0;
else return wurzelKnoten.hoehe();
}
/**
* Rückgabe des Namens
* @return
*/
public String algorithmus() {return "Binaerbaum";}
public void druckenBaum() {
System.out.println("Tiefe:" + hoehe());
if (wurzelKnoten != null) wurzelKnoten.druckeUnterbaum(0);
System.out.println("A-----------A");
}
}
Klasse s2.baum.BaumGUI
package s2.baum;
import java.awt.BorderLayout;
import java.awt.Container;
import java.awt.GridLayout;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JMenu;
import javax.swing.JMenuBar;
import javax.swing.JMenuItem;
import javax.swing.JPanel;
import javax.swing.JTextField;
/**
*
* @author s@scalingbits.com
*/
public class BaumGUI implements ActionListener {
final private JFrame hf;
final private JButton einfButton;
final private JButton entfButton;
final private JTextField eingabeText;
final private JMenuBar jmb;
final private JMenu jm;
final private JMenuItem exitItem;
final private BaumPanel myBaum;
final private Binaerbaum b;
public BaumGUI(Binaerbaum bb) {
b = bb;
JLabel logo;
//ButtonGroup buttonGroup1;
JPanel buttonPanel;
// Erzeugen einer neuen Instanz eines Swingfensters
hf = new JFrame("BaumGUI");
// Gewünschte Größe setzen
// 1. Parameter: horizontale Größe in Pixel
// 2. Parameter: vertikale Größe
hf.setSize(220, 230);
// Beenden bei Schliesen des Fenster
hf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
// Erzeugen der Buttons und Texteingabefeld
eingabeText = new JTextField("17");
einfButton = new JButton();
einfButton.setText("Einfügen");
entfButton = new JButton();
entfButton.setText("Entfernen");
// Registriere die eigene Instanz
// zum Reagieren auf eine Aktion der beiden Buttons
einfButton.addActionListener(this);
entfButton.addActionListener(this);
// Einfügen der drei Komponenten in ein Panel
// Das Gridlayout führt zum Strecken der drei Komponenten
buttonPanel = new JPanel(new GridLayout(1, 1));
buttonPanel.add(eingabeText);
buttonPanel.add(entfButton);
buttonPanel.add(einfButton);
// Erzeugen des Panels zum Malen des Baums
myBaum = new BaumPanel(b);
// setze Titel des Frame
hf.setTitle(b.algorithmus());
// Erzeuge ein Menueeintrag zum Beenden des Programms
jmb = new JMenuBar();
jm = new JMenu("Datei");
exitItem = new JMenuItem("Beenden");
exitItem.addActionListener(this);
jm.add(exitItem);
jmb.add(jm);
hf.setJMenuBar(jmb);
Container myPane = hf.getContentPane();
myPane.add(myBaum, BorderLayout.CENTER);
myPane.add(buttonPanel, BorderLayout.SOUTH);
hf.pack();
hf.setVisible(true);
hf.setAlwaysOnTop(true);
}
/**
* Diese Methode wird bei allen Aktionen der Menüleiste oder
* der Buttons aufgerufen
* @param e
*/
public void actionPerformed(ActionEvent e) {
Object source = e.getSource();
int wert = 0;
try {
if (source == entfButton) { //Entfernen aufgerufen
wert = Integer.parseInt(eingabeText.getText());
b.entfernen(new Baumknoten(wert));
myBaum.fehlerText("");
myBaum.repaint();
eingabeText.setText("");
}
if (source == einfButton) { // Einfügen aufgerufen
wert = Integer.parseInt(eingabeText.getText());
b.einfuegen(new Baumknoten(wert));
myBaum.fehlerText("");
myBaum.repaint();
eingabeText.setText("");
}
if (source == exitItem) { // Beenden aufgerufen
System.exit(0);
}
} catch (java.lang.NumberFormatException ex) {
// Fehlerbehandlung bei fehlerhafter Eingabe
myBaum.fehlerText("Eingabe '" + eingabeText.getText() + "' ist keine Ganzzahl");
myBaum.repaint();
eingabeText.setText("");
}
}
public static void main(String[] args) {
BaumGUI sg = new BaumGUI(new Binaerbaum());
if ((args.length > 0) && (args[0].equalsIgnoreCase("magic"))) {
sg.magicMode(15);
}
}
public void magicMode(int anzahl) {
Baumknoten[] gz = new Baumknoten[anzahl];
for (int i = 0; i < gz.length; i++) {
gz[i] = new Baumknoten(0);
gz[i].generiereZufallswert();
}
try {
for (int i = gz.length - 1; i >= 0; i--) {
eingabeText.setText(gz[i].toString());
b.einfuegen(gz[i]);
Thread.sleep(800);
myBaum.repaint();
}
for (int i = 0; i < gz.length; i++) {
eingabeText.setText(gz[i].toString());
b.entfernen(gz[i]);
Thread.sleep(800);
myBaum.repaint();
}
} catch (InterruptedException e) {
}
}
}
Klasse s2.baum.BaumPanel
package s2.baum;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import javax.swing.JPanel;
/**
*
* @author s@scalingbits.com
*/
public class BaumPanel extends JPanel{
final private Binaerbaum b;
final private int ziffernBreite = 10 ; // Breite einer Ziffer in Pixel
final private int ziffernHoehe = 20; // Hoehe einer Ziffer in Pixel
private String fehlerString;
public BaumPanel(Binaerbaum derBaum) {
fehlerString = "";
b = derBaum;
setPreferredSize(new Dimension(600,200));
setDoubleBuffered(true);
}
/**
* Setzen des Fehlertexts des Fehlertexts
* @param s String mit Fehlertext
*/
public void fehlerText(String s) {fehlerString = s;}
/**
* Methode die das Panel überlädt mit der Implementierung
* der Baumgraphik
* @param g
*/
public void paintComponent(Graphics g) {
super.paintComponent(g);
int maxWidth = getWidth();
int maxHeight = getHeight();
Baumknoten k = b.getWurzelknoten();
if (k != null) { // Male Wurzelknoten falls existierend
g.setColor(Color.black);
g.drawString("Hoehe: " + b.hoehe(), 10, 20);
g.drawString(fehlerString, 10, 40);
paintKnoten(g,k,getWidth()/2, 20);
}
else {
g.setColor(Color.RED);
g.drawString("Der Baum ist leer. Bitte Wurzelknoten einfügen.",10,20);
}
}
/**
* Malen eines Knotens und seines Unterbaums
* @param g Graphicshandle
* @param k zu malender Knoten
* @param x X Koordinate des Knotens
* @param y Y Koordinate des Knotens
*/
public void paintKnoten(Graphics g,Baumknoten k, int x, int y) {
int xOffset = 1; // offset Box zu Text
int yOffset = 7; // offset Box zu Text
String wertString = k.toString(); // Wert als Text
int breite = wertString.length() * ziffernBreite;
int xNextNodeOffset = ((int)java.lang.Math.pow(2,k.hoehe()-1))*10;
int yNextNodeOffset = ziffernHoehe*6/5; // Vertikaler Offset zur naechsten Kn.ebene
if (k.getLinkerK() != null) {
// Male linken Unterbaum
g.setColor(Color.black); // Schriftfarbe
g.drawLine(x, y, x-xNextNodeOffset, y+yNextNodeOffset);
paintKnoten(g,k.getLinkerK(),x-xNextNodeOffset,y+yNextNodeOffset);
}
if (k.getRechterK() != null) {
// Male rechten Unterbaum
g.setColor(Color.black); // Schriftfarbe
g.drawLine(x, y, x+xNextNodeOffset, y+yNextNodeOffset);
paintKnoten(g,k.getRechterK(),x+xNextNodeOffset,y+yNextNodeOffset );
}
// Unterbäume sind gemalt. Male Knoten
g.setColor(Color.LIGHT_GRAY); // Farbe des Rechtecks im Hintergrund
g.fillRoundRect(x-xOffset, y-yOffset, breite, ziffernHoehe, 3, 3);
g.setColor(Color.black); // Schriftfarbe
g.drawString(wertString, x+xOffset, y+yOffset);
}
}
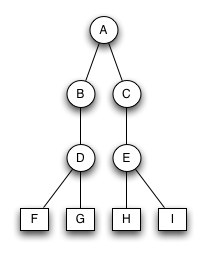
Baumschule...
Fragen zu Binärbäumen
Welche der beiden Bäume sind korrekte, streng sortierte Binärbäume?
Welche sind keine streng sortierten Binärbäume und warum?
Streng sortierter Binärbaum 1
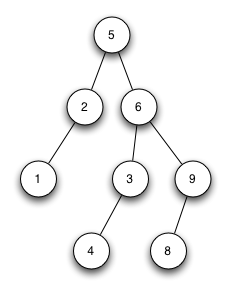
Streng sortierter Binärbaum 2
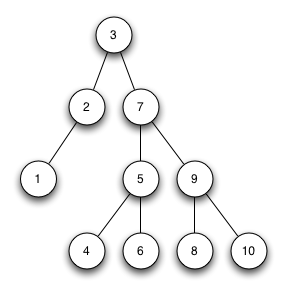
AVL Bäume
Welche der beiden AVL-Bäume sind korrekte AVL-Bäume?
Welche Bäume sind keine korrekten AVL Bäume und warum?
AVL-Baum 1
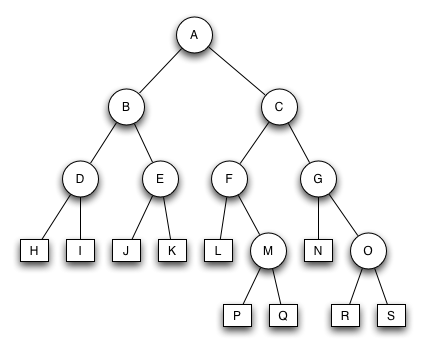
AVL Baum 2
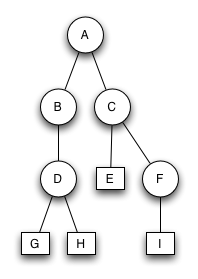
Bruder-Baum
Welche der beiden Bäume sind keine korrekten Bruder-Bäume?
Warum sind sie keine Bruderbäume?
Bruder-Baum 1
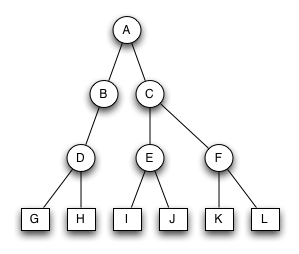
Bruder-Baum 2
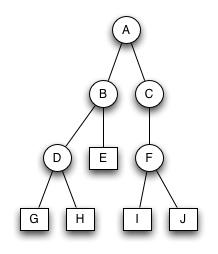
Bruder-Baum 3
- Printer-friendly version
- Log in to post comments
- 12892 views