Bäume werden in vielen Bereichen der Informatik verwendet, da Suchen und Einfügen sehr effizient erfolgen können
| Operation | Erklärung | Aufwand | Schlimmster Fall |
|---|---|---|---|
| Einfügen/Löschen | Ändern des Baums | O(log(n)) | O(n) |
| Suchen | Suchen eines Elements | O(log(n)) | O(n) |
| Nächstes Element | Finden des nächsten Elements | O(1) | O(1) |
Da naiv implementierte Bäume degenerieren können und dann die Aufwände einer Liste haben, werden in der Vorlesung einige, wenige Optimierungen diskutiert. Diese Optimierung unterbinden den schlimmsten Fall eines Aufwands mit der Ordnung O(n).
Bäume sind hierarchische Datenstrukturen die aus einer verzweigten Datenstruktur bestehen. Bäume bestehen aus Knoten und deren Nachfolgern.
Jeder Knoten in einem Baum hat genau einen Vorgängerknoten. Der einzige Knoten für den das nicht gilt, ist der Wurzelknoten (engl. root) er hat keinen Vorgänger. Der Wurzelknoten stellt den obersten Knoten dar. Von dieser Wurzel aus kann man von Knoten zu Knoten zu jedem Element des Baums gelangen.
| Rekursive Definition eines Baums |
|---|
| Ein Baum besteht aus Unterbäumen und diese setzen sich bis zu den Blattknoten wieder aus Unterbäumen zusammen. |
Die Baumstruktur wird in Ebenen unterteilt.
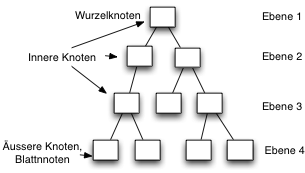
Die Tiefe eines Baumes ergibt sich aus der maximalen Anzahl der Ebenen.
Vollständige Bäume
| Vollständige Bäume |
|---|
| Ein Baum ist vollständig wenn alle Ebenen ausser der letzten Ebene vollständig mit Knoten gefüllt sind. |
Im folgenden Beispiel wird ein Baum gezeigt, der maximal drei Nachfolgerknoten pro Konten besitzen kann:
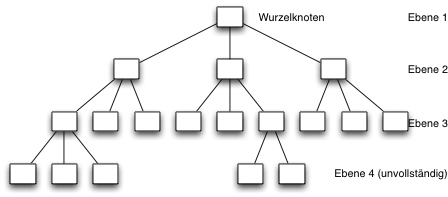
Binärbäume
Binärbäume bestehen aus Knoten mit maximal 2 Nachfolgerknoten. Die maximale Anzahl Knoten pro Ebene ist 2(k-1) Knoten in der Ebene k.
Streng sortierte Binärbäume
| Streng sortierte Binärbäume |
|---|
|
Für jeden Baumknoten gilt:
|
Beispiel eines streng sortierten Binärbaums:
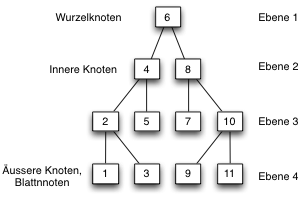
Suchen
Sortierte Binärbäume eignen sich sehr gut zum effektiven Suchen, da mit jedem Knoten die Auswahl der Kandidaten in der Regel halbiert wird.
Das Suchen in einem sortierten Baum geschieht nach dem folgenden, rekursiven Prinzip:
- Beginne mit dem Wurzelknoten
- Vergleiche den gesuchten Wert mit dem Wert des Knoten und beende die Suche wenn der Wert übereinstimmt.
- Suche im linken Teilbaum weiter wenn der gesuchte Wert kleiner als der aktuelle Knoten ist.
- Suche im rechten Teilbaum weiter wenn der gesuchte Wert größer als der Wert des aktuellen Knoten ist.
Bemerkung: Effektives Suchen ist nur in gutartigen (balancierten) Bäumen möglich. Gutartige Bäume haben möglichst wenig Ebenen. Schlechte Bäume zum Suchen sind degenerierte Bäume die im schlimmsten Fall pro Ebene nur einen Knoten besitzen. Solche degenerierten Bäume verhalten sich wie Listen.
Gutartige Bäume haben daher eine Tiefe T= ld(n+a) was auch dem Aufwand zum Suchen O (ld(n)) entspricht. Schlechte Bäume haben eine Tiefe T = n was zu einem Suchaufwand wie bei Listen, also O(n) führt.
Beispielprogramm
|
Das folgende Programm erlaubt es manuell einen Binärbaum aus Ganzzahlen aufzubauen. DownloadDas Programm steht als jar Datei zur Verfügung und kann nach dem Download wie folgt gestartet werden: java -jar BaumGUI.jar Es erlaubt das Einfügen und Entfernen von Blattknoten: |
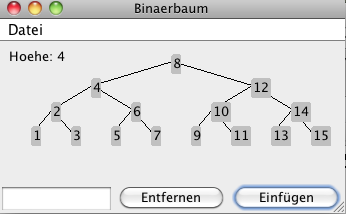 |
Alternative: Die Universität San Francisco hat eine sehr schöne webbasierte Visualisierung.
- Printer-friendly version
- Log in to post comments
- 7931 views