Der BubbleSort besteht aus einer äusseren Schleife in der das zu sortierende Intervall jeweils verkleinert wird.
In einer inneren Schleife wird das größte Element als « Bubble » bestimmt. Führen Sie einen solchen Durchlauf einer inneren Schleife an der unten gezeigten Folge durch. Sortieren sie aufsteigend.
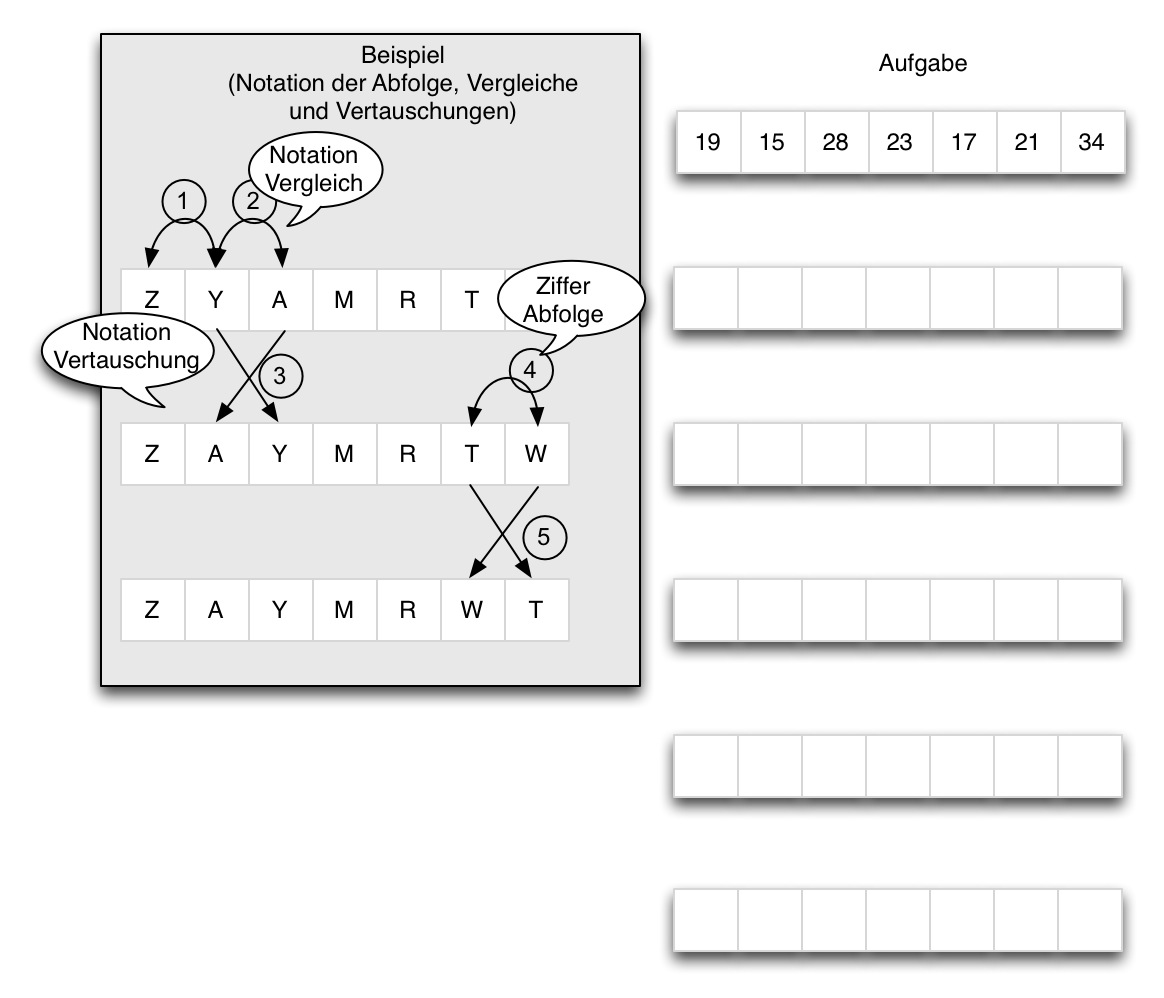
Markieren Sie alle notwendigen Vergleiche und Vertauschungen.
Fügen Sie alle Werte in das Diagramm ein
Welchen Aufwand O() hat der Bubblesort?
In welchem Fall ist ein aufsteigend sortierender Bubblesort ein sehr effizienter Algorithmus?
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 8+1+1 Minuten |
Antwort zu Frage 11: Komplexitätsbetrachtungen 4
| Nr. | Quellcode | Antwort |
|---|---|---|
public class K1 {
private static int groesse = 1000;
public static void main(String[] args) {
algorithmusBsp(groesse);
algorithmus1(groesse);
algorithmus2(groesse);
algorithmus3(groesse);
algorithmus4(groesse);
} |
Nichts in dieses Feld eintragen! | |
| Bsp. |
static void algorithmusBsp(int n) {
for (int i = 1; i < n; i++)
{ int k = i * 2; }
for (int j = 1; j < n; j++)
{ int k = j * 3;}
} |
Beispiel: Ofor1(n)+Ofor2(n) = O(n) |
| 1. |
static void algorithmus1(int n) {
for (int i = 1; i < n; i++) {
int p = n;
for (int j = 1; j < p; j++) {
for (int k = 1; k < n; k++) {
int s = j*k – i;
} // end for
} // end for
} // end for
} |
Ofor1(n)*Ofor2(n)*Ofor3(n) = O(n3) |
| 2. |
static void algorithmus2(int n) {
for (int i = 1; i < n; i++) {
for (int j = 1; j < n; j++) {
int k= 0;
while (k<n) {
k++;
int q = k - j - i;
}
int p=0;
while (p<n) {
p++;
int r = n*p;
} // end while
} // end for
} // end for
} |
Ofor1(n)*Ofor2(n)*(Owhile1(n)+Owhile2(n)) = Ofor1(n)*Ofor2(n)*O(n) = O(n3) |
| 3. |
static void algorithmus3(int n) {
for (int i = 1; i < n; i++) {
for (int j = i; j < n; j++) {
int k=0;
while (k<1000000) {
k++;
int r = i*j*k;
} // end while
} // end for
} // end for
} |
Ofor1(n)*Ofor2(n)*(Owhile1(1000)) = Ofor1(n)*Ofor2(n) = O(n2) |
| 4. |
static void algorithmus4(int n) {
for (int i = 1; i < n; i++) {
for (int j = 1; j < 1000; j++) {
algorithmus1(n);
}
}
} |
Ofor1(n)*Ofor2(1000)*Oalgorithmus1(n) = Ofor1(n)*O(n3) = O(n4) |
}// Ende der Klasse |
--- |
- Printer-friendly version
- Log in to post comments
- 3710 views