Warteschlangen (engl. queues) sind Datenstrukturen die auf dem FIFO Prinzip basieren:
| FIFO: First In, First Out |
Die Objekte die zuerst eingefügt werden, werden auch als erstes wieder ausgelesen. Warteschlangen erhalten die Reihenfolge der Ankunft indem Sie immer nur Objekte am Kopf entnehmen und immer nur Objekte am Ende der Warteschlange einfügen. Typische Operationen auf einer Warteschlange sind:
| Operation | Erklärung | Aufwand |
|---|---|---|
| peek | Lesen der Datenstruktur am Kopf der Warteschlange ohne sie zu entfernen | O(1) |
| read | Lesen der vordersten Datenstruktur am Kopf und gleichzeitiges Entfernen | O(1) |
| write | Einfügen einer neuen Datenstruktur am Ende der Warteschlange | O(1) |
| search | Suche nach einer Datenstruktur in der Warteschlange und Rückgabe der Position | O(n) |
| empty | Testen ob die Warteschlange leer ist | O(1) |
Wichtig: Warteschlangen bieten keinen wahlfreien Zugriff auf alle ihre Elemente
Warteschlangen sind im realen Leben häufig anzutreffen wenn es sich um Prozesse handelt die alle Beteiligten demokratisch, transparent (fair?) behandeln soll:
- Fließband
- Rolltreppe
- Warten bei vielen Dienstleistern wird als FIFO organisiert
In der Informatik sind Warteschlangen immer dann anzutreffen wenn die Erhaltung einer Ankunftsreihenfolge eine Rolle spielt:
- Datenbanksperren
- Eingehende Webserveranforderungen
- Transaktionales Arbeiten (Sitzplatzreservierung)
Implementierung
Warteschlange sind Spezialfälle von Listen. Im Unterschied zu einer Liste erlauben sie nur das Einfügen von Objekten am Ende und das Entfernen am Kopf der Warteschlange:
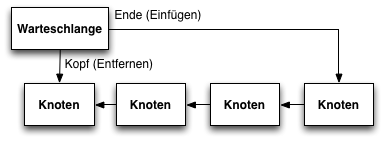
Ringpuffer
Warteschlangen die auf einfach oder zweifach verketteten Knoten beruhen sind sehr flexibel. Sie sind jedoch auch ineffizient da bei jedem Aufruf neue Knotenobjekte mit dem aufwendigen new() Operator erzeugt werden müssen.
Dies kann durch die Verwendung von ausreichend großen Ringpuffern vermieden werden, da hier die Knotenobjekte nur einmalig angelegt werden müssen. Diese Ringpuffer werden durch ein Feld R mit einer festen Größe n implementiert. Beim Erreichen des Endes des Feldes wird dieses durch ein Fortsetzen am Beginn des Feldes zum Ring "zusammengebogen".
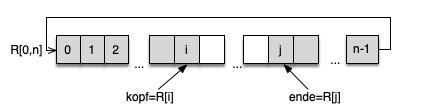
Hierzu benötigt man:
- einen Zeiger auf das Ende der Warteschlange (im Beispiel R[j])
- einen Zeiger auf den Kopf der Warteschlange (Im Beispiel R[i])
Beim Einfügen und Entfernen von Elementen werden beim Verrücken der Zeiger der Restwert nach der Division durch die Größe des Felds verwendet um nicht einen Feldüberlauf zu Erzeugen. Beim Einfügen eines neuen Elements in den Ringpuffer wird das neue Ende in Java wie folgt berechnet:
ende = (ende-1)%n;
Der Kopf wird nach dem Entfernen eines Elements wie folgt berechnet:
kopf = (kopf-1)%n;
Wichtig: Ringpuffer haben eine feste Größe. Es muss explizit eine Ausnahmebehandlung implementiert werden, wenn die Warteschlange über die Größe n des Feldes wächst.
- Printer-friendly version
- Log in to post comments
- 9199 views
Implementierung
Unter "Implementierung" steht, dass Warteschlangen nur das Einfügen und Entfernen von Objekten am Ende der Warteschlange erlauben.
Nach dem FIFO-Prinzip müsste aber das Entfernen am Kopf der Warteschlange geschehen und nicht am Ende, damit auch das zuerst eingefügte Element als erstes wieder entfernt wird.
Stimmt, irgendwie schon
Danke für den Hinweis. Ich habe das Skript angepasst. Kopf und Ende wurde hier etwas lax verwendet. Ich habe das Diagramm angepasst und nur noch eine Verzeigerung in eine Richtung eingemalt. Hierdurch sollte es keine Zweifel mehr geben.
Ringpuffer Grafik
Ist es richtig so, dass der kopf=r[j] und das ende auch =r[j] ist?
Sind beim Ringpuffer Anfang und Ende identisch, wenn das Feld sein Ende erreicht hat?
Dachte, dass das nicht so wäre, weshalb mich die Grafik da gerade etwas verwirrt.
Vielen Dank!
Toll beobachtet. Habe den Fehler im Diagramm korrigiert. Vielen Dank.