Die binäre Suche erfolgt nach dem "Teile und Herrsche" Prinzip (divide et impera) durch Teilen der zu durchsuchenden Liste.

Voraussetzung: Die Folge muss steigend oder fallend sortiert sein!

Der Algorithmus lässt sich sehr gut rekursiv beschreiben:

Suche in einer sortierten Liste L nach einem Schlüssel k:

• Beende die Suche erfolglos wenn die Liste leer ist
• Nimm das Element auf der mittleren Position m der Liste und Vergleiche es mit dem Schlüssel
  • Falls der Schlüssel k kleiner als dasElement L[m] is (k<L[m]) durchsuche die linke Teilliste bis zum Element L[m]
  • Falls der Schlüssel k größer als dasElement L[m] is (k>L[m]) durchsuche die rechte Teilliste vom Element L[m] bis zum Ende
  • Beende die Suche wenn der Schlüssel k gleich L[m] ist (k=L[m])

Das binäre Suchen ist ein Standardverfahren der Informatik da es sehr effizient ist. Der Aufwand beträgt selbst im ungünstigsten Fall O(N)=log₂(N).

Im günstigsten Fall ist der Aufwand O(N)=1 da eventuell der gesuchte Schlüssel sofort gefunden wird.

Beispiel einer binären Suche

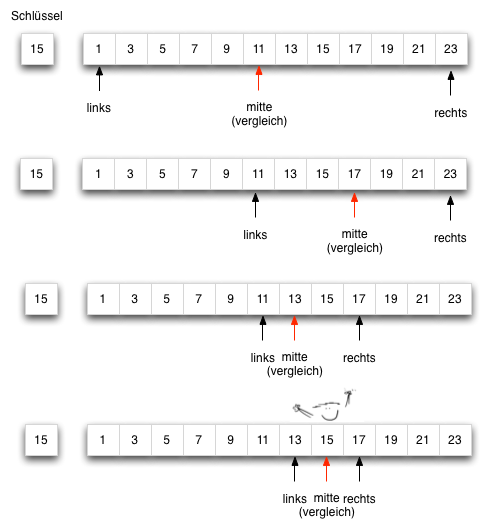
Das folgende Feld hat 12 Elemente zwischen 1 und 23. Es wird ein Element mit dem Wert 15 gesucht. Zu Beginn ist das Suchintervall das gesamte Feld von Position 0 (links) bis 11 (rechts). Der Vergleichswert (mitte) wird aus dem arithmetischen Mittel der Intervallgrenzen berechnet.

Beispielimplementierung in Java

Die Methode binaerSuche() sucht einen Kandidaten in einem aufsteigend sortierten Feld von Ganzzahlen. Das Hauptprogramm erzeugt ein Feld mit der Größe 200 und aufsteigenden Werten

public class Binaersuche {
    int[] feld;
   /**
     *
     * @param feld: Das zu durchsuchende Feld
     * @param links: linker Index des Intervalls
     * @param rechts: rechter Index des Intervalls
     * @param kandidat: der zu suchende Wert
     */
static void binaerSuche(int[] feld, int links,int rechts, int kandidat) {
        int mitte;
    do{
        System.out.println("Intervall [" + links +
                "," + rechts + "]");

            mitte = (rechts + links) / 2;
            if(feld[mitte] < kandidat){
                links = mitte + 1;
            } else {
                rechts = mitte - 1;
            }
     } while(feld[mitte] != kandidat && links <= rechts);
     if(feld[mitte]== kandidat){
            System.out.println("Position: " + mitte);
        } else {
            System.out.println("Wert nicht vorhanden!");
        }
    }

    public static void main(String[] args) {
        int groesse=200;
        int[] feld = new int[groesse];
        for (int i=0; i<feld.length;i++)
            feld[i] = 2*i; //Feld besteht aus geraden Zahlen
        System.out.println("Suche feld["+ 66 + "]=" + feld[66]);
        binaerSuche(feld, 0,(feld.length-1), feld[66]);
    }
}

Programmausgabe auf Konsole:

Suche feld[66]=132
Intervall [0,199]
Intervall [0,98]
Intervall [50,98]
Intervall [50,73]
Intervall [62,73]
Intervall [62,66]
Intervall [65,66]
Intervall [66,66]
Position: 66

Tipp: Nutzen Sie Arrays.binarySearch()

Die Systemklasse Arrays bietet nützliche Methoden zum Arbeiten mit Feldern an. Nutzen Sie die überladene, statische Methode Arrays.binarySearch() zum Suchen in einem Feld.
Das funktioniert natürlich nur in einem sortierten Feld. Dafür gibt es ja die überladene, statische Methode Arrays.sort()...

Ein Beispiel mit der main() Methode von oben:

    public static void main(String[] args) {
        int groesse=200;
        int[] feld = new int[groesse];
        for (int i=0; i<feld.length;i++)
            feld[i] = 2*i; //Feld besteht aus geraden Zahlen
        System.out.println("Suche feld["+ 66 + "]=" + feld[66]);
        Arrays.sort(feld);
        int ergebnis = Arrays.binarySearch(feld,feld[66]);
    }

Weiterführende Quellen und Beispiele

• Binäre Suche für Lego Fans