Suchalgorithmen
Suchalgorithmen |
Such- und Sortiervorgänge sind sehr häufige Aufgaben die in Anwendungen gelöst werden müssen. Suchen ist ein Vorgang der komplementär zum Sortieren ist. Datenbestände die vollständig oder teilweise sortiert sind, lassen sich wesentlich einfacher durchsuchen. Ungeordnete Datenbestände lassen sich lassen sich im schlechtesten Fall nur linear durchsuchen. Suchvorgänge lassen wie folgt kategorisieren:
|
Internes und externes Suchen
Man unterscheidet zwischen Suchvorgängen bei denen man den gesamten Datenbestand im Hauptspeicher verwalten kann (internes Suchen) und Suchvorgängen bei denen der Datenbestand nur teilweise in den Hauptspeicher geladen werden kann(externes Suchen).
Beim externen Suchen muss man also einen schnellen, aber begrenzten Hauptspeicher geschickt einsetzen um einen langsamen, aber kostengünstigeren Massenspeicher zu durchsuchen.
Die Unterscheidung zwischen den beiden Suchverfahren ist sehr wichtig für produktiv eingesetzte Anwendungen, in der Berechung der Zeitaufwände ist sie nicht hilfreich!
Ein Festplattenspeicher mag etwa 1000 mal langsamer als der Hauptspeicher eines Rechners sein. Dies macht bei einer echten Anwendung einen großen Unterschied. Bei der Berechnung der Zeitkomplexität wird dieser Faktor jedoch als "unbedeutend" weggekürzt.
Suchverfahren
- 7632 views
Sequentielle Suche (lineare Suche)
Sequentielle Suche (lineare Suche)Die sequentielle Suche beruht auf dem naiven Ansatz einen Datenbestand vollständig zu durchsuchen bis das passende Element gefunden wird. Dieses Verfahren nennt man auch erschöpfende Suche oder im englischen das Greedy-Schema (engl. für gefräßig). Der Algorithmus für das Durchsuchen eines Felds ist der folgende:
- Spezifiziere Suchschlüssel
- Vergleiche jedes Element mit dem Suchschlüssel
- Erfolgsfall: Liefere Indexposition beim ersten Auffinden des Objekts und beende das Suchen
- Kein Erfolg: Gehe zum nächsten Objekt und vergleiche es.
- Gib eine Meldung über das erfolglose Suchen zurück wenn das Ende des Datenbestands erreicht wurde, ohne daß, das Objekt gefunden wird. Dies kann eine java-Ausnahme sein oder ein spezieller Rückgabewert (z.Bsp .1)
Der Aufwand für diesen Algorithmus ist linear, also O(n). Die Anzahl der nötigen Vergleichsoperationen hängt direkt von der Anzahl der Elemente im Datenbestand ab. Im statischen Mittel sind dies n/2 Vergleiche.
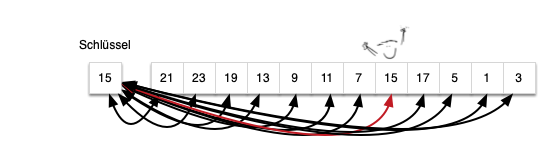
Sequentielle Suche in einem unsortierten Datenbestand
In diesem Fall muss bei jeder Suche der gesamte Datenbestand durchlaufen werden bis ein Element gefunden wurde
Beispiel einer Javaimplementierung
Die Methode sequentielleSuche() durchsucht ein Feld von 32 Bit Ganzzahlen nach einem vorgegebenen Schlüssel schluessel und gibt den Wert -1 zurück wenn kein Ergebnis gefunden wird.
public static int sequentielleSuche() (int[] feld, int schluessel) {
int suchIndex = 0;
while (suchIndex< feld.length && feld[suchIndex] != schluessel) suchIndex++;
if (suchIndex == feld.length) suchindex = -1; // Nichts gefunden
return suchindex;
}
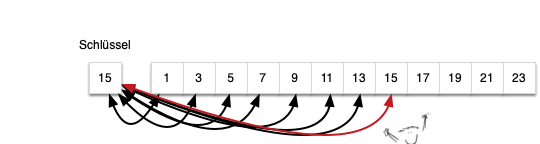
Sequentielle Suche in einem sortierten Datenbestand
Bei einem sortierten Datenbestand kann man die Suche optimieren in dem man sie abbricht so bald man weiß, das die folgenden Elemente alle größer bzw. kleiner als das gesucht Element sind. Man muss also nicht das Feld vollständig durchlaufen. Hierdurch lässt sich Zeit sparen. Der durchschnittliche Aufwand von n/2 bleibt jedoch ein linearer Aufwand.
Beispiel einer Javaimplementierung
Die Methode sequentielleSuche() durchsucht ein Feld von 32 Bit Ganzzahlen nach einem vorgegebenen Schlüssel schluessel und gibt den Wert -1 zurück wenn kein Ergebnis gefunden wird.
public static int sequentielleSuche() (int[] feld, int schluessel)
int suchIndex = 0;
while (suchIndex< feld.length && feld[suchIndex] < schluessel) suchIndex++;
if ((suchindex < feld.length) && (feld[suchIndex] == feld[schluessel]))
return suchindex; // Erfolg
else return -1; //kein Erfolg
}- 25830 views
Binäre Suche
Binäre SucheDie binäre Suche erfolgt nach dem "Teile und Herrsche" Prinzip (divide et impera) durch Teilen der zu durchsuchenden Liste.
Voraussetzung: Die Folge muss steigend oder fallend sortiert sein!
Der Algorithmus lässt sich sehr gut rekursiv beschreiben:
Suche in einer sortierten Liste L nach einem Schlüssel k:
- Beende die Suche erfolglos wenn die Liste leer ist
- Nimm das Element auf der mittleren Position m der Liste und Vergleiche es mit dem Schlüssel
- Falls der Schlüssel k kleiner als dasElement L[m] is (k<L[m]) durchsuche die linke Teilliste bis zum Element L[m]
- Falls der Schlüssel k größer als dasElement L[m] is (k>L[m]) durchsuche die rechte Teilliste vom Element L[m] bis zum Ende
- Beende die Suche wenn der Schlüssel k gleich L[m] ist (k=L[m])
Das binäre Suchen ist ein Standardverfahren der Informatik da es sehr effizient ist. Der Aufwand beträgt selbst im ungünstigsten Fall O(N)=log2(N).
Im günstigsten Fall ist der Aufwand O(N)=1 da eventuell der gesuchte Schlüssel sofort gefunden wird.
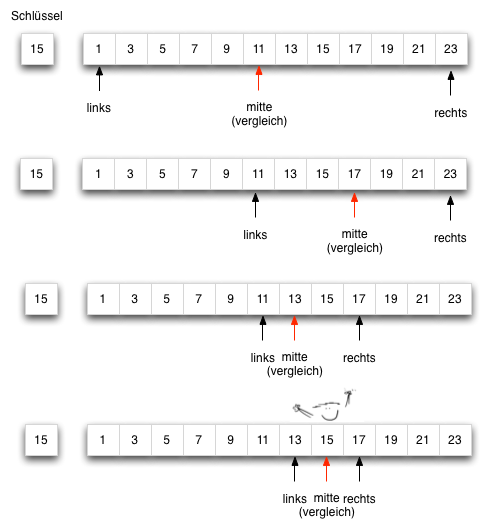
Beispiel einer binären Suche
Das folgende Feld hat 12 Elemente zwischen 1 und 23. Es wird ein Element mit dem Wert 15 gesucht. Zu Beginn ist das Suchintervall das gesamte Feld von Position 0 (links) bis 11 (rechts). Der Vergleichswert (mitte) wird aus dem arithmetischen Mittel der Intervallgrenzen berechnet.
Beispielimplementierung in Java
Die Methode binaerSuche() sucht einen Kandidaten in einem aufsteigend sortierten Feld von Ganzzahlen. Das Hauptprogramm erzeugt ein Feld mit der Größe 200 und aufsteigenden Werten
public class Binaersuche {
int[] feld;
/**
*
* @param feld: Das zu durchsuchende Feld
* @param links: linker Index des Intervalls
* @param rechts: rechter Index des Intervalls
* @param kandidat: der zu suchende Wert
*/static void binaerSuche(int[] feld, int links,int rechts, int kandidat) {
int mitte;
do{
System.out.println("Intervall [" + links +
"," + rechts + "]");
mitte = (rechts + links) / 2;
if(feld[mitte] < kandidat){
links = mitte + 1;
} else {
rechts = mitte - 1;
}
} while(feld[mitte] != kandidat && links <= rechts);
if(feld[mitte]== kandidat){
System.out.println("Position: " + mitte);
} else {
System.out.println("Wert nicht vorhanden!");
}
}
public static void main(String[] args) {
int groesse=200;
int[] feld = new int[groesse];
for (int i=0; i<feld.length;i++)
feld[i] = 2*i; //Feld besteht aus geraden Zahlen
System.out.println("Suche feld["+ 66 + "]=" + feld[66]);
binaerSuche(feld, 0,(feld.length-1), feld[66]);
}
}
Programmausgabe auf Konsole:
Suche feld[66]=132
Intervall [0,199]
Intervall [0,98]
Intervall [50,98]
Intervall [50,73]
Intervall [62,73]
Intervall [62,66]
Intervall [65,66]
Intervall [66,66]
Position: 66
Tipp: Nutzen Sie Arrays.binarySearch()
Die Systemklasse Arrays bietet nützliche Methoden zum Arbeiten mit Feldern an. Nutzen Sie die überladene, statische Methode Arrays.binarySearch() zum Suchen in einem Feld.
Das funktioniert natürlich nur in einem sortierten Feld. Dafür gibt es ja die überladene, statische Methode Arrays.sort()...
Ein Beispiel mit der main() Methode von oben:
public static void main(String[] args) {
int groesse=200;
int[] feld = new int[groesse];
for (int i=0; i<feld.length;i++)
feld[i] = 2*i; //Feld besteht aus geraden Zahlen
System.out.println("Suche feld["+ 66 + "]=" + feld[66]);
Arrays.sort(feld);
int ergebnis = Arrays.binarySearch(feld,feld[66]);
}
Weiterführende Quellen und Beispiele
- 39430 views
Wieso Feldgröße / 3
Wieso teile ich meine groesse = 200 durch 3 und nicht durch 2? der suchalgorithmus fängt doch in der Mitte an oder ist mit der ersten Ausgabe etwas anderes gemeint?
- Log in to post comments
Beispielanwendung zum Suchen
Beispielanwendung zum SuchenDas folgende Programm zeigt eine sequentielle und eine binäre Suche in einem Feld mit zufälligen Werten.
Die Variable groesse erlaubt es die Größe des Felds zu verändern. Mit dem Nanotimer werden die benötigten Zeiten gemessen. Vergleichen Sie die Zeitaufwände für das sequentielle und das binäre Suchen mit dem Zeitaufwand für das Sortieren mit der Hilfklasse Arrays!
package s2.sort;
import java.util.Arrays;
/**
*
* @author sschneid
* @version 1.0
*/
public class Suchen {
public static int[] feld;
public static int groesse = 10000000;
/**
* Hauptprogramm
* @param args
*/
public static void main(String[] args) {
erzeugeFeld();
int suchwert =feld[groesse-2];
System.out.println("Suche feld["+ (groesse-2) +"] = " + suchwert);
sucheSequentiell(suchwert);
sortiere();
binaereSucheSelbst(suchwert);
binaereSuche(suchwert);}
/**
* Erzeuge ein Feld mit Zufallszahlen
*/
public static void erzeugeFeld() {
feld = new int[groesse];
for (int i=0; i<feld.length;i++) {
feld[i]=(int)(Math.random() * (double)Integer.MAX_VALUE);
}
System.out.println("Feld mit "+ groesse + " Elementen erzeugt.");
}
/**
* Suche sequentiell einen Wert in einem unsortierten Feld
* @param suchwert der gesuchte Wert
*/
public static void sucheSequentiell(int suchwert) {
System.out.println("Sequentielle Suche nach Schlüssel");
long t = System.nanoTime();
int i=0;
while ( (i<groesse) && (suchwert != feld[i])) i++;
t = (System.nanoTime() -t)/1000000;
if (i== groesse) {
System.out.println(" Der Wert: " + suchwert +
" wurde nicht gefunden");
}
else {
System.out.println(" Der Suchwert wurde auf Position " + i +
" gefunden");
}
System.out.println(" Dauer sequentielle Suche: " + t +"ms");
}
/**
* Sortiere ein Feld mit der Klasse Arrays und messe die Zeit
* @param suchwert der gesuchte Wert
*/
public static void sortiere() {
System.out.println("Sortieren mit Arrays.sort()");
long t = System.nanoTime();
Arrays.sort(feld);
t = (System.nanoTime() -t)/1000000;
System.out.println(" Feld sortiert in " + t +" ms");
}
/**
* Suche binär einen Wert in einem sortierten Feld
* @param suchwert der gesuchte Wert
*/
public static void binaereSucheSelbst(int suchwert) {
System.out.println("Selbstimplementierte binäre Suche");
long t = System.nanoTime();
int intervall = (feld.length+1)/2;
int pos = intervall;
while ((intervall > 1) && (feld[pos] != suchwert)) {
intervall =(intervall+1)/2;
if ((feld[pos] > suchwert)) {pos -= intervall;}
else {pos += intervall;}
}
t = (System.nanoTime() -t);
if (feld[pos]== suchwert) {
System.out.println(" Der Suchwert wurde auf Position " +
pos +" gefunden");
}
else {
System.out.println(" Der Wert: " + suchwert +
" wurde nicht gefunden");
}
System.out.println(" Dauer binäre Suche " + (t/1000000) +"ms" +
" (" + t + " ns)");
}
/**
* Suche binär einen Wert in einem sortierten Feld
* Nutze die binäre Suchmethode der Klasse Arrays
* @param suchwert der gesuchte Wert
*/
public static void binaereSuche(int suchwert) {
System.out.println("Binäre Suche mit Arrays.binarySearch()");
long t = System.nanoTime();
int pos = Arrays.binarySearch(feld, suchwert);
t = (System.nanoTime() -t);
System.out.println(" Der Suchwert wurde auf Position " +
pos +" gefunden");
System.out.println(" Dauer binäre Suche " + (t/1000000) +
"ms" + " (" + t + " ns)");
}}
Klasse in github.
Typische Konsolenausgabe:
Feld mit 10000000 Elementen erzeugt.
Suche feld[9999998] = 1719676120
Sequentielle Suche nach Schlüssel
Der Suchwert wurde auf Position 9999998 gefunden
Dauer sequentielle Suche: 28ms
Sortieren mit Arrays.sort()
Feld sortiert in 1296 ms
Selbstimplementierte binäre Suche
Der Suchwert wurde auf Position 8008593 gefunden
Dauer binäre Suche 0ms (6000 ns)
Binäre Suche mit Arrays.binarySearch()
Der Suchwert wurde auf Position 8008593 gefunden
Dauer binäre Suche 0ms (11000 ns)
- 8121 views