Datenstrukturen
DatenstrukturenEinführung
Das Zusammenfassen von Objekten, Datenstrukturen zu einer Menge von Objekten ist eine typische Anforderung in der Informatik. Zur Lösung dieses Anforderung müssen die folgenden Aspekte betrachtet werden:
- Ist die Menge der Objekte statisch oder kann sie sich veränderen. Ist sie dynamisch?
- Bilden die Elemente der Menge eine bestimmte Reihenfolge?
- Ist die Position des Elements in der Menge wichtig? Muss das Objekt über seine Position zugreifbar sein?
- Sollen Elemente zur Laufzeit zur Menge hinzugefügt oder entfernt werden können?
- Reicht es zu wissen, dass ein Element zur Menge gehört?
- Muss der Zugriff der Elemente über eine Nachbarschaftsbeziehung gegeben sein?
- Müssen die Elemente einer bestimmten Sortierreihenfolge genügen (z. Bsp. lexikographische Ordnung?)
- Ist es erlaubt Duplikate in der Menge zu verwalten?
Beispiele aus dem echten Leben
Welche der oben geforderten Kriterien gelten hier?
- Bierkasten mit Bierflaschen (Antialkoholiker mögen mit einem Kasten Sprudel arbeiten)
- Schulheft mit Seiten
- Ringbuch mit Seiten
- Ringbuch mit Seiten und Trennern
Felder
Die bisher verwendete Datenstruktur zum Verwalten von Objekten war das Feld (Array). Ein Feld hat die folgenden Vorteile:
- Sehr schneller, indexierter Zugriff auf ein Objekt über dessen Position im Feld: O(1)
- Konstante Größe
Diesen Vorteilen stehen die folgenden Nachteile gegenüber:
- Aufwändiges Einfügen: O(n)
- Feld muss bei einer nötigen Vergrößerung umkopiert werden.
Die Referenz ist die zweite Datenstruktur mit der Objekte verwaltet werden können. Sie erlaubt jedoch nur den direkten Zugriff auf ein einzelnes Objekt.
Dynamische Datenstrukturen
Zur Verwaltung von beliebig vielen Objekten verwendet man dynamische Datenstrukturen in Java die man durch Verkettung von Objekten mit Objektreferenzen erhält.
Die Datenstrukturen sind dynamisch, da während der Laufzeit beliebig viele Objekte in sie eingefügt oder aus ihnen entfernt werden können. Die Anzahl ihrer Objekte (Knoten) ist nicht vorab festgelegt.
| Knoten |
|---|
| Ein Knoten ist ein Bestandteil einer verkettenden, dynamischen Datenstruktur. In Java werden Knoten durch Objekte und Referenzen, die auf die Knoten zeigen, realisiert |
Verketteten Datenstrukturen können linear (nicht verzweigt) oder auch verzweigt sein.
- Lineare Datenstrukturen sind typischerweise Listen, Warteschlangen, Stacks
- Verzweigte Datenstrukturen finded man typischerweise in Bäumen
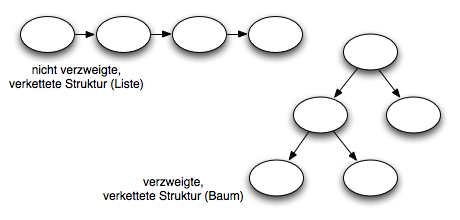
Vertreter dynamischer Datenstrukturen
- 8093 views
Listen
ListenListen sind verkettete Datenstrukturen, die im Gegensatz zu Feldern dynamisch wachsen können um beliebig viele Elemente (Knoten) zu verwalten. Sie werden anstatt Felder verwendet wenn
- die maximale Größe nicht vorab bekannt ist
- kein wahlfreier Zugriff auf beliebige Listenelemente (bzw. Knoten) benötigt wird.
- die Reihenfolge der Knoten wichtig ist.
Typische Operationen die für Listen zur Verfügung stehen sind:
| Operation | Beschreibung | Aufwand |
|---|---|---|
| Einfügen | Einfügen von Knoten in die Liste | O(n) |
| Entfernen | Entfernen von Knoten aus der Liste | O(n) |
| Tauschen | Veränderung der Knotenreihenfolge | O(n) |
| Länge bestimmen | Bestimmung der Länge der Liste (bei Pflege der Länge) | O(1) |
| Existenz | Abfrage ob ein Knoten in der Liste enthalten ist | O(n) |
| Einfügen am Kopf/Ende | Bei Pflege von Zeigern auf Anfang und Ende der Liste! | O(1) |
Mit Hilfe von Listen können auch spezialisiertere Datenstrukturen wie Warteschlangen (engl. queues) oder Stapel (engl. stack) implementiert werden.
Listen in Java
Eine verkettete Datenstruktur kann mit jeder Javaklasse aufgebaut werden die in der Lage ist auf Objekte der gleichen Klasse zu zeigen.
Eine solche Verkettung kann man zum Beispiel mit jeder Klasse implementieren, die die folgende Schnittstelle implementiert:
package s2.listen;
/**
*
* @author s@scalingbits.com
*/
public interface EinfacherListenknoten {
/**
* Einfuegen eines Nachfolgers
* @param n einzufuegender Listenknoten
*/
public void setNachFolger(EinfacherListenknoten n);
/**
* Auslesen des Nachfolgers
* @return der Nachfolger
*/
public EinfacherListenknoten getNachfolger();
}
Dies geschieht im folge für die Klasse Ganzzahl, die neben der Listeneigenschaft auch in der Lage ist eine Ganzzahl zu verwalten:
package s2.listen;
/**
*
* @author s@scalingbits.com
*/
public class Ganzzahl implements EinfacherListenknoten {
public int wert;
private EinfacherListenknoten naechsterKnoten;
public Ganzzahl(int i) {
wert = i;
naechsterKnoten = null;
}
/**
* Einfuegen eines Nachfolgers
* @param n einzufuegender Listenknoten
*/
@Override
public void setNachFolger(EinfacherListenknoten n) {
naechsterKnoten = n;
}
/**
* Auslesen des Nachfolgers
* @return der Nachfolger
*/
@Override
public EinfacherListenknoten getNachfolger() {
return naechsterKnoten;
}
/**
* Hauptprogramm zum Testen
* @param args
*/
public static void main(String[] args) {
Ganzzahl z1 = new Ganzzahl(11);
Ganzzahl z2 = new Ganzzahl(22);
Ganzzahl z3 = new Ganzzahl(33);
z1.setNachFolger(z2);
z2.setNachFolger(z3);
}
}In UML:
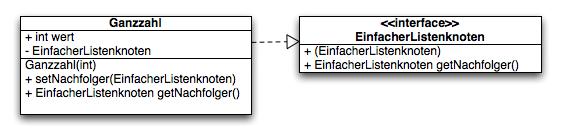
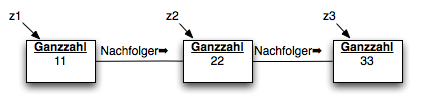
Zum Zugriff auf diese Liste reicht jetzt die Referenzvariable z1. Alle anderen Knoten können mit Hilfe der Methode getNachfolger() erreicht werden. Es existiert jedoch kein wahlfreier Zugriff auf die Knoten der Liste.
Werden die beiden Variablen z2 und z3 dereferenziert, können die einzelnen Knoten nach wie vor erreicht werden:
z2 = null; z3 = null;
Wird die Variable z1 dereferenziert,
z1 = null;
sind alle drei Objekte nicht mehr erreichbar und können vom Garbagekollektor gelöscht werden.
Unsortierte Listen
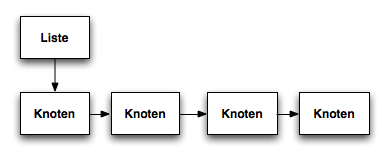
Im einfachsten Fall kann eine Liste als einfach verzeigerte Liste implementiert die nur auf den Kopfknoten zeigt.
- Das Einfügen und Löschen am Kopfende hat einen konstanten Aufwand
- Das Suchen bzw. Löschen von Knoten hat einen Aufwand von O(n)
- Relativer Zugriff von einem bekannten Knoten ist nur in Richtung der Nachfolger möglich.
Bei Listen kann man auch das Ende der Liste im Listenobjekt mit pflegen. Einfüge- und Entnahmeoperationen werden hierdurch aufwendiger zu implementieren. Der Vorteil liegt jedoch darin, dass auf das Ende der Liste wahlfrei zugegriffen werden kann.
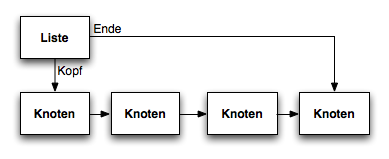
Vorteile einfach verzeigerter Listen mit Referenz auf das Ende der Liste
- Zugriff auf das und erste und letzte Element der Liste mit konstantem Aufwand
- Iterieren über die Menge aller Listenelemente ist möglich
- Löschen des letzten Elements ist mit konstantem Aufwand möglich (Hierdurch kann eine Warteschlange implementiert werden)
Nachteile
- Kein wahlfreier Zugriff auf alle Elemente
- Man kann nur auf ein Nachbarelement (den Nachfolger) mit konstantem Aufwand zugreifen
Zweiseitig verzeigerte Listen haben den Vorteil, dass sie einen direkten Zugriff auf den Vorgängerknoten sowie auf den Nachfolgerknoten haben:
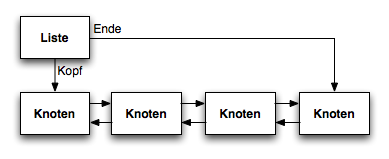
Vorteile (über die einfach verzeigerte Liste hinaus):
- Iterieren ist in zwei Richtungen möglich
- Der Vorgängerknoten eines Listenknoten kann auch mit konstantem Aufwand errreicht werden
- 6857 views
Übungen (Listen)
Übungen (Listen)Doppelt verzeigerte Liste mit Referenz auf das Ende der Liste
Implementieren Sie eine doppelt verzeigerte Liste zur Verwaltung ganzer Zahlen. Der Listenkopf referenziert auf das Kopfelement sowie auf das letzte Element der Liste
Eine Liste mit drei Knoten soll wie folgt implementiert sein:
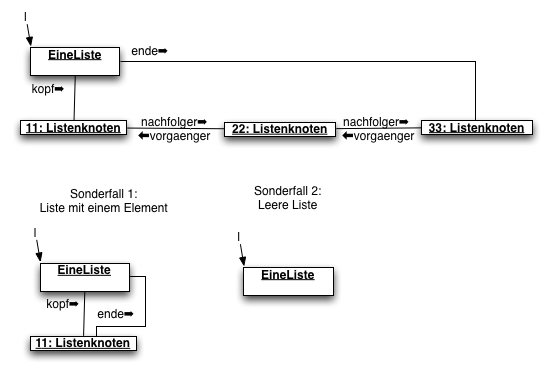
Beachten Sie die die beiden Sonderfälle einer Liste mit einem Element und den Sonderfall einer leeren Liste.
Zur beschleunigten Implementierung sind alle Klassen schon gegeben
- ListenKnoten: Eine einfache Klasse zur Verwaltung ganzer Zahlen mit Referenzen auf Vorgänger- und Nachfolgerknoten
- MainTestListe: Ein Hauptprogramm mit diversen Testroutinen zum Testen der Liste
- EineListe: Eine Rahmenklasse die vervollständigt werden soll. Implementieren Sie die folgenden Methoden:
- einfuegeAnKopf(einfuegeKnoten): Einfügen eines Knotens am Kopf der Liste
- laenge(): Berechnung der Länger der Liste
- loesche(Knoten): Löschen eines Knotens einer Liste
- enthaelt(Knoten): Prüfung ob ein Knoten in der Liste enthalten ist. Die Prüfung erfolgt auf Objektidentität, nicht auf Wertgleichheit
- einfuegeNach(nachKnoten,einfuegeKnoten): Einfügen eines neuen Knotens einfuegeKnoten hinter dem Knoten nachKnoten
 |
Warum werden die Methoden in EineListe und nicht in ListenKnoten implementiert?
|
UML Diagramm der drei Klassen:
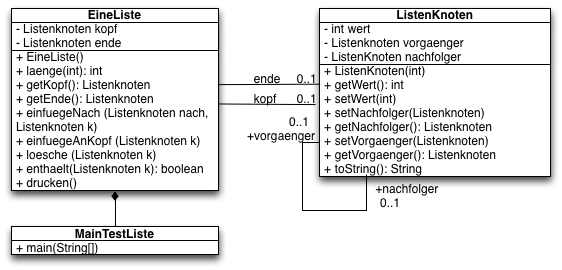
Klasse Listenknoten
package s2.listen;
/**
*
* @author s@scalingbits.com
*/
public class Listenknoten {
private Listenknoten vorgaenger;
private Listenknoten nachfolger;
private int wert;
public Listenknoten(int einWert) { wert=einWert;}
public Listenknoten getNachfolger() { return nachfolger;}
public void setNachfolger(Listenknoten nachfolger) {
this.nachfolger = nachfolger;
}
public Listenknoten getVorgaenger() {
return vorgaenger;
}
public void setVorgaenger(Listenknoten vorgaenger) {
this.vorgaenger = vorgaenger;
}
public int getWert() {
return wert;
}
public void setWert(int wert) {
this.wert = wert;
}
/**
* Erlaubt den Zahlenwert als Text auszudrucken
* @return
*/
@Override
public String toString() { return Integer.toString(wert);}
}Klasse EineListe
Vervollständigen Sie die folgende Klasse
package s2.listen;
/**
*
* @author s@scalingbits.com
*/
public class EineListe {
protected Listenknoten kopf;
protected Listenknoten ende;
/**
* Konstrukor. Erzeuge eine leere Liste
*/
public EineListe() {
kopf = null;
ende = null;
}
/**
* Berechne die Länge der Liste
* @return Länge der Liste
*/
public int laenge() {
int laenge = 0;
System.out.println("1. Implementieren Sie EineListe.laenge()");
return laenge;
}
/**
* Liefert den Kopf der Liste oder einen Null Zeiger
* @return
*/
public Listenknoten getKopf() {
return kopf;
}
/**
* Liefert das Ende der Liste oder einen Null Zeiger
* @return
*/
public Listenknoten getEnde() {
return ende;
}
/**
* Drucke eine Liste alle Objekte auf der Konsole
*/
public void drucken() {
System.out.println("Länge Liste: " + laenge());
Listenknoten k = kopf;
while (k != null) {
System.out.println("Knoten: " + k);
k = k.getNachfolger();
}
}
/**
* Füge hinter dem Listenknoten "nach" den Knoten "k"ein.
* Füge nichts ein wenn der Listenknoten "nach" nicht in der Liste
* vorhanden ist
* @param nach
* @param k
*/
public void einfuegeNach(Listenknoten nach, Listenknoten k) {
System.out.println("5. Implementieren Sie EineListe.einfuegeNach()");
}
/**
* Füge einen Listenknoten am Kopf der Liste ein
* @param k neuer Listenknoten
*/
public void einfuegeAnKopf(Listenknoten k) {
System.out.println("2. Implementieren Sie EineListe.einfuegeAnKopf()");
}
/**
* Lösche einen Knoten aus der Liste. Mache nichts falls es nichts zu
* gibt
* @param k zu löschender Listenknoten
*/
public void loesche(Listenknoten k) {
System.out.println("3. Implementieren Sie EineListe.loesche()");
} // Ende Methode loesche()
/**
* Ist wahr wenn ein Knoten mit dem gleichen Wert existiert
* @param k
* @return
*/
public boolean enthaelt(Listenknoten k) {
boolean result = false;
System.out.println("4. Implementieren Sie EineListe.enthaelt()");
return result;
} // Ende Methode enhaelt()
} // Ende der Klasse EineListeKlasse MainTestListe
package s2.listen;
/**
*
* @author s@scalingbits.com
*/
public class MainTestListe {
/**
* Testroutinen für einfache Listen
* @param args
*/
public static void main(String[] args) {
EineListe testListe = new EineListe();
einfuegeTest(testListe, 4, 6);
System.out.println("Kontrolle: Drei Knoten von 4 bis 6");
einfuegeTest(testListe, 1, 3);
System.out.println("Kontrolle: Sechs Knoten von 1 bis 6");
einfuegeTest(testListe, 21, 27);
System.out.println("Kontrolle: 13 Knoten von 21 bis 27, 1 bis 6");
loeschenEndeTest(testListe, 3);
System.out.println("Kontrolle: 10 Knoten von 21 bis 27, 1 bis 3");
loeschenKopfTest(testListe, 8);
System.out.println("Kontrolle: 2 Knoten von 2 bis 3");
loeschenKopfTest(testListe, 3);
System.out.println("Kontrolle: 0 Knoten. Versuch löschen in leerer Liste");
enthaeltTest(testListe, 10);
System.out.println("Kontrolle: Einfügen in der Liste");
testListe = new EineListe();
einfuegeNachTest(testListe, 10);
}
/**
* Einfügen einer Reihe von Zahlen in eine gegebene Liste
* @param l Liste in die eingefügt wird
* @param min kleinster Startknoten der eingefügt wird
* @param max größter Knoten der eingefügt werden
*/
public static void einfuegeTest(EineListe l, int min, int max) {
System.out.println("Test: Einfügen am Kopf [" + min + " bis " + max + "]");
for (int i = max; i >= min; i--) {
l.einfuegeAnKopf(new Listenknoten(i));
System.out.println("Länge der Liste: " + l.laenge());
}
l.drucken();
}
/**
* Lösche eine bestimmte Anzahl von Knoten am Ende der Liste
* @param l Liste aus der Knoten gelöscht werden
* @param anzahl der zu loeschenden Knoten
*/
public static void loeschenEndeTest(EineListe l, int anzahl) {
System.out.println("Test: Löschen am Ende der Liste " + anzahl + "fach:");
for (int i = 0; i < anzahl; i++) {
l.loesche(l.ende);
System.out.println("Länge der Liste: " + l.laenge());
}
l.drucken();
}
public static void loeschenKopfTest(EineListe l, int anzahl) {
System.out.println("Test: Löschen am Kopf der Liste " + anzahl + "fach:");
for (int i = 0; i < anzahl; i++) {
l.loesche(l.getKopf());
System.out.println("Länge der Liste: " + l.laenge());
}
l.drucken();
}
public static void enthaeltTest(EineListe l, int groesse) {
System.out.println("Test: enhaelt() " + groesse + " Elemente");
Listenknoten[] feld = new Listenknoten[groesse];
for (int i = 0; i < groesse; i++) {
feld[i] = new Listenknoten(i * 10);
l.einfuegeAnKopf(feld[i]);
}
l.drucken();
for (int i = 0; i < groesse; i++) {
if (l.enthaelt(feld[0])) {
System.out.println("Element " + feld[i] + " gefunden");
}
}
System.out.println("Erfolg wenn alle Elemente gefunden wurden");
Listenknoten waise = new Listenknoten(4711);
if (l.enthaelt(waise)) {
System.out.println("Fehler: Element gefunden welches nicht zur Liste gehört!");
} else {
System.out.println("Erfolg: Element nicht gefunden welches nicht zur Liste gehört");
}
}
public static void einfuegeNachTest(EineListe l, int max) {
System.out.println("Test: einfügen nach " + max + "fach");
Listenknoten[] feld = new Listenknoten[max];
for (int i = 0; i < max; i++) {
feld[i] = new Listenknoten(i*10);
l.einfuegeAnKopf(feld[i]);
}
System.out.println("Länge der Liste: " + l.laenge());
for (int i = 0; i < max; i++) {
l.einfuegeNach(feld[i], new Listenknoten(feld[i].getWert()+1));
System.out.println("Länge der Liste: " + l.laenge());
}
l.einfuegeNach(l.ende, new Listenknoten(111));
l.drucken();
}
}
- 5555 views
Lösungen
LösungenDoppelt verzeigerte Liste mit Referenz auf das Ende der Liste
Klasse EineListe
Hinweis: Ändern Sie den Namen von EineListeLoseung an den zwei Stellen zu EineListe.
package s2.listen;/**
*
* @author s@scalingbits.com
*/
public class EineListeLoesung {
protected Listenknoten kopf;
protected Listenknoten ende;
public EineListeLoesung() {
kopf = null;
ende = null;
}
/**
* Berechnet die Anzahl der Listenelemente
* @return Anzahl der Listenelemente
*/
public int laenge() {
int laenge = 0;
Listenknoten zeiger = kopf;
while (zeiger != null) {
laenge++;
zeiger = zeiger.getNachfolger();
}
return laenge;
}
/**
* Liefert den Kopf der Liste oder einen Null Zeiger
* @return Zeiger auf Kopf der Liste
*/
public Listenknoten getKopf() {
return kopf;
}
/**
* Liefert das Ende der Liste oder einen Null Zeiger
* @return Zeiger auf das Ende der Lister
*/
public Listenknoten getEnde() {
return ende;
}
/**
* Drucke eine Liste alle Objekte auf der Konsole
*/
public void drucken() {
System.out.println("Länge Liste: " + laenge());
Listenknoten k = kopf;
while (k != null) {
System.out.println("Knoten: " + k);
k = k.getNachfolger();
}
}
/**
* Füge hinter dem Listenknoten "nach" den Knoten "k"ein.
* Füge nichts ein wenn der Listenknoten "nach" nicht in der Liste
* vorhanden ist
* @param nach
* @param k
*/
public void einfuegeNach(Listenknoten nach, Listenknoten k) {
Listenknoten t;
t = kopf; // Diese Variable wird über die Listenknoten laufen
while ((t != null) && (t != nach)) {
// Iteriere über die Liste solange Knoten existieren
// und kein passender gefunden hier
t = t.getNachfolger();
}
if (t == nach) { // Der Knoten wurde gefunden
// Merken des Nachfolger hinter der Einfuegestelle
Listenknoten derNaechste = nach.getNachfolger();
if (derNaechste != null) {
// Setzen des neuen Vorgängers falls es einen Nachfolger gab
derNaechste.setVorgaenger(k);
} else { // Wir haben am Ende eingefuegt. Ende-Zeiger korrigieren
ende = k;
}
// Der neu eingefügte Knoten soll auf den Nachfolger zeigen
k.setNachfolger(derNaechste);
// Der gesuchte Knoten ist der Vorgaenger. Der neue Knoten
// soll auf ihn zeigen
k.setVorgaenger(t);
// Der Vorgaenger soll auf den neu einfeügten Knoten zeigen
t.setNachfolger(k);
}
}
/**
* Füge einen Knoten am Anfang der Liste ein
* @param k
*/
public void einfuegeAnKopf(Listenknoten k) {
k.setVorgaenger(null);
if (kopf == null) { // Die Liste ist leer
ende = k; // Das Ende ist auch der Kopf
k.setNachfolger(null); // Sicherstellen das kein Nachfolger benutzt wird
} else { // Liste ist nicht leer
k.setNachfolger(kopf); // Neuer Nachfolger ist alter Kopf
kopf.setVorgaenger(k); // Alter Kopf bekommt Vorgaenger
}
kopf = k; // Es gibt einen neuen Kopf. Heureka
}
public void loesche(Listenknoten k) {
Listenknoten t = kopf; // Diese Variable wird über die Listenknoten laufen
if (kopf == null) {
System.out.println("Löschversuch auf leerer Liste");
} else {
//Pflege der Kopf- bzw Endezeiger
if (kopf == k) {
// Das Kopfelement wir geloescht
kopf = k.getNachfolger(); //Kann auch Null sein...
}
if (ende == k) {
// Das zu loeschende Objekt ist das Letzte
ende = k.getVorgaenger(); // Kann auch Null sein...
}
while ((t != null) && (t != k)) {
// Iteriere über Liste solange Nachfolger da sind
// und nichts passendes gefunden wird
t = t.getNachfolger();
}
if (t == k) { // Der Knoten wurde gefunden
Listenknoten nachf = k.getNachfolger();
Listenknoten vorg = k.getVorgaenger();
if (nachf != null) {
// Es gibt einen Nachfolger. Pflege dessen Vorgaenger
nachf.setVorgaenger(vorg);
}
if (vorg != null) {
// Es gibt einen Vorgaenger. Pflege dessen Nachfolger
vorg.setNachfolger(nachf);
}
// Entfernen aller Referenzen des geloeschten Objekts
t.setNachfolger(null);
t.setVorgaenger(null);
} // Ende der Knoten wurde gefunden
} // Ende Loeschen aus einer nicht leeren Liste
} // Ende Methode loesche
/**
* Ist wahr wenn ein Knoten mit dem gleichen Wert existiert
* @param k
* @return
*/
public boolean enthaelt(Listenknoten k) {
Listenknoten t = kopf;
boolean result = false;
while ((result == false) && (t != null)) {
result = (t == k);
if (!result) {
t = t.getNachfolger();
}
}
return result;
} // Ende Methode enhaelt()
} // Ende der Klasse EineListe
- 3709 views
Stapel (Stack)
Stapel (Stack)Der Stapel (engl. Stack) ist eine der wichtigsten Grundstrukturen der Informatik. Er funktioniert nach dem Prinzip, dass man bildlich gesprochen Elemente stapelt und immer nur auf das oberste Element des Stapels zugreifen kann um es zu lesen oder zu entfernen. Stapel werden daher im Englischen auch mit LIFO abgekürzt:
| LIFO: Last In First Out |
Hierdurch ergeben sich die typischen Operationen die für einen Stapel (in englisch) definiert sind:
| Operation | Erklärung | Aufwand |
|---|---|---|
| peek | Lesen der obersten Datenstruktur ohne sie zu entfernen | O(1) |
| pop | Lesen der obersten Datenstruktur und gleichzeitiges Entfernen | O(1) |
| push | Einfügen einer neuen Datenstruktur als oberste Datenstruktur | O(1) |
| search | Suche nach einer Datenstruktur im Stapel und Rückgabe der Position (naive Implementierung) | O(n) |
Java verfügt bereits über eine Implementierung von Stapeln in der Klasse java.util.Stack in der die oben genannten Operationen als Methoden für beliebige Instanzen der Klasse Object zur Verfügung stehen.
Stapel sind im realen Leben nicht ganz so häufig anzutreffen wie in der Informatik. Ein sehr gutes Beispiel aus dem realen Leben sind
- Teller die typischerweise aufeinander gestapelt werden. Der letzte Teller den man auf einen Stapel von Tellern legt ist auch typischerweise der erste Teller den man wieder von einem Stapel nimmt.
- Passagiere die eine Flugzeug besteigen und es dann in umgekehrter Reihenfolge verlassen. (Die strenge Implementierung eines Stapel/Stacks ohne Ausnahmen ist hier weder für die Fluggesellsschaft noch für die Passagiere akzeptabel)
- Eine Einzelgarage mit einem Fahrzeugabstellplatz vor der Garage. Dies ist ein Stapel/Stack der Tiefe zwei
- Ein Abstellgleis mit Prellbock.
In der Informatik sind Stapel sehr nützlich, wann immer man einen Zustand speichern muss um sich etwas Anderem zu widmen, und dann wieder auf den alten Zustand zurückzugreifen. Beispiele hierfür sind
- Verwalten von Variablen bei Methodenaufrufen in Java: Beim jedem Aufruf einer Methode werden die Variablen der aktuellen Methode auf von den Variablen der aufgerufenen Methode verdeckt(Push). Die Variablen der aufgerufenen Methode sind eine Datenstruktur die neu auf den Stapel gelegt wurden und die Variablen der alten Methode verdecken. Nach dem Abarbeiten der neuen Methode werden deren Variablen wieder gelöscht(Pop) und die Variablen der vorhergehenden Methode stehen wieder zur Verfügung
- Parsen (Analysieren) von Programiersprachen, Ausdrücken und Termen wie zum Beispiel ein mathematischer Term: 5 + 4*3. Hier wird bei der Analyse von 5 und "+" festgestellt, dass der zweite Operand (4*3) selbst wieder ein Term ist. Das Parsen der Addition wird angehalten. Die nötigen Datenstrukturen zum Parsen der Multiplikation werden angelegt und verdecken die Addition(Pop). Der Wert von 4*3 wird berechnet. Alle Datenstrukturen die zur Berechnung der Multiplikation benötigt wurden können jetzt wieder gelöscht werden (POP) um mit der ursprünglichen Multiplikation fortzufahren.
Beispiel: Die Auswertung des Terms 5+4*3
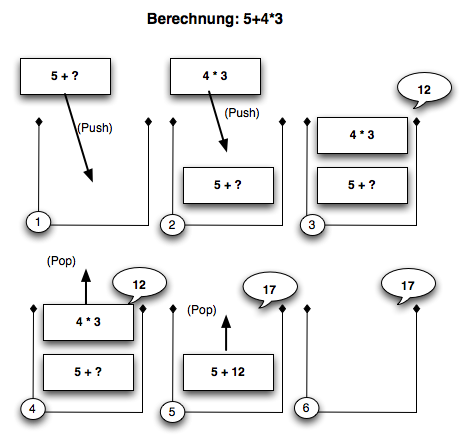
- 11525 views
Warteschlangen (Queues)
Warteschlangen (Queues)Warteschlangen (engl. queues) sind Datenstrukturen die auf dem FIFO Prinzip basieren:
| FIFO: First In, First Out |
Die Objekte die zuerst eingefügt werden, werden auch als erstes wieder ausgelesen. Warteschlangen erhalten die Reihenfolge der Ankunft indem Sie immer nur Objekte am Kopf entnehmen und immer nur Objekte am Ende der Warteschlange einfügen. Typische Operationen auf einer Warteschlange sind:
| Operation | Erklärung | Aufwand |
|---|---|---|
| peek | Lesen der Datenstruktur am Kopf der Warteschlange ohne sie zu entfernen | O(1) |
| read | Lesen der vordersten Datenstruktur am Kopf und gleichzeitiges Entfernen | O(1) |
| write | Einfügen einer neuen Datenstruktur am Ende der Warteschlange | O(1) |
| search | Suche nach einer Datenstruktur in der Warteschlange und Rückgabe der Position | O(n) |
| empty | Testen ob die Warteschlange leer ist | O(1) |
Wichtig: Warteschlangen bieten keinen wahlfreien Zugriff auf alle ihre Elemente
Warteschlangen sind im realen Leben häufig anzutreffen wenn es sich um Prozesse handelt die alle Beteiligten demokratisch, transparent (fair?) behandeln soll:
- Fließband
- Rolltreppe
- Warten bei vielen Dienstleistern wird als FIFO organisiert
In der Informatik sind Warteschlangen immer dann anzutreffen wenn die Erhaltung einer Ankunftsreihenfolge eine Rolle spielt:
- Datenbanksperren
- Eingehende Webserveranforderungen
- Transaktionales Arbeiten (Sitzplatzreservierung)
Implementierung
Warteschlange sind Spezialfälle von Listen. Im Unterschied zu einer Liste erlauben sie nur das Einfügen von Objekten am Ende und das Entfernen am Kopf der Warteschlange:
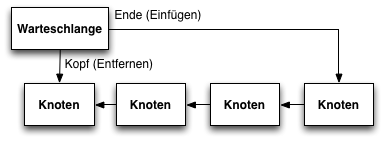
Ringpuffer
Warteschlangen die auf einfach oder zweifach verketteten Knoten beruhen sind sehr flexibel. Sie sind jedoch auch ineffizient da bei jedem Aufruf neue Knotenobjekte mit dem aufwendigen new() Operator erzeugt werden müssen.
Dies kann durch die Verwendung von ausreichend großen Ringpuffern vermieden werden, da hier die Knotenobjekte nur einmalig angelegt werden müssen. Diese Ringpuffer werden durch ein Feld R mit einer festen Größe n implementiert. Beim Erreichen des Endes des Feldes wird dieses durch ein Fortsetzen am Beginn des Feldes zum Ring "zusammengebogen".
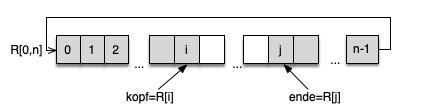
Hierzu benötigt man:
- einen Zeiger auf das Ende der Warteschlange (im Beispiel R[j])
- einen Zeiger auf den Kopf der Warteschlange (Im Beispiel R[i])
Beim Einfügen und Entfernen von Elementen werden beim Verrücken der Zeiger der Restwert nach der Division durch die Größe des Felds verwendet um nicht einen Feldüberlauf zu Erzeugen. Beim Einfügen eines neuen Elements in den Ringpuffer wird das neue Ende in Java wie folgt berechnet:
ende = (ende-1)%n;
Der Kopf wird nach dem Entfernen eines Elements wie folgt berechnet:
kopf = (kopf-1)%n;
Wichtig: Ringpuffer haben eine feste Größe. Es muss explizit eine Ausnahmebehandlung implementiert werden, wenn die Warteschlange über die Größe n des Feldes wächst.
- 9199 views
Implementierung
Unter "Implementierung" steht, dass Warteschlangen nur das Einfügen und Entfernen von Objekten am Ende der Warteschlange erlauben.
Nach dem FIFO-Prinzip müsste aber das Entfernen am Kopf der Warteschlange geschehen und nicht am Ende, damit auch das zuerst eingefügte Element als erstes wieder entfernt wird.
- Log in to post comments
Stimmt, irgendwie schon
Danke für den Hinweis. Ich habe das Skript angepasst. Kopf und Ende wurde hier etwas lax verwendet. Ich habe das Diagramm angepasst und nur noch eine Verzeigerung in eine Richtung eingemalt. Hierdurch sollte es keine Zweifel mehr geben.
- Log in to post comments
Ringpuffer Grafik
Ist es richtig so, dass der kopf=r[j] und das ende auch =r[j] ist?
Sind beim Ringpuffer Anfang und Ende identisch, wenn das Feld sein Ende erreicht hat?
Dachte, dass das nicht so wäre, weshalb mich die Grafik da gerade etwas verwirrt.
- Log in to post comments
Vielen Dank!
Toll beobachtet. Habe den Fehler im Diagramm korrigiert. Vielen Dank.
- Log in to post comments
Bäume
BäumeBäume werden in vielen Bereichen der Informatik verwendet, da Suchen und Einfügen sehr effizient erfolgen können
| Operation | Erklärung | Aufwand | Schlimmster Fall |
|---|---|---|---|
| Einfügen/Löschen | Ändern des Baums | O(log(n)) | O(n) |
| Suchen | Suchen eines Elements | O(log(n)) | O(n) |
| Nächstes Element | Finden des nächsten Elements | O(1) | O(1) |
Da naiv implementierte Bäume degenerieren können und dann die Aufwände einer Liste haben, werden in der Vorlesung einige, wenige Optimierungen diskutiert. Diese Optimierung unterbinden den schlimmsten Fall eines Aufwands mit der Ordnung O(n).
Bäume sind hierarchische Datenstrukturen die aus einer verzweigten Datenstruktur bestehen. Bäume bestehen aus Knoten und deren Nachfolgern.
Jeder Knoten in einem Baum hat genau einen Vorgängerknoten. Der einzige Knoten für den das nicht gilt, ist der Wurzelknoten (engl. root) er hat keinen Vorgänger. Der Wurzelknoten stellt den obersten Knoten dar. Von dieser Wurzel aus kann man von Knoten zu Knoten zu jedem Element des Baums gelangen.
| Rekursive Definition eines Baums |
|---|
| Ein Baum besteht aus Unterbäumen und diese setzen sich bis zu den Blattknoten wieder aus Unterbäumen zusammen. |
Die Baumstruktur wird in Ebenen unterteilt.
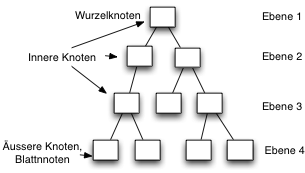
Die Tiefe eines Baumes ergibt sich aus der maximalen Anzahl der Ebenen.
Vollständige Bäume
| Vollständige Bäume |
|---|
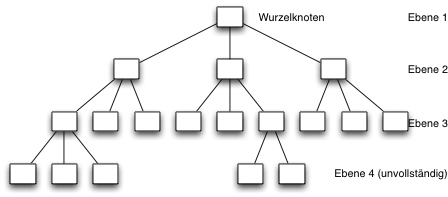
| Ein Baum ist vollständig wenn alle Ebenen ausser der letzten Ebene vollständig mit Knoten gefüllt sind. |
Im folgenden Beispiel wird ein Baum gezeigt, der maximal drei Nachfolgerknoten pro Konten besitzen kann:
Binärbäume
Binärbäume bestehen aus Knoten mit maximal 2 Nachfolgerknoten. Die maximale Anzahl Knoten pro Ebene ist 2(k-1) Knoten in der Ebene k.
Streng sortierte Binärbäume
| Streng sortierte Binärbäume |
|---|
|
Für jeden Baumknoten gilt:
|
Beispiel eines streng sortierten Binärbaums:
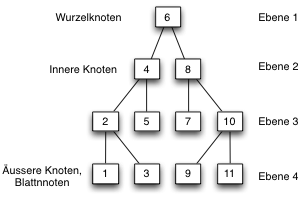
Suchen
Sortierte Binärbäume eignen sich sehr gut zum effektiven Suchen, da mit jedem Knoten die Auswahl der Kandidaten in der Regel halbiert wird.
Das Suchen in einem sortierten Baum geschieht nach dem folgenden, rekursiven Prinzip:
- Beginne mit dem Wurzelknoten
- Vergleiche den gesuchten Wert mit dem Wert des Knoten und beende die Suche wenn der Wert übereinstimmt.
- Suche im linken Teilbaum weiter wenn der gesuchte Wert kleiner als der aktuelle Knoten ist.
- Suche im rechten Teilbaum weiter wenn der gesuchte Wert größer als der Wert des aktuellen Knoten ist.
Bemerkung: Effektives Suchen ist nur in gutartigen (balancierten) Bäumen möglich. Gutartige Bäume haben möglichst wenig Ebenen. Schlechte Bäume zum Suchen sind degenerierte Bäume die im schlimmsten Fall pro Ebene nur einen Knoten besitzen. Solche degenerierten Bäume verhalten sich wie Listen.
Gutartige Bäume haben daher eine Tiefe T= ld(n+a) was auch dem Aufwand zum Suchen O (ld(n)) entspricht. Schlechte Bäume haben eine Tiefe T = n was zu einem Suchaufwand wie bei Listen, also O(n) führt.
Beispielprogramm
|
Das folgende Programm erlaubt es manuell einen Binärbaum aus Ganzzahlen aufzubauen. DownloadDas Programm steht als jar Datei zur Verfügung und kann nach dem Download wie folgt gestartet werden: java -jar BaumGUI.jar Es erlaubt das Einfügen und Entfernen von Blattknoten: |
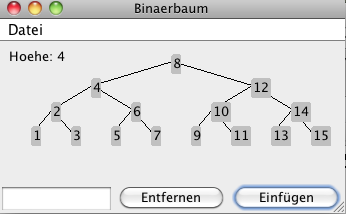 |
Alternative: Die Universität San Francisco hat eine sehr schöne webbasierte Visualisierung.
- 7932 views
AVL Bäume (Ausgeglichene Bäume)
AVL Bäume (Ausgeglichene Bäume)Binärbäume werden benutzt da sie ein sehr effizientes Suchen mit einem Aufwand von O(logN) erlauben solange sie balanciert sind. In extremen Fällen kann die Suche nach Knoten jedoch zu einem Aufwand von O(N) führen falls der Baum degeneriert ist.
Die im vorhergehenden Abschnitt vorgestellten Bäume verwenden in ihren Implementierungen der Einfüge- und Entferneoperation naive Verfahren. Diese naive Verfahren können dazu führen, dass ein Baum sehr unbalanciert werden kann.
Erste Vorschläge zur Vermeidung dieses Problems gehen auf die 1962 gemachten Vorschläge von Adelson-Velskij und Landis zurück. Sie schlugen höhenbalancierte AVL Bäume vor.
AVL Bäume
| AVL Baum |
|---|
|
Ein binärer Baum ist höhenbalanciert bzw AVL ausgeglichen wenn für jeden Knoten im Baum gilt:
|
Beispiele von AVL Bäumen die der obigen Definition genügen sind im folgenden Diagramm zu sehen
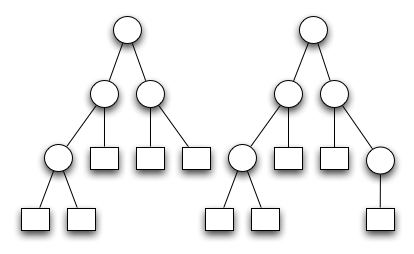
Der nachfolgende Baum ist kein AVL Baum. Der rechte Knoten in der zweiten Ebene von oben hat einen linken Unterbaum der Höhe 1 und einen rechten Unterbaum der Höhe 3.
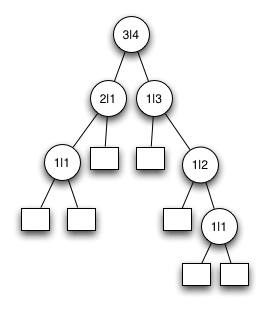
Dieser Baum müsste umorganisiert werden um ein AVL Baum zu werden.
Zum Verwalten von AVL Bäumen berechet man jedoch nicht immer wieder die Höhe der Teilbäume.
Es ist einfacher einen Balanchefaktor zu jedem inneren Knoten mitzuführen der die Differenz der Höhe vom linken und rechtem Teilbaum verwaltet.
| Balancefaktor bal(p) eines AVL Baums |
|---|
|
bal(p) = (Höhe rechter Teilbaum von p) - (Höhe linker Teilbaum von p) bal(p)∈{-1,0,1} |
Im folgenden Beispiel sind die Balancefaktoren für die inneren Knoten eingetragen:
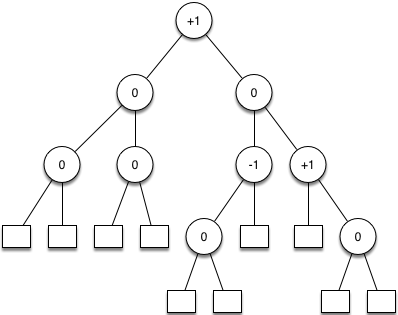
AVL Bäume müssen beim Einfügen und Entfernen von Knoten unter Umständen neu balanciert werden. Der Vorteil besteht jedoch in dem sehr vorhersagbaren Verhalten mit dem Aufwand von O(logN) bei Operationen auf dem Baum.
Tipp: Bauen Sie sich Ihren eigen AVL Baum. Die Universität hat eine web basierte Visualisierung von AVL Bäumen.
- 12067 views
Definition AVL-Baum, 2. Abb.
Kann es sein, dass bei den korrekten AVL-Bäumen unten rechts ein Kästchen fehlt? Dort ist bei einem Kreis lediglich ein Kästchen.
- Log in to post comments
Bruderbäume
BruderbäumeBruderbäume kann man als expandierte AVL Bäume verstehen.
Bruderbäume bekommen durch gezieltes Einfügen unärer Knoten eine konstante Tiefe für alle Blätter. Sie sind höhenbalancierte Bäume. Mit ihnen lässt sich garantieren, dass man mit dem gleichen Suchaufwand auf alle Blätter des Baums zugreifen kann.
Bruderbäume unterscheiden sich von den Binärbäumen dadurch, dass die inneren Knoten mindesten einen Sohn haben.
Bruderbäume haben ihren Namen von dem Fakt, dass für die Söhne eines Knoten untereinander (die Brüder) bestimmte Regeln gelten.
| Bruder |
|---|
| Zwei Knoten heißen Brüder wenn sie denselben Vater (Vorgängerknoten) haben. |
Ein binärer Baum ist ein Bruderbaum wenn das folgende gilt:
| Bruderbaum |
|---|
|
Ein Baum heißt Bruderbaum wenn die folgenden Bedingungen gelten:
|
Beispiele
Im folgenden Diagramm ist der rechte Baum ist kein Bruderbaum da es auf der zweiten Ebene von oben zwei unäre Bruder gibt.
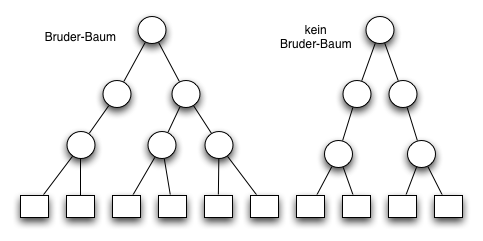
Im Diagramm unten ist der rechte Baum kein Bruderbaum weil die beiden Bruderknoten in der zweiten Ebene von oben unäre Brüder sind.
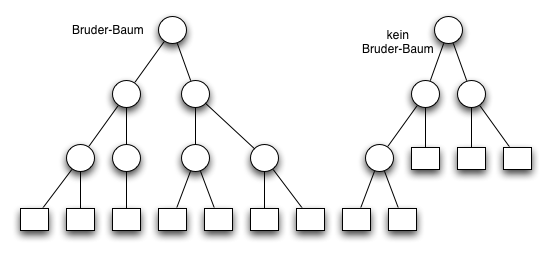
Bemerkung
Bei Bruderbäumen müssen bei Bedarf innerer Knoten eingefügt werden um die Bruderbedingungen zu erfüllen. Bruderbäume sind daher Bäume bei denen die zu verwaltenden Datenstrukturen nicht notwendigerweise in den inneren Knoten verwaltet werden können.
- 7803 views
Anzahl Söhne bei Bruderbäumen
Folgende, sich scheinbar widersprechende Aussagen entstammen Ihrem Skript. Was ist nun korrekt?
"Bruderbäume unterscheiden sich von den Binärbäumen dadurch, dass die inneren Knoten auch nur einen Sohn haben dürfen."
"Ein Baum heißt Bruderbaum wenn die folgenden Bedingungen gelten:
Jeder innere Knoten hat einen oder zwei Söhne."
- Log in to post comments
Gut beobachtet
Danke für den Kommentar.
Innere Knoten in Bruderbäumen müssen mindesten einen Sohn haben.
- Log in to post comments
Übungen (Bäume)
Übungen (Bäume)Balancierte und unbalancierte Bäume
Das folgende Programm erlaubt es manuell einen streng geordneten Binärbaum aus Ganzzahlen aufzubauen.
Das Programm steht als jar Datei zur Verfügung und kann nach dem Download wie folgt gestartet werden:
java -jar BaumGUI.jar
Balancierter Baum
Benutzen Sie das Beispielprogramm und erzeugen sie einen balancierten Baum mit 15 Knoten und der Höhe 4 wie zum Bsp.:

In welcher Reihenfolge müssen die Werte eingegeben werden?
Degenerierter Baum
Erzeugen Sie einen degenerierten Baum mit 5 Knoten und der Höhe 5:
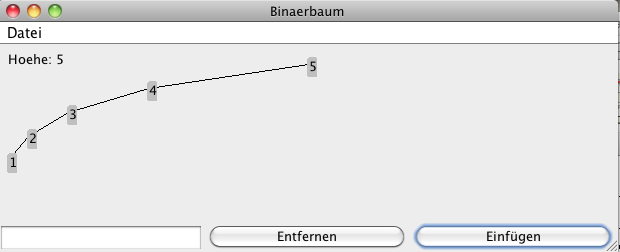
Welche Eingabefolgen von Zahlen erzeugen eine Liste degenerierten Teilbäumen?
Implementierung einer Binärbaums
Alle Klassen zu dieser Übung sind auch über github verfügbar.
Implementieren Sie einen streng geordneten Binärbaum in dem man ganze Zahlen Einfügen und Löschen kann.
Es ist nicht notwendig einen balancierten Baum oder AVL Baum zu implementieren.
Vervollständigen Sie die 3 drei fehlenden Methoden:
- s2.baum.Baumknoten
- Methode hoehe() : Implementieren Sie eine rekursive Methode zum bestimmen der Höhe des Baums (1.ter Schritt)
- s2.baum.Binaerbaum
- Methode einfuegen(teilBaum, Knoten) (2.ter Schritt)
- Tipps
- Betrachten Sie zuerst Sonderfälle (fehlen von Söhnen)
- Welchen Teilbaum müssen Sie modifizieren wenn der neue Knoten kleiner als die aktuelle Wurzel ist?
- Welchen Teilbaum müssen Sie modifizieren wenn der neue Knoten größer als die aktuelle Wurzel ist?
- Fügen Sie keinen Knoten mit einem Wert ein, der schon existiert!
- Tipps
- Methode loeschen(teilBaum, Knoten) (3.ter Schritt)
- Tipps
- Was müssen Sie tun wen der aktuelle Knoten gelöscht werden muss?
- Was müssen Sie tun wenn der zu löschende Knoten die Wurzel des gesamten Baums ist?
- Tipps
- Methode einfuegen(teilBaum, Knoten) (2.ter Schritt)
Übersetzen Sie alle Klassen. Starten Sie die Anwendung mit
$ java s2.baum.BaumGUI
Testen Sie die Anwendung mit der automatisierten Generierung mit dem Befehl
$ java s2.baum.BaumGUI magic
Hinweis: Die Implementierung des Algorithmus zum Entfernen von Knoten ist sehr viel aufwendiger da viele Randbedingungen geprüft werden müssen. Implementieren Sie zu Beginn nur das Einfügen von Knoten und Testen Sie zuerst das Einfügen. Die aktuelle Trivialimplementierung zum Entfernen erlaubt das Übersetzen und Ausführen der Anwendung ohne das Knoten entfernt werden.
UML Diagramm der beteiligten Klassen:
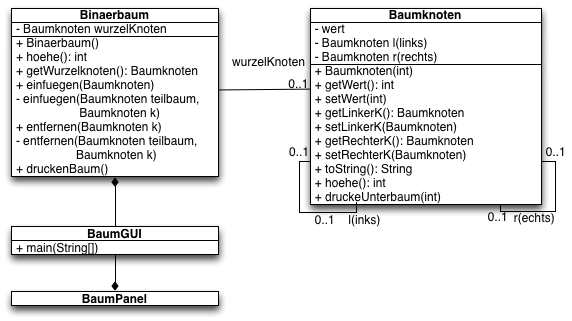
Notwendige Vorarbeiten
Erzeugen Sie die Infrastruktur für das folgenden Paket s2.baum
Klasse s2.baum.Baumknoten
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class Baumknoten {
private int wert;
//private final int maxWert= Integer.MAX_VALUE;
private final int maxWert= 99;
public int getWert() {
return wert;
}
public void setWert(int wert) {
this.wert = wert;
}
/**
* Verwalte linken Knoten
*/
private Baumknoten l;
/**
* verwalte rechten Knoten
*/
private Baumknoten r;
public Baumknoten(int i) {wert=i;}
/**
* Liefere linken Knoten zurück
* @return linker Knoten
*/
public Baumknoten getLinkerK() {
return l;
}
/**
* Setze linken Knoten
* @param k Referenz auf linken Knoten
*/
public void setLinkerK(Baumknoten k) {
l = k;
}
/**
* Liefere rechten Knoten zurück
* @return rechter Knoten
*/
public Baumknoten getRechterK() {
return r;
}
/**
* Setze rechten Knoten
* @param k rechter Knoten
*/
public void setRechterK(Baumknoten k) {
r = k;
}
/**
* Drucken einen Unterbaum und rücke entsprechend bei Unterbäumen ein
* @param einruecken
*/
public void druckeUnterbaum(int einruecken) {
if (l != null) {
l.druckeUnterbaum(einruecken + 1);
}
for (int i = 0; i < einruecken; i++) {
System.out.print(".");
}
System.out.println(toString());
if (r != null) {
r.druckeUnterbaum(einruecken + 1);
}
}
/**
* Berechne Höhe des Baums durch rekursive Tiefensuche
* @return
*/
public int hoehe() {
System.out.println("Implementieren Sie Baumknoten.hoehe() als rekursive Methode");
return -1;
}
/**
* Generiere eine Zufallsbelegung für den gegebenen Knoten
* Die Funktion darf nicht mehr nach Einfügen in den Baum
* aufgerufen werden, da der neue Wert zu einer inkorrekten Ordnung führt
*/
public void generiereZufallswert() {
wert= (int)(Math.random()*(double)maxWert);
}
/**
* Erlaubt den Zahlenwert als Text auszudrucken
* @return
*/
public String toString() { return Integer.toString(wert);}
}
Klasse s2.baum.Binaerbaum
package s2.baum;
/**
*
* @author sschneid
*/
public class Binaerbaum {
private Baumknoten wurzelKnoten;
public Baumknoten getWurzelknoten() {return wurzelKnoten;}
/**
* Füge einen neuen Baumknoten in einen Baum ein
* @param s
*/
public void einfuegen(Baumknoten s) {
if (wurzelKnoten == null) {
// Der Baum ist leer. Füge Wurzelknoten ein.
wurzelKnoten = s;
}
else // Der Baum ist nicht leer. Normales Vorgehen
einfuegen(wurzelKnoten,s);
}
/**
* Füge einen gegebenen Knoten s in einen Teilbaum ein.
* Diese Methode ist eine rekursive private Methode
* Da der neue Knoten die Wurzel des neuen Teilbaums bilden kann,
* wird eventuell ein Zeiger auf einen neuen Teilbaum zurückgeliefert
* Randbedingung:
* * Es wird kein Knoten mit einem Wert eingefügt der schon existiertz
* @param teilbaum
* @param s
*/
private void einfuegen(Baumknoten teilbaum, Baumknoten s) {
System.out.println("Implementieren Sie die Methode Binaerbaum:einfuegen()");
}
/**
* Öffentliche Methoden zum Entfernen eines Baumknotens
* @param s
*/
public void entfernen(Baumknoten s) {
wurzelKnoten = entfernen(wurzelKnoten,s);}
/**
* Private, rekursive Methode zum Entfernen eines Knotens aus einem
* Teilbaum. Es kann ein neuer Teilbaum enstehen wennn der Wurzelknoten
* selbst entfernt werden muss. Der neue Teilbaum wird daher wieder mit
* ausgegeben
* @param teilbaum Teilbaum aus dem ein Knoten entfernt werden soll
* @param s der zu entfernende Knoten
* @return Der verbleibende Restbaum. Es kann auch Null für einen leeren Baum ausgegeben werden
*/
private Baumknoten entfernen(Baumknoten teilbaum, Baumknoten s) {
System.out.println("Implementieren Sie die Methode Binaerbaum:entfernen()");
return teilbaum;
}
/**
* Berechnung der Hoehe des Baums
* @return Hoehe des Baums
*/
public int hoehe() {
if (wurzelKnoten == null) return 0;
else return wurzelKnoten.hoehe();
}
/**
* Rückgabe des Namens
* @return
*/
public String algorithmus() {return "Binaerbaum";}
public void druckenBaum() {
System.out.println("Tiefe:" + hoehe());
if (wurzelKnoten != null) wurzelKnoten.druckeUnterbaum(0);
System.out.println("A-----------A");
}
}
Klasse s2.baum.BaumGUI
package s2.baum;
import java.awt.BorderLayout;
import java.awt.Container;
import java.awt.GridLayout;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JMenu;
import javax.swing.JMenuBar;
import javax.swing.JMenuItem;
import javax.swing.JPanel;
import javax.swing.JTextField;
/**
*
* @author s@scalingbits.com
*/
public class BaumGUI implements ActionListener {
final private JFrame hf;
final private JButton einfButton;
final private JButton entfButton;
final private JTextField eingabeText;
final private JMenuBar jmb;
final private JMenu jm;
final private JMenuItem exitItem;
final private BaumPanel myBaum;
final private Binaerbaum b;
public BaumGUI(Binaerbaum bb) {
b = bb;
JLabel logo;
//ButtonGroup buttonGroup1;
JPanel buttonPanel;
// Erzeugen einer neuen Instanz eines Swingfensters
hf = new JFrame("BaumGUI");
// Gewünschte Größe setzen
// 1. Parameter: horizontale Größe in Pixel
// 2. Parameter: vertikale Größe
hf.setSize(220, 230);
// Beenden bei Schliesen des Fenster
hf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
// Erzeugen der Buttons und Texteingabefeld
eingabeText = new JTextField("17");
einfButton = new JButton();
einfButton.setText("Einfügen");
entfButton = new JButton();
entfButton.setText("Entfernen");
// Registriere die eigene Instanz
// zum Reagieren auf eine Aktion der beiden Buttons
einfButton.addActionListener(this);
entfButton.addActionListener(this);
// Einfügen der drei Komponenten in ein Panel
// Das Gridlayout führt zum Strecken der drei Komponenten
buttonPanel = new JPanel(new GridLayout(1, 1));
buttonPanel.add(eingabeText);
buttonPanel.add(entfButton);
buttonPanel.add(einfButton);
// Erzeugen des Panels zum Malen des Baums
myBaum = new BaumPanel(b);
// setze Titel des Frame
hf.setTitle(b.algorithmus());
// Erzeuge ein Menueeintrag zum Beenden des Programms
jmb = new JMenuBar();
jm = new JMenu("Datei");
exitItem = new JMenuItem("Beenden");
exitItem.addActionListener(this);
jm.add(exitItem);
jmb.add(jm);
hf.setJMenuBar(jmb);
Container myPane = hf.getContentPane();
myPane.add(myBaum, BorderLayout.CENTER);
myPane.add(buttonPanel, BorderLayout.SOUTH);
hf.pack();
hf.setVisible(true);
hf.setAlwaysOnTop(true);
}
/**
* Diese Methode wird bei allen Aktionen der Menüleiste oder
* der Buttons aufgerufen
* @param e
*/
public void actionPerformed(ActionEvent e) {
Object source = e.getSource();
int wert = 0;
try {
if (source == entfButton) { //Entfernen aufgerufen
wert = Integer.parseInt(eingabeText.getText());
b.entfernen(new Baumknoten(wert));
myBaum.fehlerText("");
myBaum.repaint();
eingabeText.setText("");
}
if (source == einfButton) { // Einfügen aufgerufen
wert = Integer.parseInt(eingabeText.getText());
b.einfuegen(new Baumknoten(wert));
myBaum.fehlerText("");
myBaum.repaint();
eingabeText.setText("");
}
if (source == exitItem) { // Beenden aufgerufen
System.exit(0);
}
} catch (java.lang.NumberFormatException ex) {
// Fehlerbehandlung bei fehlerhafter Eingabe
myBaum.fehlerText("Eingabe '" + eingabeText.getText() + "' ist keine Ganzzahl");
myBaum.repaint();
eingabeText.setText("");
}
}
public static void main(String[] args) {
BaumGUI sg = new BaumGUI(new Binaerbaum());
if ((args.length > 0) && (args[0].equalsIgnoreCase("magic"))) {
sg.magicMode(15);
}
}
public void magicMode(int anzahl) {
Baumknoten[] gz = new Baumknoten[anzahl];
for (int i = 0; i < gz.length; i++) {
gz[i] = new Baumknoten(0);
gz[i].generiereZufallswert();
}
try {
for (int i = gz.length - 1; i >= 0; i--) {
eingabeText.setText(gz[i].toString());
b.einfuegen(gz[i]);
Thread.sleep(800);
myBaum.repaint();
}
for (int i = 0; i < gz.length; i++) {
eingabeText.setText(gz[i].toString());
b.entfernen(gz[i]);
Thread.sleep(800);
myBaum.repaint();
}
} catch (InterruptedException e) {
}
}
}
Klasse s2.baum.BaumPanel
package s2.baum;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import javax.swing.JPanel;
/**
*
* @author s@scalingbits.com
*/
public class BaumPanel extends JPanel{
final private Binaerbaum b;
final private int ziffernBreite = 10 ; // Breite einer Ziffer in Pixel
final private int ziffernHoehe = 20; // Hoehe einer Ziffer in Pixel
private String fehlerString;
public BaumPanel(Binaerbaum derBaum) {
fehlerString = "";
b = derBaum;
setPreferredSize(new Dimension(600,200));
setDoubleBuffered(true);
}
/**
* Setzen des Fehlertexts des Fehlertexts
* @param s String mit Fehlertext
*/
public void fehlerText(String s) {fehlerString = s;}
/**
* Methode die das Panel überlädt mit der Implementierung
* der Baumgraphik
* @param g
*/
public void paintComponent(Graphics g) {
super.paintComponent(g);
int maxWidth = getWidth();
int maxHeight = getHeight();
Baumknoten k = b.getWurzelknoten();
if (k != null) { // Male Wurzelknoten falls existierend
g.setColor(Color.black);
g.drawString("Hoehe: " + b.hoehe(), 10, 20);
g.drawString(fehlerString, 10, 40);
paintKnoten(g,k,getWidth()/2, 20);
}
else {
g.setColor(Color.RED);
g.drawString("Der Baum ist leer. Bitte Wurzelknoten einfügen.",10,20);
}
}
/**
* Malen eines Knotens und seines Unterbaums
* @param g Graphicshandle
* @param k zu malender Knoten
* @param x X Koordinate des Knotens
* @param y Y Koordinate des Knotens
*/
public void paintKnoten(Graphics g,Baumknoten k, int x, int y) {
int xOffset = 1; // offset Box zu Text
int yOffset = 7; // offset Box zu Text
String wertString = k.toString(); // Wert als Text
int breite = wertString.length() * ziffernBreite;
int xNextNodeOffset = ((int)java.lang.Math.pow(2,k.hoehe()-1))*10;
int yNextNodeOffset = ziffernHoehe*6/5; // Vertikaler Offset zur naechsten Kn.ebene
if (k.getLinkerK() != null) {
// Male linken Unterbaum
g.setColor(Color.black); // Schriftfarbe
g.drawLine(x, y, x-xNextNodeOffset, y+yNextNodeOffset);
paintKnoten(g,k.getLinkerK(),x-xNextNodeOffset,y+yNextNodeOffset);
}
if (k.getRechterK() != null) {
// Male rechten Unterbaum
g.setColor(Color.black); // Schriftfarbe
g.drawLine(x, y, x+xNextNodeOffset, y+yNextNodeOffset);
paintKnoten(g,k.getRechterK(),x+xNextNodeOffset,y+yNextNodeOffset );
}
// Unterbäume sind gemalt. Male Knoten
g.setColor(Color.LIGHT_GRAY); // Farbe des Rechtecks im Hintergrund
g.fillRoundRect(x-xOffset, y-yOffset, breite, ziffernHoehe, 3, 3);
g.setColor(Color.black); // Schriftfarbe
g.drawString(wertString, x+xOffset, y+yOffset);
}
}
Baumschule...
Fragen zu Binärbäumen
Welche der beiden Bäume sind korrekte, streng sortierte Binärbäume?
Welche sind keine streng sortierten Binärbäume und warum?
Streng sortierter Binärbaum 1
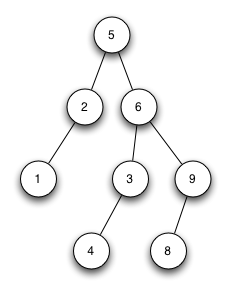
Streng sortierter Binärbaum 2
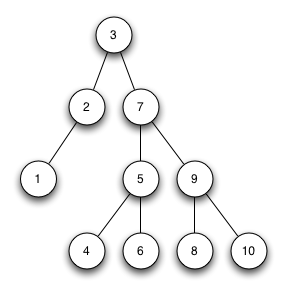
AVL Bäume
Welche der beiden AVL-Bäume sind korrekte AVL-Bäume?
Welche Bäume sind keine korrekten AVL Bäume und warum?
AVL-Baum 1
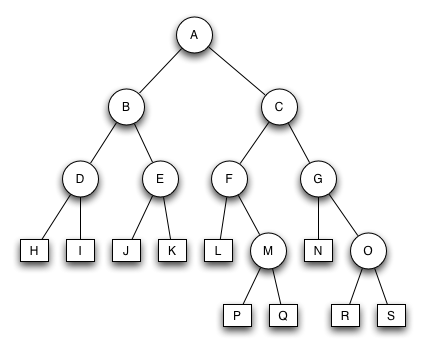
AVL Baum 2
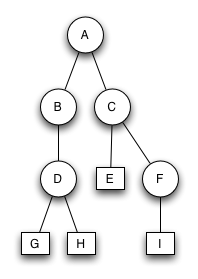
Bruder-Baum
Welche der beiden Bäume sind keine korrekten Bruder-Bäume?
Warum sind sie keine Bruderbäume?
Bruder-Baum 1
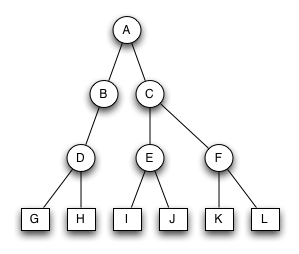
Bruder-Baum 2
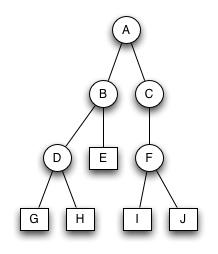
Bruder-Baum 3
- 12892 views
Lösungen (Bäume)
Lösungen (Bäume)Balancierte und unbalancierte Bäume
Balancierter Baum
Eingabe: 8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15
Es sind auch andere Lösungen möglich.
Degenerierte Baum
Eingabemöglichkeiten
- 5, 4, 3, 2, 1
- 1, 2, 3, 4, 5
Sortierte Folgen, gleich ob sie fallend oder steigend sortiert sind, führen bei einfachen binären Bäumen zu degenerierten Bäumen mit großer Höhe.
Implementierung eines Binärbaums
Klasse s2.baum.Baumknoten
Informelle Beschreibung der Algorithmen
Höhe eines Baums
- Bestimme Höhe des linken Unterbaums
- Gibt es einen linkenUnterbaum?
- Nein: Höhe links =0
- Ja: Höhe links= Höhe linker Unterbaum
- Gibt es einen linkenUnterbaum?
- Bestimme Höhe des rechten Unterbaum
- Gibt es einen rechten Unterbaum?
- Nein: Höhe rechts = 0
- Ja: Höhe rechts = Höhe rechter Unterbaum
- Gibt es einen rechten Unterbaum?
- Bestimme den höchsten der beiden Unterbäume
- Höhe des Baumes= 1 + Höhe höchster Unterbaum
Quellcode
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class Baumknoten {
private int wert;
//private final int maxWert= Integer.MAX_VALUE;
private final int maxWert= 99;
public int getWert() {
return wert;
}
public void setWert(int wert) {
this.wert = wert;
}
/**
* Verwalte linken Knoten
*/
private Baumknoten l;
/**
* verwalte rechten Knoten
*/
private Baumknoten r;
public Baumknoten(int i) {wert=i;}
/**
* Liefere linken Knoten zurück
* @return linker Knoten
*/
public Baumknoten getLinkerK() {
return l;
}
/**
* Setze linken Knoten
* @param k Referenz auf linken Knoten
*/
public void setLinkerK(Baumknoten k) {
l = k;
}
/**
* Liefere rechten Knoten zurück
* @return rechter Knoten
*/
public Baumknoten getRechterK() {
return r;
}
/**
* Setze rechten Knoten
* @param k rechter Knoten
*/
public void setRechterK(Baumknoten k) {
r = k;
}
/**
* Drucken einen Unterbaum und rücke entsprechend bei Unterbäumen ein
* @param einruecken
*/
public void druckeUnterbaum(int einruecken) {
if (l != null) {
l.druckeUnterbaum(einruecken + 1);
}
for (int i = 0; i < einruecken; i++) {
System.out.print(".");
}
System.out.println(toString());
if (r != null) {
r.druckeUnterbaum(einruecken + 1);
}
}
/**
* Berechne Höhe des Baums durch rekursive Tiefensuche
* @return
*/
public int hoehe() {
int lmax = 1;
int rmax = 1;
int max = 0;
if (l != null) lmax = 1 + l.hoehe();
if (r != null) rmax = 1 + r.hoehe();
if (rmax > lmax) return rmax;
else return lmax;
}
/**
* Generiere eine Zufallsbelegung für den gegebenen Knoten
* Die Funktion darf nicht mehr nach EInfügen in den Baum
* aufgerufen werden, da der neue Wert zu einer inkorrekten Ordnung führt
*/
public void generiereZufallswert() {
wert= (int)(Math.random()*(double)maxWert);
}
/**
* Erlaubt den Zahlenwert als Text auszudrucken
* @return
*/
public String toString() { return Integer.toString(wert);}
}Klasse s2.baum.Binaerbaum
Informelle Beschreibung der Algorithmen
Einfügen von Knoten
- Ist der Wert des neuen Knoten gleich der Wurzel meines Baums?
- Ja: Fertig. Es wird nichts eingefügt
- Nein:
- Ist der Wert kleiner als mein Wurzelknoten?
- Ja: Der neue Knoten muss links eingefügt werden
- Gibt es einen linken Knoten?
- Nein: Füge Knoten als linken Knoten ein
- Ja: Rufe Einfügemethode rejursiv auf...
- Gibt es einen linken Knoten?
- Nein: Der neue Knoten muss rechts eingefügt werden
- Gibt es einen rechten Knoten?
- Nein: Füge Knoten als rechten Knoten ein
- Ja: Rufe Einfügemethode rekursiv auf...
- Gibt es einen rechten Knoten?
- Ja: Der neue Knoten muss links eingefügt werden
- Ist der Wert kleiner als mein Wurzelknoten?
Quellcode
package s2.baum;
/**
*
* @author s@scalingbits.com
*/
public class BinaerbaumLoesung {
private Baumknoten wurzelKnoten;
public Baumknoten getWurzelknoten() {return wurzelKnoten;}
/**
* Füge einen neuen Baumknoten in einen Baum ein
* @param s
*/
public void einfuegen(Baumknoten s) {
if (wurzelKnoten == null) {
// Der Baum ist leer. Füge Wurzelknoten ein.
wurzelKnoten = s;
}
else // Der Baum ist nicht leer. Normales Vorgehen
einfuegen(wurzelKnoten,s);
}
/**
* Füge einen gegebenen Knoten s in einen Teilbaum ein.
* Diese Methode ist eine rekursive private Methode
* Da der neue Knoten die Wurzel des neuen Teilbaums bilden kann,
* wird eventuell ein Zeiger auf einen neuen Teilbaum zurückgeliefert
* Randbedingung:
* * Es wird kein Knoten mit einem Wert eingefügt der schon existiertz
* @param teilbaum
* @param s
*/
private void einfuegen(Baumknoten teilbaum, Baumknoten s) {
if (!(s.getWert()==teilbaum.getWert())) {
// Nicht einfuegen wenn Knoten den gleichen Wert hat
if (s.getWert()<teilbaum.getWert()) {
// Im linken Teilbaum einfuegen
if (teilbaum.getLinkerK() != null)
einfuegen(teilbaum.getLinkerK(),s);
else teilbaum.setLinkerK(s);
}
else // Im rechten Teilbaum einfuegen
if (teilbaum.getRechterK() != null)
einfuegen(teilbaum.getRechterK(),s);
else teilbaum.setRechterK(s);
}
}
/**
* Öffentliche Methoden zum Entfernen eines Baumknotens
* @param s
*/
public void entfernen(Baumknoten s) {
wurzelKnoten = entfernen(wurzelKnoten,s);}
/**
* Private, rekursive Methode zum Entfernen eines Knotens aus einem
* Teilbaum. Es kann ein neuer Teilbaum enstehen wennn der Wurzelknoten
* selbst entfernt werden muss. Der neue Teilbaum wird daher wieder mit
* ausgegeben
* @param teilbaum Teilbaum aus dem ein Knoten entfernt werden soll
* @param s der zu entfernende Knoten
* @return Der verbleibende Restbaum. Es kann auch Null für einen leeren Baum ausgegeben werden
*/
private Baumknoten entfernen(Baumknoten teilbaum, Baumknoten s) {
Baumknoten result = teilbaum;
if (teilbaum != null) {
if (teilbaum.getWert()==s.getWert()) {
// der aktuelle Knoten muss entfernt werden
Baumknoten altRechts = teilbaum.getRechterK();
Baumknoten altLinks = teilbaum.getLinkerK();
if (altRechts != null) {
result = altRechts;
if (altLinks != null) einfuegen(result, altLinks);
}
else
if (altLinks!=null) result = altLinks;
else result = null;
}
else if (teilbaum.getWert()<s.getWert()) {
Baumknoten k = teilbaum.getRechterK();
teilbaum.setRechterK(entfernen(k,s));
}
else {
Baumknoten k = teilbaum.getLinkerK();
teilbaum.setLinkerK(entfernen(k,s));
}
}
return result;
}
/**
* Berechnung der Hoehe des Baums
* @return Hoehe des Baums
*/
public int hoehe() {
if (wurzelKnoten == null) return 0;
else return wurzelKnoten.hoehe();
}
/**
* Rückgabe des Namens
* @return
*/
public String algorithmus() {return "Binaerbaum";}public void druckenBaum() {
System.out.println("Tiefe:" + hoehe());
if (wurzelKnoten != null) wurzelKnoten.druckeUnterbaum(0);
System.out.println("A-----------A");
}
}
Baumschule...
Fragen zu Binärbäumen
Welche der beiden Bäume sind korrekte, streng sortierte Binärbäume?
Welche sind keine streng sortierten Binärbäume und warum?
Streng sortierter Binärbaum 1
Der Baum ist kein streng sortierter Binärbaum. Knoten 3 müsste rechter Sohn von Knoten 2 sein. Knoten 4 müsste rechter Sohn von Knoten 3 sein.

Streng sortierter Binärbaum 2
Der Baum ist ein streng sortierter Binärbaum.

AVL Bäume
Welche der beiden AVL-Bäume sind korrekte AVL-Bäume?
Welche Bäume sind keine korrekten AVL Bäume und warum?
AVL-Baum 1
Der Baum ist ein AVL-Baum. Alle Blätter sind auf nur zwei unterschiedlichen Ebenen angeordnet.

AVL Baum 2
Der Baum ist kein AVL Baum. Das Fehlen eines zweiten Sohns von Knoten B führt zu einem Unterschied von zwei Ebenen im Baum.

Bruder-Baum
Welche der beiden Bäume sind keine korrekten Bruder-Bäume?
Warum sind sie keine Bruderbäume?
Bruder-Baum 1
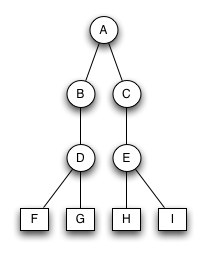
Der Baum ist ein Bruder-Baum. Alle Blätter sind auf der untersten Ebene. Der einzige unäre Knoten B hat einen binären Bruderknoten.

Bruder-Baum 2
Der Baum ist kein Bruder-Baum. Der Blattknoten E ist nicht auf der untersten Ebene.

Bruder-Baum 3
Der Baum ist kein Bruder-Baum. Knoten B und C sind unäre Brüder. Einer von ihnen müsste binär sein.
Knoten B und C sind überflüssig. Nach ihrem Entfernen entsteht wieder ein Bruder-Baum.

- 11059 views
Lernziele (Datenstrukturen)
Lernziele (Datenstrukturen)|
|
Am Ende dieses Blocks können Sie:
|
Lernzielkontrolle
Sie sind in der Lage die folgenden Fragen zu beantworten: Fragen zu Datenstrukturen
Feedback

- 3872 views
typo
Einführung
[...] Zur Lösung dieser Anforderung müssen die folgenden Aspekte betrachtet werden:
[...]