4.4 Iteration und Rekursion
4.4 Iteration und RekursionIn den vorangegangen Abschnitten wurden verschiedene Schleifenkonstrukte vorgestellt mit denen man Codestrecken wiederholt durch laufen kann. Dieses Verfahren nennt man Iteration.
Methoden können aber nicht nur andere Methoden aufrufen, sie können auch sich selbst aufrufen. Dieses Verfahren nennt man Rekursion. Beide Verfahren sind von der Theorie her gleichwertig. Sie können wechselseitig eingesetzt werden. Im folgenden Beispiel wird die Multiplikation durch fortgesetzte Addition nach dem folgenden Prinzip iterativ und rekursiv gelöst.
Rekursive Algorithmen wenden das "Teile und Herrsche" Prinzip an indem Sie ein gegebenes Problem zerlegen in
- ein trivial lösbares Problem
- ein Restproblem welches gleich dem ursprünglichen Problem strukturiert ist (und einfacher ist!)
|
Die rekursive Methode fib() basiert auf den folgenden Definition von Fibonaccifolgen fib(0) = 0 (ein trivial lösbares Problem) fib(1) = 1 (ein trivial lösbares Problem) für alle n > 1 fib(n) = fib(n-1) + fib(n-2) (das einfachere Restproblem) |
Fibonacciberechnung |
Beispielprogramm:
package s1.block4;
public class Fibonacci {
public static long fib(int f) {
long ergebnis=0;
switch (f) {
case 0: { ergebnis = 0;break;} // Triviales Problem. Keine Rekursion
case 1: { ergebnis = 1;break;} // Triviales Problem. Keine Rekursion
default: { // Die Rekursion
ergebnis = fib(f - 1) + fib(f - 2);
break;
} // Ende default
} // Ende switch
return ergebnis;
} // Ende Methode
public static void main(String[] args) {
int a = 10; //Anzahl der berechneten Fibonaccizahlen
System.out.println("Fibonacciberechnung von fib(0) bis fib(" + a + ")");
for (int i=0; i<=a; i++)
System.out.println("fib("+i+")= " + fib(i));
} // Ende main()
} // Ende Klasse| Anmerkung: Diese naive Implementierung ist sehr ineffizient. Das Programm berechnet zu jeder Fibonaccizahl die beiden vorhergehenden Zahlen neu. Der Aufwand zur Berechnung der Fibonaccizahlen steigt daher exponentiell mit der Potenz 2. Dies macht den hier gewähltenAlhorithmus, zur Berechnung für größerer Fibonaccizahlen, ungeeignet. | 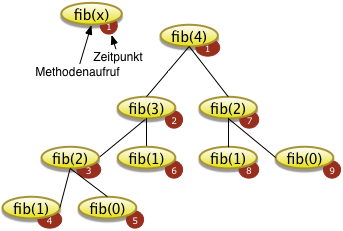 |
Beispiel: Quersummenberechnung
Die Methode berechne() berechnet eine Quersumme iterativ mit Hilfe einer while Schleife. Die Methode berechneRekursiv() berechnet das Ergebnis rekursiv (mit Selbstaufruf).
package s1.block4;
public class Quersumme {
/**
* Hauptprgramm zum Berechnen der Quersumme
* @param args wird nicht benutzt
*/
public static void main (String[] args) {
long eing = 12345678;
long ausg = berechne(eing);
System.out.println ("Ausgabe:" + ausg + "; Eing: " +eing);
System.out.println("Berechne rekursiv");
ausg = berechneRekursiv(eing);
System.out.println ("Ausgabe:" + ausg + "; Eing: " +eing);
}
/**
* Iterative Berechnung einer Quersumme mit einer while Schleife
* @param eing
* @return ausgabe
*/
public static long berechne(long eing){
long a = 0;
while (eing>0) { //Abbruch bei Null
a += eing%10; //Aufaddieren der letzen Stelle
eing /= 10; //Teilen der Zahl durch 10
}
return a;
}
/**
* Rekursive Berechnung einer Quersumme
* @param eing
* @return ausgabe
*/
public static long berechneRekursiv (long eing){
long a = 0;
if (eing>0) a = (eing%10)+berechneRekursiv(eing/10);
else a = 0; // Triviale Loesung. Nicht rekursiv.
return a;
}
}
Beispiel: Die Türme von HanoiDie Türme von Hanoi sind ein einfaches Solitärspiel bei dem die folgenden Regeln gelten:
Siehe Wikipedia für weiterführende Erklärung und Animation. Die Strategie
|
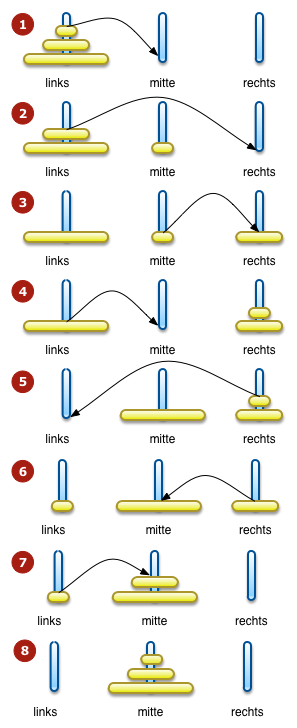
Lösung für 3 Scheiben
|
Implementierung der Türme von Hanoi in Java
package s1.block4;
public class Hanoi {
public static void bewegeScheiben(int scheiben,
String von,
String nach,
String hilfsstab){
if (scheiben >0) {
bewegeScheiben(scheiben-1, von, hilfsstab,nach);
System.out.println(scheiben + ".te Scheibe von " + von + " nach " + nach );
bewegeScheiben(scheiben-1, hilfsstab, nach, von);
}
}
public static void main(String[] args) {
bewegeScheiben(3, "links", "mitte", "rechts");
}
}
Ablauf des Programmes
Konsolenausgabe1.te Scheibe von links nach mitte 2.te Scheibe von links nach rechts 1.te Scheibe von mitte nach rechts 3.te Scheibe von links nach mitte 1.te Scheibe von rechts nach links 2.te Scheibe von rechts nach mitte 1.te Scheibe von links nach mitte |
Rekursive Aufrufe der Methoden |
- 18578 views