Fragen zu Algorithmen

Fragen zu Algorithmen

Bonusfrage aus dem Web...

javafrage Tue, 03/21/2017 - 17:34
  • 2628 views

1 Quicksort

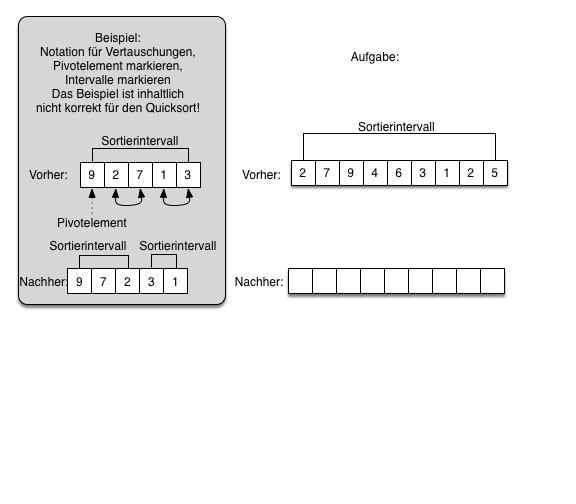
1 Quicksort

Führen Sie einen Durchlauf des Quicksorts zum Teilen des ersten Intervalls manuell durch. Teilen Sie ein gegebenes Sortierintervall (siehe Aufgabe „Vorher“) nach den Regeln des Quicksorts in zwei Unterintervalle die noch sortiert werden müssen.

  • Sortieren Sie aufsteigend 
  • Wählen Sie das Pivotelement ganz rechts im Intervall. Das Pivotelement soll zum kleineren Intervall gehören.
  • Markieren Sie das Pivotelement im „Vorher“ Diagramm mit einem Pfeil von unten (siehe Beispiel).
  • Wenden Sie die Regeln des Quicksorts an. Zeichnen Sie zweiseitige Pfeile im "Vorher" Diagram ein, um die notwendigen Vertauschungen zu markieren.
  • Zeichnen Sie mit einem zweiseitigen Pfeil die nötige Vertauschung des Pivotelements im "Vorher" Diagramm ein.
  • Tragen Sie alle neuen Werte im "Nachher" Diagramm ein.
  • Zeichnen sie die beiden neuen zu sortierenden Intervalle mit eckigen Linien im „Nacher“ Diagramm ein.

Quicksort Array

Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 8 Minuten
javafrage Thu, 02/02/2012 - 09:12
  • 5384 views

2 Quicksort, Pivotelement

2 Quicksort, Pivotelement

Wählt man beim Quicksort das Pivotelement immer am gleichen Rand des Intervals, so gibt es Zahlenreihen die nur sehr ineffizient sortiert werden.
Für welche Zahlenreihen trifft dies zu? Geben Sie ein Beispiel an.

Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 2 Minuten

Antwort zu Frage 1: Quicksort

Quicksort Lösung

 

javafrage Thu, 02/02/2012 - 18:02
  • 5421 views

Anonymous (not verified)

Tue, 06/02/2015 - 14:13

Permalink

Wir sind nach mehreren anläufen jedes mal auf die Lösung "2 1 3 4 5 9 8 7 6" gekommen. Warum ist bei Ihnen die 3 und 4 bzw. die 9 und 8 vertauscht?

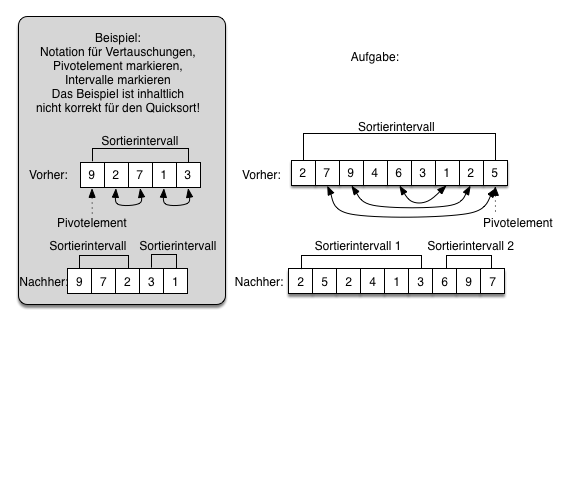
Für die Behandlung des Pivotelements gibt es unterschiedliche akzeptable Strategien. In der Musterlösung wurde wie folgt vorgegangen:

  • Beginne links im Sortierinterval und merke das erste Element welches größer-gleich als 5 ist.
    • Dies ist die 9. Halte mit der Suche an
  • Beginne rechts im Sortierinterval und suche (fallend) das erste Element welches kleiner als 5 ist.
    • Dies ist die 4. Halte mit der Suche an.
  • Tausche 4 mit 9

Setze die Strategie des Suchens von links und rechts fort

  • Vergleiche von links kommend das nächste Element (die 8) ob es größer gleich 5 ist und halte dann an.
  • Vergleiche von rechts kommend, fallend das nächste Element (die 3) ob sie kleiner ist als die 5 und halte dann an
  • Tausche 8 mit 3

Jetzt kommt es zum "Endspiel". Die beiden Zeiger der Suche von links und rechts treffen sich. Hier gibt es wieder Freiheitsgrade.

  • Man kann die 6 mit der 5 tauschen und dann die 5 aus den zukünftigen Suchintervallen ausschließen
  • Falls der Wert auf der fünften Position kleiner als das Pivotelement gewesen wäre hätte man es stehen lassen und die fünfte Position in das neue linke Sortierintervall einbezogen.

 

3 Ungünstige Zahlenreihen für den Quicksort

3 Ungünstige Zahlenreihen für den Quicksort

Warum funktioniert das „Teile und Herrsche“ Prinzip des Quicksorts bei unvorteilhaften Zahlenreihen nicht gut?

Beispiele sind die folgenden Zahlenreihen

  • 1,2,3,4,5
  • 5,4,3,2,1

Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 2 Minuten

Antwort zu Frage 2: Quicksort, Pilotelement

Aufsteigende oder fallende Zahlenfolgen. z. Bsp. 1,2,3,4,5 oder 5,4,3,2,1

javafrage Fri, 02/03/2012 - 10:55
  • 4611 views

4 Heapsort, Baumpräsentation, Heapbedingung

4 Heapsort, Baumpräsentation, Heapbedingung

Zeigen Sie wie der logische Baum eines Heapsorts für ein gegebenes Feld von Schlüsseln aussieht.
Tragen Sie die Schlüssel und den Feldindex (die Feldposition) der Feldrepräsentation in die Heappräsentation unten ein.

Im Beispiel unten ist auf der Position 1 der Schlüssel 9 zu finden.
Tragen Sie Positionen und Schlüssel in das vorgegebene Baumdiagramm ein:

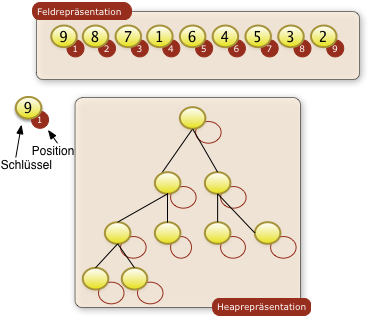
Diagramm eines Heapsorts

Gilt die Heapbedingung für diese Folge? Markieren Sie Knoten die die Heapbedingung verletzen.

Die Antworten finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 5+2 Minuten

Antwort zu Frage 3: Ungünstige Zahlenreihen für den Quicksort

Weil keine ähnlich großen Teilintervalle entstehen.

Im schlimmsten Fall wird das Teilintervall immer nur um ein Element verkleinert.

Der Aufwand ist dann (n-1)+O(n-2)+...+O(3)+O(2)=O(n2) (Arithmetische Reihe)

Der Aufwand zum Bearbeiten der Teilintervalle kann dann im schlimmsten Fall O(n2) anstatt O (n*log(n)) wie bei ähnlich großen Teilintervallen sein.

javafrage Tue, 01/01/2013 - 16:28
  • 4478 views

5 Erklärung der Heapbedingung

5 Erklärung der Heapbedingung

Beschreiben in Worten was die „Heapbedingung“ des Heapsorts ist.

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 3 Minuten

Antwort zu Frage 4: Heapsort, Baumpräsentation, Heapbedingung

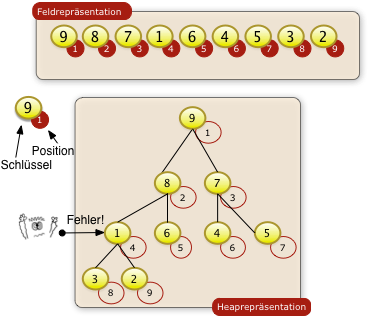
Diagramm eines Heapsorts

Die Heapbedingung gilt nicht für diese Folge. Sie ist für die Position 4 (Wert 1) verletzt.

javafrage Tue, 01/01/2013 - 17:34
  • 4451 views

Anonymous (not verified)

Tue, 04/26/2016 - 17:39

Permalink

hier gibt es einen Fehler mit dem Bild zur Lösung von 2.32
Die "Textantwort" ist aber eigentlich auch ausreichend

6 Komplexitätsbetrachtungen 1

6 Komplexitätsbetrachtungen 1

Welche Komplexität haben die gezeigten Javamethoden?

Gegeben ist das folgende Javaprogramm:

Nr. Quellcode Antwort
  
public class K1 {
private static int groesse = 1000;
public static void main(String[] args) {
  algorithmusBsp(groesse);
  algorithmus1(groesse);
  algorithmus2(groesse);
  algorithmus3(groesse);
  algorithmus4(groesse);
}
  nichts eintragen
 Bsp. 
static void algorithmusBsp(int n) {
  for (int i = 1; i < n; i++) {
    int k = i * 2;
  }
  for (int j = 1; j < n; j++) {
    int k = j * 3;
    }
}
 Beispiel:
Ofor1(n)+Ofor2(n) = O(n) 
1.  
static void algorithmus1(int n) {
  for (int i = 1; i < n; i++) {
    int k = i * 2;
  }
  for (int i = 1; i < 1000; i++) {
    int k = i +2;
  }
}
  
 2. 
static void algorithmus2(int n) {
  for (int i = 1; i < n; i++) {
    int p = n;
    for (int j = 1; j < p; j++) {
      int k = j - i;
    }
  }
}
 
 3. 
static void algorithmus3(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < n; j++) {
      for (int k = 1; k < n; k++) {
        int q = k - j - i;
      }
      int p=0;
        while (p<n) {
          p++;
          int r = n*p;
        }
    }
  }
}
 
 4. 
static void algorithmus4(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < 1000; j++) {
      algorithmus2(n);
    }
  }
}
 
  
}// Ende der Klasse
  Nichts eintragen

 

Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 8 Minuten

Antwort zu Frage 5: Erklärung der Heapbedingung

Das Feld soll aufsteigend sortiert werden.
Jeder Vaterknoten muss größer als beide Unterknoten sein oder auch: jeder Knoten mit dem Index i muss größer als existierende Knoten mit Index 2*i und 2*i+1 sein.

javafrage Mon, 02/13/2012 - 09:42
  • 4622 views

Anonymous (not verified)

Tue, 06/27/2017 - 11:32

Permalink

M.E. sind die Aussagen "Jeder Vaterknoten muss größer als beide Unterknoten sein." und "Jeder Knoten mit dem Index i muss größer als existierende Knoten mit Index 2*i und 2*i+1 sein." redundant. Könnten sie das bitte in der Antwort ersichtlich machen?

7 Komplexitätsbetrachtungen 2

7 Komplexitätsbetrachtungen 2

Tragen Sie die Aufwände O(n) für die gegeben Methoden des Javaprogramm ein.

Nr. Quellcode Antwort
  
public class K1 {
   private static int groesse = 1000;
 
   public static void main(String[] args) {
     algorithmusBsp(groesse);
     algorithmus1(groesse);
     algorithmus2(groesse);
     algorithmus3(groesse);
     algorithmus4(groesse);
   } 
  Nichts in dieses Feld eintragen!
 Bsp. 
  static void algorithmusBsp(int n) {
     for (int i = 1; i < n; i++)
        { int k = i * 2; }
     for (int j = 1; j < n; j++)
        { int k = j * 3;}
   }
 Beispiel:
Ofor1(n)+Ofor2(n) = O(n)
1. 
  static void algorithmus1(int n) {
     for (int i = 1; i < n; i++) {
       int k = i * 2;
     }
     int i = 0;
     while (i<1000) {
        i++;
       int k = i +2;
     }
  }
  
2. 
  static void algorithmus2(int n) {
     for (int i = 1; i < n; i++) {
       int p = n;
       for (int j = 1; j < p; j++) {
         for (int k = 1; k < n; k++) {
            int s = j*k – i;
         }
       }
     }
  }
  
3. 
  static void algorithmus3(int n) {
     for (int i = 1; i < n; i++) {
        for (int j = 1; j < n; j++) {
           int k= 0;
           while (k<n) {
              k++;
              int q = k - j - i;
           }
           int p=0;
           while (p<n) {
             p++;
             int r = n*p;
           }
       }
    }
 }
  
4. 
  static void algorithmus4(int n) {
     for (int i = 1; i < n; i++) {
        for (int j = 1; j < 1000; j++) {
           algorithmus2(n);
        }
     }
  }
  
  
 }// Ende der Klasse
  ---

 

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 8 Minuten

Antwort zu Frage 6: Komplexitätsbetrachtungen 1

Gegeben ist das folgende Javaprogramm:

Nr. Quellcode Antwort
  
public class K1 {
private static int groesse = 1000;
public static void main(String[] args) {
  algorithmusBsp(groesse);
  algorithmus1(groesse);
  algorithmus2(groesse);
  algorithmus3(groesse);
  algorithmus4(groesse);
}
  nichts eintragen
 Bsp. 
static void algorithmusBsp(int n) {
  for (int i = 1; i < n; i++) {
    int k = i * 2;
  }
  for (int j = 1; j < n; j++) {
    int k = j * 3;
    }
}
 Beispiel:
Ofor1(n)+Ofor2(n) = O(n) 
1.  
static void algorithmus1(int n) {
  for (int i = 1; i < n; i++) {
    int k = i * 2;
  }
  for (int i = 1; i < 1000; i++) {
    int k = i +2;
  }
}
 O(n)+O(1000)=O(n) 
 2. 
static void algorithmus2(int n) {
  for (int i = 1; i < n; i++) {
    int p = n;
    for (int j = 1; j < p; j++) {
      int k = j - i;
    }
  }
}
O(n)*O(n)=O(n2)
 3. 
static void algorithmus3(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < n; j++) {
      for (int k = 1; k < n; k++) {
        int q = k - j - i;
      }
      int p=0;
        while (p<n) {
          p++;
          int r = n*p;
        }
    }
  }
}
O(n)*O(n)*[O(n)+O(n)]=O(n3)
 4. 
static void algorithmus4(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < 1000; j++) {
      algorithmus2(n);
    }
  }
}

O(n)*[O(1000)*O(algorithmus2)]=

O(n)*O(algorithmus2)=O(n3)
  
}// Ende der Klasse
  Nichts eintragen
javafrage Wed, 01/09/2013 - 08:48
  • 3798 views

8 Komplexitätsbetrachtungen 3

8 Komplexitätsbetrachtungen 3

Welchen Aufwand O haben die Methoden algorithmus1() bis algorithmus8() des folgenden Programms abhängig vom Übergabeparameter n?

Gehen Sie davon aus, das der Java JIT (Just in Time Compiler) nichts optimiert.

Hinweis: Wie oft werden die jeweiligen Schleifen durchlaufen? Welche Durchläufe sind konstant, welche variabel?

package Kurs2.Sort;
public class Komplexität {
private static int groesse = 1000;
public static void main(String[] args) {
        algorithmus1(groesse);
        algorithmus2(groesse);
        algorithmus3(groesse);
        algorithmus4(groesse);
        algorithmus5(groesse);
        algorithmus6(groesse);
        algorithmus7(groesse);
    }
public static void algorithmus1(int n) {
        for (int i = 1; i < n; i++) {
            int k = i * 2;
        }
    }
public static void algorithmus2(int n) {
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < 1000; j++) {
                int k = j - i;
            }
        }
    }
public static void algorithmus3(int n) {
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < n; j++) {
                int k = j - i;
            }
        }
    }
public static void algorithmus4(int n) {
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < n; j++) {
                for (int k = 1; k < n; k++) {
                    int q = k - j - i;
                }
            }
        }
    }
public static void algorithmus5(int n) {
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < 1000; i++) {
                int k = j - i;
            }
            for (int j = 1; j < 1000; j++) {
                int k = j - i;
            }
        }
    }
public static void algorithmus6(int n) {
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < i; j++) {
                int k = j - i;
            }
        }
    }
public static void algorithmus7(int n) {
        for (int i = 1; i < 1000; i++) {
            int j = 0;
            while (j < 1000) {
                j++;
                int k = 2 * j;
            }
        }
    }

public static void algorithmus8(int n) {
        for (int i = 1; i < n; i++) {
            algorithmus1(n);
        }
    }

} // Ende der Klasse

 

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 16 Minuten

Antwort zu Frage 7:Komplexitätsbetrachtungen 2

Nr. Quellcode Antwort
  
public class K1 {
   private static int groesse = 1000;
 
   public static void main(String[] args) {
     algorithmusBsp(groesse);
     algorithmus1(groesse);
     algorithmus2(groesse);
     algorithmus3(groesse);
     algorithmus4(groesse);
   } 
  Nichts in dieses Feld eintragen!
 Bsp. 
  static void algorithmusBsp(int n) {
     for (int i = 1; i < n; i++)
        { int k = i * 2; }
     for (int j = 1; j < n; j++)
        { int k = j * 3;}
   }
 Beispiel:
Ofor1(n)+Ofor2(n) = O(n)
1. 
  static void algorithmus1(int n) {
     for (int i = 1; i < n; i++) {
       int k = i * 2;
     }
     int i = 0;
     while (i<1000) {
        i++;
       int k = i +2;
     }
  }
 Ofor1(n)+Ofor2(1000)= Ofor1(n)+Ofor2(1) = O(n)
2. 
  static void algorithmus2(int n) {
     for (int i = 1; i < n; i++) {
       int p = n;
       for (int j = 1; j < p; j++) {
         for (int k = 1; k < n; k++) {
            int s = j*k – i;
         }
       }
     }
  }
  Ofor1(n)*Ofor2(n)*Ofor3(n) = O(n3)
3. 
  static void algorithmus3(int n) {
     for (int i = 1; i < n; i++) {
        for (int j = 1; j < n; j++) {
           int k= 0;
           while (k<n) {
              k++;
              int q = k - j - i;
           }
           int p=0;
           while (p<n) {
             p++;
             int r = n*p;
           }
       }
    }
 }
 Ofor1(n)*Ofor2(n)*(Owhile1(n)+Owhile2(n))
Ofor1(n)*Ofor2(n)*2*Owhile(n)= 2*O(n3) = O(n3) 
4. 
  static void algorithmus4(int n) {
     for (int i = 1; i < n; i++) {
        for (int j = 1; j < 1000; j++) {
           algorithmus2(n);
        }
     }
  }
  Ofor(n)*Ofor2(1000)*Oalgorithmus2(n3) = O(n4)
  
 }// Ende der Klasse
  ---
javafrage Wed, 01/09/2013 - 09:32
  • 4094 views

Anonymous (not verified)

Wed, 06/27/2018 - 16:31

Permalink

In der Aufgabenstellung wird nur nach den Algorithmen 1-7 gefragt, in der Lösung sind alle vorhanden.

9 Binäre Suche

9 Binäre Suche

Fügen im folgenden Beispiel eine binäre Suche nach dem vorgegebenen Schlüssel durch. Zeichnen Sie die notwendigen Vergleiche mit Hilfe von Pfeilen wie im Beispiel der sequentiellen Suche ein:

Sequentielle und binäre Suche

Wieviele Vergleiche benötigen Sie bei der binären Suche in der obigen Folge mit 15 Elementen maximal bis der Schlüssel gefunden ist?

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 3+1 Minuten

Antwort zu Frage 8: Kompexitätsbetrachtungen 3

Quellcode Antworten mit Erklärung 
package Kurs2.Sort;
public class Komplexitaet;
  private static int groesse = 1000;

  public static void main(String[] args) {
    algorithmus1(groesse);
    algorithmus2(groesse);
    algorithmus3(groesse);
    algorithmus4(groesse);
    algorithmus5(groesse);
    algorithmus6(groesse);
    algorithmus7(groesse);
  }
  
  public static void algorithmus1(int n) {
    for (int i = 1; i < n; i++) {
      int k = i * 2;
    }
  }
 Die for-Schleife wird n mal durchlaufen: O(n)  
  public static void algorithmus2(int n) {
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < 1000; j++) {
       int k = j - i;
      }
    }
  }

Die innere for-Schleife wird 1000 mal durchlaufen:

  • O(1000) = Oinnere(1)

Die äussere for-Schleife wird n mal durchlaufen:

  • O(n)*Oinnere(1)=Oaeussere(n)

Gesamtkomplexität: O(n)

 
  public static void algorithmus3(int n) {
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < n; j++) {
        int k = j - i;
      }
   }
  }
 Die innere for-Schleife wird n mal durchlaufen: 
  • Oinnere(n)

Die äussere for-Schleife wird n mal durchlaufen:

  • O(n)*Oinnere(n)=Oaeussere(n2)

Gesamtkomplexität: O(n2)

 
  public static void algorithmus4(int n) {
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < n; j++) {
        for (int k = 1; k < n; k++) {
          int q = k - j - i;
        }
      } 
    }
  }

Die innere for-Schleife wird n mal durchlaufen:

  • Oinnere(n)

Die mittlere for-Schleife wird n mal durchlaufen:

  • O(n)*Oinnere(n) = Omittlere(n2)

Die äussere for-Schleife wird n mal durchlaufen:

  • O(n)*Omittlere(n2)= Oaeussere(n3)

Gesamtkomplexität: O(n3)
 

 
  public static void algorithmus5(int n) {
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < 1000; j++) {
        int k = j - i;
      }
      for (int j = 1; j < 1000; j++) {
        int k = j - i;
      }
    }
  }

Jede der inneren Schleifen wird 1000 mal durchlaufen und hat damit einen konstanten Aufwand

  • Oinnere2(1000)+Oinnere2(1000)= Oinnere2(1)+Oinnere2(1)=Oinnen(1)

Die äussere Schleife wird n mal durchlaufen:

  • O(n)*Oinnen(1)=Oaeussere(n)

Gesamtkomplexität: O(n)

 
  public static void algorithmus6(int n) {
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < i; j++) {
        int k = j - i;
      }
    }
  }

Jede der inneren Schleifen wird i mal durchlaufen:

  • Oinnen(i)

Die äussere Schleife wird n mal durchlaufen:

  • O(n)*Oinnen(i)

Beide Schleifen haben gemeinsam die Durchläufe 1+2+3... +n = (n-1)n/2 = (n2-n)2

  • O(n)*Oinnen(i)=(O(n2)-O(n))/O(2)=O(n2)/O(1)=Oaussen(n2)

Gesamtkomplexität: O(n2)
Bemerkung: Das Zusammenwirken geschachtelter Schleifen ist nicht trivial. Es müssen alle relevanten Variablen aufgelöst und es muss eine Summenformel entwickelt werden.

 
   public static void algorithmus7(int n) {
    for (int i = 1; i < 2000; i++) {
      int j = 0;
      while (j < 1000) {
        j++;
        int k = 2 * j;
      }
    }
  }

Die while-Schleife wird 1000 mal durchlaufen. Ihr Aufwand ist konstant:

  • Owhile(1000)=Owhile(1) 

Die for-Schleife wird wird 2000 mal durchlaufen. Ihr Aufwand ist konstant:

  • O(2000)*Owhile(1)=O(1)*Owhile(1)=Ofor(1)

Gesamtkomplexität: O(1)

 
  public static void algorithmus8(int n) {
    for (int i = 1; i < n; i++) {
      algorithmus1(n);
    }
  }

Die Methode algorithmus1() hat den Aufwand O(n). Siehe weiter oben.

Die for-Schleife wird n mal durchlaufen:

  • O(n)*O(n)=Ofor(n2)

Gesamtkomplexität: O(n2)

 
} // Ende der Klasse

 
javafrage Mon, 03/17/2014 - 08:19
  • 4605 views

Anonymous (not verified)

Thu, 05/04/2017 - 06:20

Permalink

Wie kann ich den an der Aufgabenstellung erkennen das es sich um eine sortierte Folge handelt?

Grüße

Für alle i von Null bis zum höchsten Element der Folge f gilt: fi < fi+1

10 Aufwand binäre Suche und sequentielle Suche

10 Aufwand binäre Suche und sequentielle Suche
  • Welchen Aufwand O() hat die binäre Suche?
  • Welchen Aufwand O() hat die sequentielle Suche?

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 2 Minuten

Antwort zu Frage 9: Binäre Suche

Beispiel einer binären Suche

Man benötigt maximal 4 Vergleiche.

javafrage Mon, 03/17/2014 - 08:27
  • 4102 views

Anonymous (not verified)

Mon, 05/11/2020 - 19:02

Permalink

Bei der Binären Suche liegt ein Fehler vor. Es sind lediglich 3 Vergleiche die gemacht werden.

Im ersten Schritt 15 - ist richtig
Im zweiten Schritt muss allerdings die 19 markiert werden anstelle der 21.
Im dritten Vergleichsschritt kommt man dann direkt auf die 23

Viele Grüße!

11 Komplexitätsbetrachtungen 4

11 Komplexitätsbetrachtungen 4

Tragen Sie die Aufwände O(n) für die gegeben Methoden des Javaprogramm ein.

Nr. Quellcode Antwort
  
public class K1 {
   private static int groesse = 1000;
 
   public static void main(String[] args) {
     algorithmusBsp(groesse);
     algorithmus1(groesse);
     algorithmus2(groesse);
     algorithmus3(groesse);
     algorithmus4(groesse);
   } 
  Nichts in dieses Feld eintragen!
 Bsp. 
  static void algorithmusBsp(int n) {
     for (int i = 1; i < n; i++)
        { int k = i * 2; }
     for (int j = 1; j < n; j++)
        { int k = j * 3;}
   }
 Beispiel:
Ofor1(n)+Ofor2(n) = O(n)
1. 
  static void algorithmus1(int n) {
    for (int i = 1; i < n; i++) {
      int p = n;
      for (int j = 1; j < p; j++) {
        for (int k = 1; k < n; k++) {
          int s = j*k – i;
        } // end for
      } // end for
    } // end for
  }
  
2. 
  static void algorithmus2(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < n; j++) {
      int k= 0;
      while (k<n) {
         k++;
         int q = k - j - i;
      }
      int p=0;
      while (p<n) {
          p++;
          int r = n*p;
       } // end while
    } // end for
  } // end for
}
  
3. 
  static void algorithmus3(int n) {
  for (int i = 1; i < n; i++) {
   for (int j = i; j < n; j++) {
    int k=0;
    while (k<1000000) {  
      k++;
      int r = i*j*k;
 } // end while
   } // end for
  } // end for
}
  
4. 
  static void algorithmus4(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < 1000; j++) {
      algorithmus1(n);
    }
  }
}
  
  
 }// Ende der Klasse
  ---

 

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 8 Minuten

Antwort zu Frage 10: Aufwand binäre und sequentielle Suche

  • Aufwand O() der binären Suche: O(log(n))
  • Aufwand O() der sequentiellen Suche: O(n)
javafrage Sun, 03/01/2015 - 11:18
  • 3220 views

12 Bubblesort

12 Bubblesort

Der BubbleSort besteht aus einer äusseren Schleife in der das zu sortierende Intervall jeweils verkleinert wird.
In einer inneren Schleife wird das größte Element als « Bubble » bestimmt. Führen Sie einen solchen Durchlauf einer inneren Schleife an der unten gezeigten Folge durch. Sortieren sie aufsteigend.

Markieren Sie alle notwendigen Vergleiche und Vertauschungen.
Fügen Sie alle Werte in das Diagramm ein
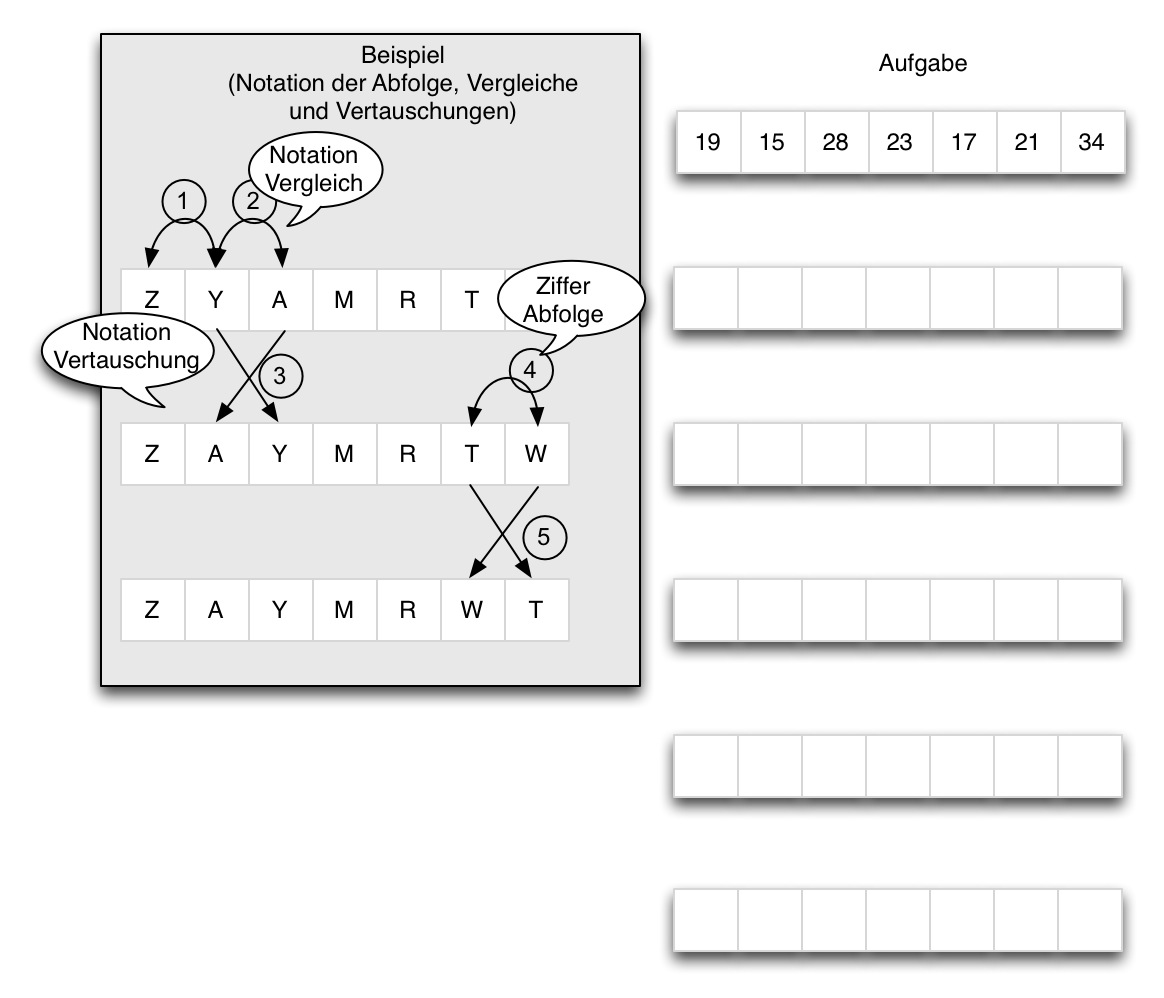
 Diagramm einer Folge die im Bubblsort sortiert werden soll

Welchen Aufwand O() hat der Bubblesort?

In welchem Fall ist ein aufsteigend sortierender Bubblesort ein sehr effizienter Algorithmus?

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 8+1+1 Minuten

Antwort zu Frage 11: Komplexitätsbetrachtungen 4

Nr. Quellcode Antwort
  
public class K1 {
   private static int groesse = 1000;
 
   public static void main(String[] args) {
     algorithmusBsp(groesse);
     algorithmus1(groesse);
     algorithmus2(groesse);
     algorithmus3(groesse);
     algorithmus4(groesse);
   } 
  Nichts in dieses Feld eintragen!
 Bsp. 
  static void algorithmusBsp(int n) {
     for (int i = 1; i < n; i++)
        { int k = i * 2; }
     for (int j = 1; j < n; j++)
        { int k = j * 3;}
   }
 Beispiel:
Ofor1(n)+Ofor2(n) = O(n)
1. 
  static void algorithmus1(int n) {
    for (int i = 1; i < n; i++) {
      int p = n;
      for (int j = 1; j < p; j++) {
        for (int k = 1; k < n; k++) {
          int s = j*k – i;
        } // end for
      } // end for
    } // end for
  }
 Ofor1(n)*Ofor2(n)*Ofor3(n) = O(n3) 
2. 
  static void algorithmus2(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < n; j++) {
      int k= 0;
      while (k<n) {
         k++;
         int q = k - j - i;
      }
      int p=0;
      while (p<n) {
          p++;
          int r = n*p;
       } // end while
    } // end for
  } // end for
}

Ofor1(n)*Ofor2(n)*(Owhile1(n)+Owhile2(n)) =

Ofor1(n)*Ofor2(n)*O(n) =

O(n3) 
3. 
  static void algorithmus3(int n) {
  for (int i = 1; i < n; i++) {
   for (int j = i; j < n; j++) {
    int k=0;
    while (k<1000000) {  
      k++;
      int r = i*j*k;
 } // end while
   } // end for
  } // end for
}

Ofor1(n)*Ofor2(n)*(Owhile1(1000)) =

Ofor1(n)*Ofor2(n) =

O(n2) 
4. 
  static void algorithmus4(int n) {
  for (int i = 1; i < n; i++) {
    for (int j = 1; j < 1000; j++) {
      algorithmus1(n);
    }
  }
}

Ofor1(n)*Ofor2(1000)*Oalgorithmus1(n) =

Ofor1(n)*O(n3) =

O(n4) 
  
 }// Ende der Klasse
  ---
javafrage Sat, 03/21/2015 - 13:04
  • 3660 views

13 Komplexitätsbetrachtungen 5

13 Komplexitätsbetrachtungen 5

Ein Algorithmus A und B verarbeiten jeweils n Datensätzen.

  • Algorithmus A benötigt einmalig 50000000 Instruktionen mehr als Algorithmus B beim Starten. Ansonsten ist die Anzahl der Instruktionen pro Datensatz konstant.
  • Algorithmus B benötigt 4 mal mehr Instruktionen pro Datensatz als Algorithmus A

Leiten Sie die beiden Komplexitätsklassen der Algorithmen her.

Vergleichen Sie die beiden Komplexitätsklassen und geben Sie eine kurze Erklärung.

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 4+4 Minuten

Antwort zu Frage 12: Bubblesort

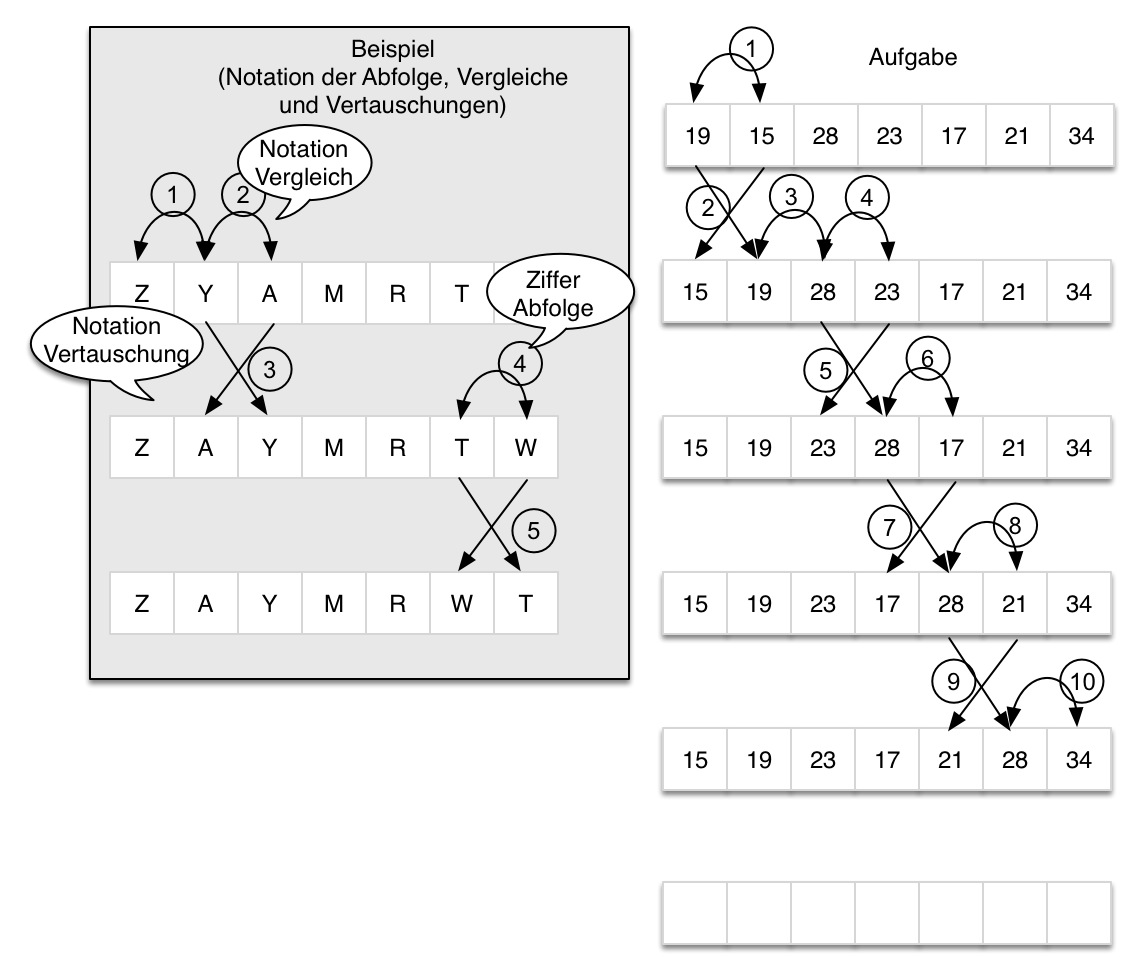
Bubblesort mit Musterlösung

Welchen Aufand O() hat der Bubblesort ?

O(n2)

In welchem Fall ist ein aufsteigend sortierender Bubblesort ein sehr effizienter Algorithmus?

Bei einer vorsortierten Folge

javafrage Mon, 12/07/2015 - 12:42
  • 2870 views

14 Sortiergrenze beim Insertionsort (Sortieren durch Einfügen)

14 Sortiergrenze beim Insertionsort (Sortieren durch Einfügen)

Was ist die Sortiergrenze in der Folge in der durch Sortieren durch Einfügen sortiert wird?

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 2 Minuten

Antwort zu Frage 13: Komplexitätsbetrachtungen 5

k sei der konstante Zeitaufwand der zum verarbeiten eines Datensatzes benötigt wird

OA (n) =O (5000000+k*n)=O (1)+O (n)=OA (n)

OB (n) =OA (4n)= OA (n)

Beide Algorithmen sind in der gleichen Komplexitätsklasse. Der zweite Algorithmus wird bei sehr kleinen Anzahlen etwas schneller sein.

holodoctor Sat, 03/25/2017 - 14:47
  • 5105 views

15 Sortieren durch Einfügen: Ein Beispiel

15 Sortieren durch Einfügen: Ein Beispiel

Die unten aufgeführte Folge im Diagramm wird aufsteigend sortiert und ist schon teilsortiert. Markieren Sie im Diagramm die Sortiergrenze mit einem Pfeil.

Führen Sie nun einen Durchlauf des Insertionsorts durch.

  • Vergleichen und Tauschen Sie den nächsten Wert solange bis er an der richtigen Stelle steht (3 Min.)
  • Markieren Sie die neue Sortiergrenze mit einem Pfeil (1 Min.)

Hinweis: Markieren Sie eine nötige Vertauschung wie im Beispiel gezeigt.
Tragen Sie dann die neuen Werte in die nächste Zeile ein.
Benutzen Sie dann eine neue Zeile.

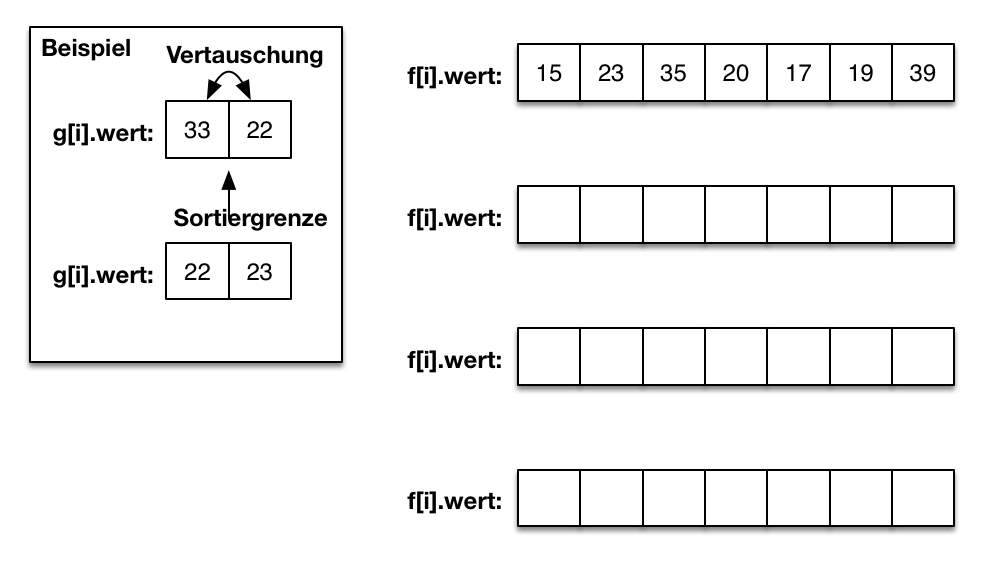
Übung Insertionssort

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 1+4 Minuten

Antwort zu Frage 14: Sortiergrenze beim Insertionsort (Sortieren durch Einfügen)

Die Grenze zwischen der unsortierten und der sortierten Folge

javafrage Sat, 03/25/2017 - 15:02
  • 3909 views

16 Fragen zum Sortieren durch Einfügen

16 Fragen zum Sortieren durch Einfügen

Ein paar Fragen zum Sortieren durch Einfügen...

  • Welchen Komplexitätsaufwand hat dieser Algorithmus?
  • Nennen Sie zwei Algorithmen aus der Vorlesung die eine bessere Aufwandsklasse besitzen.
  • Welchen Vorteil hat der Insertionsort immer gegenüber den beiden Algorithmen die eine bessere Komplexitätsklasse besitzen?

Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).

Niveau 2
Schwierigkeitsgrad mittel
Zeit 1+2+2 Minuten

Antwort zu Frage 15 Sortieren durch Einfügen: Ein Beispiel

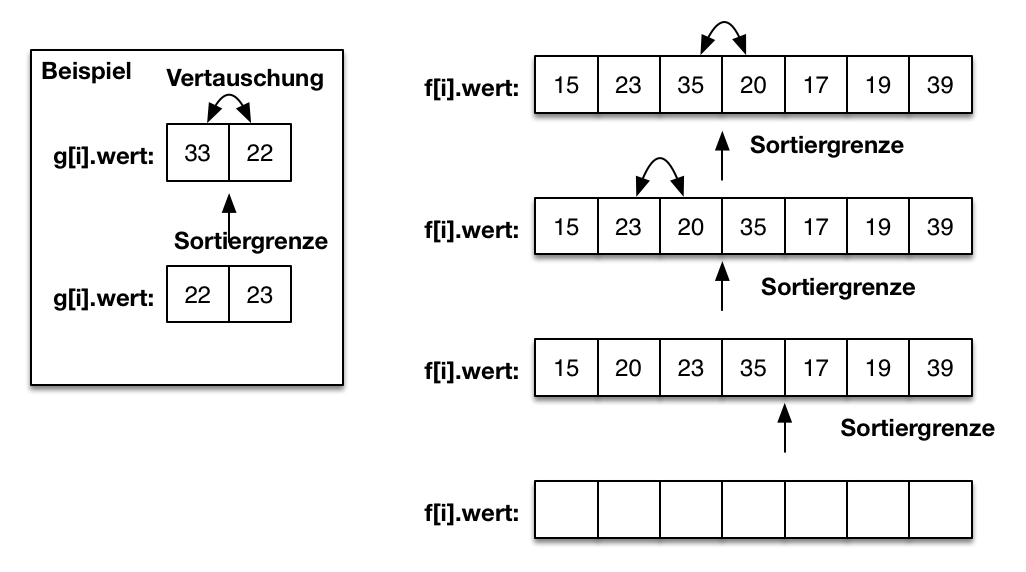
Lösung zur Aufgabe Soertieren durch EInfügen

Die Antwort zur aktuellen Frage finden Sie viel weiter unten

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Antwort zu Frage 16: Fragen zum Sortieren durch Einfügen

  • Durchschnittlicher Aufwand: Oinsertionsort(n) = O(n2)
  • Effizientere Sortierverfahren
    1. Quicksort
    2. Heapsort
  • Er ist stabil.
javafrage Sat, 03/25/2017 - 15:14
  • 42387 views

Anonymous (not verified)

Tue, 06/27/2017 - 09:13

Permalink

Die durchschnittliche Komplexität eines Insertion Sorts ist O(n^2). Wobei beste Komplexität O(n) ist (bei sortierten Listen) und schlechteste O(n^2).

Quelle: bigocheatsheet

Anmerkung: Evtl. liegt hier ein Darstellungsproblem in ihrer Lösung vor und O(n2) meint O(n^2).