1.2 Algorithmen

1.2 Algorithmen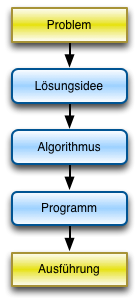
Vorgehen vom Problem zur AUsführung

Im Diagramm links wird das typische Vorgehensmodell gezeigt welches von einer Problemstellung zur einer ausführbaren Anwendung führt.

  1. Lösungsidee: Der erste Schritt zur Lösung der in der Vorlesung vorgestellten Probleme basiert auf einer Idee zur Lösung des Problems
  2. Algorithmus: Im nächsten Schritt wird die Lösungsidee zu einem Algorithmus verfeinert und ausgearbeitet
  3. Programm: Ein wesentlicher Teil der Vorlesung wird aus der Umsetzung eines Algorithmus in ein ausführbares Java-Programm bestehen

Üblicherweise treten in jeder Phase Fehler auf, die ein Zurückgehen und Verbessern der Ergebnisse einer früheren Phase erfordern.

Algorithmus

  • Vorgehensbeschreibung, Handlungsanweisung
  • Alltagsbeispiele:
Kochrezept, Bastelanleitung, Partitur
  • Mathematische Beispiele:
    • 
Euklids ggT-Bestimmung, geometrische Konstruktionen
  • Name abgeleitet von Muhammed al-Chwarizmis Buch „Über das Rechnen mit indischen Ziffern“ (um 825)
  • Erster Computeralgorithmus:
1843 von Ada Lovelace für Charles Babbages Analytical Engine (Maschine wurde nicht vollendet)

Anforderungen an einen gültigen Algorithmus

  • Er verlangt gültige Eingaben und liefert definierte Ausgaben, durch die seine Korrektheit überprüft werden kann
  • Er umfasst endlich viele Einzelschritte und besteht aus hinreichend elementaren Anweisungen
  • Er ist in realistischer Zeit ausführbar
  • Er terminiert garantiert: d.h. ist nach endlich vielen Schritten fertig abgearbeitet, liefert ein Ergebnis und „hält an“
Definition
Algorithmus
  • Ein Algorithmus ist ein generelles, schrittweises, präzises, allgemeingültiges, endliches Lösungsverfahren für eine bestimmte Aufgabenart.
  • Er beruht auf elementaren Verarbeitungsschritten.
  • Alle Aufgaben einer bestimmten Art sind prinzipiell lösbar.

 

Stefan Schneider Wed, 08/21/2013 - 16:36
  • 7809 views

Beispiel

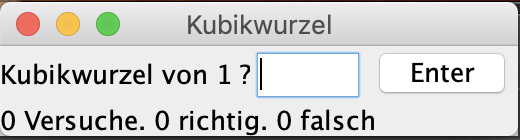
Beispiel

Das Problem des Findens einer Kubikwurzel ist ein Beispiel für das Entwickeln einer Lösungsidee und der Entwicklung eines Algorithmus.

Die Anwendung ist relativ klein und wahrscheinlich in der oberen linke Ecke des Bildschirms zu finden:

Screenshot der Kubikwurzelanwendung

Herunterladen der jar Datei mit Demoprogramm.

Starten:

  • Ihr JRE ist korrekt konfiguriert: Doppelklick auf der Datei Kubikwurzel.jar in Ihrem Download Ordner
  • oder: starten im Kommandozeilenfenster im Download Ordner mit dem Befehl java -jar Kubikwurzel.jar

Quellcode der Anwendung auf Github.

Problem

Bestimmen von Kubikwurzeln deren Ergebnis eine ganze Zahl zwischen Null und Hundert ist.

Das Demoprogramm links erlaubt Ihnen Ihre Fähigkeiten zu testen.

 

 

Stefan Schneider Fri, 08/23/2013 - 09:43
  • 5216 views

Lösungsidee

Lösungsidee

Lösungsidee 1: "Educated Guess"

Man kennt ja so einige Kubikwurzeln...

  • Kubikwurzel von 1 : 1
  • Kubikwurzel von 8 : 2
  • Kubikwurzel von 27 : 3
  • Kubikwurzel von 64 : 4
  • Kubikwurzel von 125 : 5
  • Kubikwurzel von 1000: 10

Lösungsidee 2: Taschenrechner mit Möglichkeit zur dritten Wurzel ziehen benutzen

Zum Kopfrechnen wenig geeignet...

Lösungsidee 3: Taschenrechner mit Potenzfunktion nutzen

Kubikwurzel x = x1/3

Zum Kopfrechnen auch weniger geeignet

Lösungsidee 4: Primzahlzerlegung!

8 = 2 * 2 * 2. Die Kubikwurzel von 8 ist 2!

Was tun bei größeren Zahlen?

Beispiel: 216 = 2 * 2 * 2 * 3 * 3 * 3

Lösung: 6 = 2 * 3

Vorgehen

Merke Dir jeden Primfaktor der dreimal vorkommt. Die Lösung ist das Produkt der Primfaktoren die 3 mal vorkommen.

Dieses Verfahren ist prinzipiell im Kopf zu meistern. Divisionen durch kleine Zahlen sind nicht so schwer.

Stefan Schneider Wed, 08/28/2013 - 13:50
  • 4720 views

Algorithmus

Algorithmus

Vorbedingung

Die vorgebene Zahl k soll eine Kubikwurzel aus den natürlichen Zahlen kleiner, gleich 100 besitzen

Der Algorithmus

Verbale Beschreibung UML Diagramm
  1. Merke Dir Ergebnis e mit dem Wert 1
  2. Bestimme einen Primfaktor f der Zahl k
  3. Multipliziere e mit f und merke das Ergebnis als e
  4. Teile die Zahl k dreimal durch den Primfaktor f.
  5. Merke dieses Ergebnis als k
  6. Wiederhole Algorithmus ab Schritt 2 wenn k größer als 1 ist.
  7. Die Lösung des Problems ist e
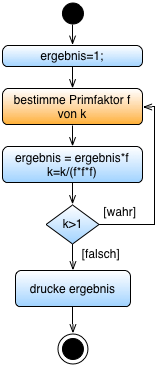 UML Flussdiagramm

 

Wir gehen davon aus, dass Merken, Dividieren, Multiplizieren elementare Anweisungen sind die nicht weiter verfeinert werden müssen.

Der Algorithmus wird immer terminieren, da die Division durch den letzten Primfaktor eins ergeben wird.

Das Teilproblem Primfaktor von k bestimmen ist aber kein elementares Problem. Zur Lösung dieses Teilproblems wird eine neue Lösungsidee und ein neuer Algorithmus benötigt.

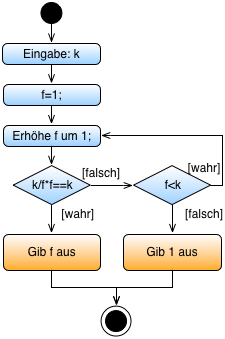
Teilalgorithmus Primfaktor einer Zahl k

Verbale Beschreibung UML Diagramm
  1. Setze f auf 1
  2. Erhöhe f um 1
  3. Ist k geteilt durch f (Ganzzahldivision) mal f = k ?
    1. Wenn ja: Gib f aus
    2. Wenn nein: Ist f kleiner als k ?
      1. Wenn ja: Springe zurück zum Erhöhen
      2. Wenn nein: Gib 1 aus (kein "echter" Primfaktor gefunden

Wie kann man diesen Algorithmus schneller machen?

 

Flussdiagramm Primfaktor
Stefan Schneider Wed, 08/28/2013 - 14:23
  • 4045 views

Implementierung in Java

Implementierung in Java

 Implementierung in Java

/**
* Berechnet die Kubikwurzel einer positiven Zahl
*
* @param k Zahl von der die Kubikwurzel berechnet werden soll.
* @return Ergebnis die Kubikwurzel
*/

public static int kubikwurzelVon(int k) {
   int ergebnis=1;
   do {
      int f = primfaktor(k);
      ergebnis = ergebnis*f;
      k = k / (f*f*f);
   } while (k>1);
   return ergebnis;
}

/**
* Diese Methode berechnet einen Primfaktor des Werts k
* Es wird 1 zurückgegeben wenn es keine anderen Primfaktoren
* gibt
* @param k Die Zahl von der ein Primfaktor berechnet wird
* @return f ein Primfaktor der Zahl oder 1 falls keiner existiert
*/
public static int primfaktor(int k) {
   int f = 1;
   do { 
      f++;
   } while ((k/f*f!=k)&&(f<k));
 
   if (f==k) f=1;
   return f;
}

Der Algorithmus zum Bestimmen eines Primfaktors ist sehr naiv...

Stefan Schneider Fri, 09/06/2013 - 09:29
  • 4408 views