Fragen zu Datenstrukturen
Fragen zu Datenstrukturen javafrage Wed, 03/22/2017 - 20:18- 2385 views
1 Binärbäume
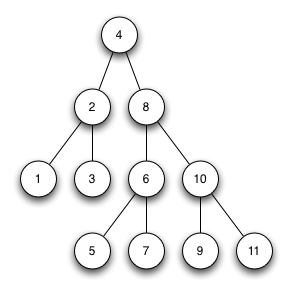
1 BinärbäumeWelche der Bäume sind korrekte, streng aufsteigend sortierte Binärbäume? Was sind die Fehler in den nicht korrekten Bäumen?
Geben Sie eine kurze Begründung.
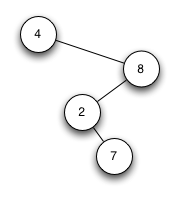
| Binärbaum 1 | Binärbaum 2 |
|---|---|
 |
 |
Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 4 Minuten |
- 4433 views
2 AVL-Bäume
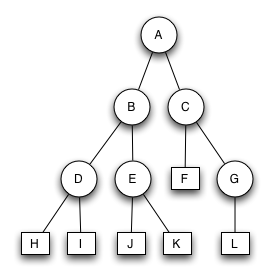
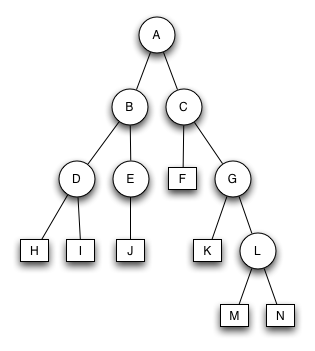
2 AVL-BäumeWelche der beiden Bäume sind korrekte AVL-Bäume? Was sind die Fehler in den nicht korrekten Bäumen?
| AVL-Baum 1 | AVL-Baum 2 |
|---|---|
 |
 |
Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 4 Minuten |
Antwort zu Frage 1: Binärbäume
Geben Sie eine kurze Begründung.
| Binärbaum 1 | Binärbaum 2 |
|---|---|
|
Dieser Baum ist korrket |
Dieser Baum ist nicht korrekt. Der Knoten 2 müsste links von 4 eingeordnet sein |
- 4362 views
3 Bruderbäume
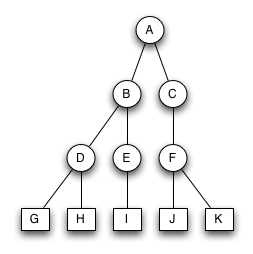
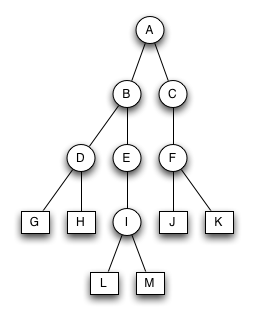
3 BruderbäumeWelche der beiden Bäume sind korrekte Bruderbäume? Was sind die Fehler in den nicht korrekten Bäumen? Bitte geben Sie eine kurze Erklärung.
| Bruder-Baum 1 | Bruder-Baum 2 |
|---|---|
 |
 |
Die Antwort finden Sie auf der nächsten Seite (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 4 Minuten |
Antwort zu Frage 2: AVL-Bäume
| AVL-Baum 1 | AVL-Baum 2 |
|---|---|
|
Der Baum ist ein korrekter AVL-Baum. |
Der AVL-Baum ist inkorrekt. Der Knoten F hat Höhe 3. Die Knoten M,N haben die Höhe 5. Bei AVL Bäumen ist nur ein Höhenunterschied von +/-1 erlaubt. |
- 4360 views
4 Erweitern eines AVL-Baums
4 Erweitern eines AVL-BaumsDer unten gezeigte Baum ist ein streng aufsteigend, sortierter Binärbaum und gleichzeitig ein AVL-Baum. Die Schlüssel in den Knoten sind ganze, positive Zahlen.
Fügen Sie 6 Knoten in das Diagramm ein.
- Wählen Sie die Knotenpositionen so, dass der Baum ein AVL-Baum bleibt.
- Tragen Sie dann die Schlüsselwerte so ein, dass der Baum streng sortiert bleibt.
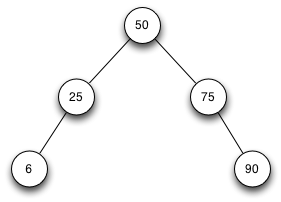
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 6 Minuten |
Antwort zu Frage 3: Bruderbäume
| Brudebaum 1 | Bruderbaum 2 |
|---|---|
|
Der Baum ist ein korrekter Bruderbaum |
Der Baum ist kein korrekter Bruderbaum. Die Knoten L und M haben eine andere Höhe. |
- 4230 views
Antwort auf Frage 3
Hallo, der rechte Baum wäre doch auch kein Bruderbaum wenn er zwar höhenbalanciert wäre aber nicht alle Söhne die gleiche Höhe hätten. Also der entscheidende Punkt ist ja nicht die Ausgeglichenheit sondern die Höhe der Söhne, oder?
Beste Grüße
- Log in to post comments
5 Definition von Brüdern (bei Brüderbäumen)
5 Definition von Brüdern (bei Brüderbäumen)Was sind Brüder im Kontext von Brüderbäumen?
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 2 Minuten |
Antwort zu Frage 4: Erweitern eines AVL-Baums
Eine mögliche Lösung
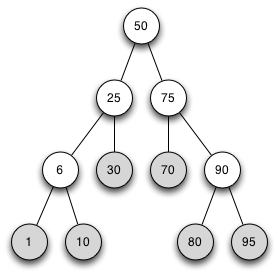
- 3761 views
6 Binär- und Bruderbäume
6 Binär- und BruderbäumeWann ist ein Binärbaum ein Bruderbaum? Nennen Sie die Kriterien.
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 6 Minuten |
Antwort zu Frage 5: Definition Bruder (bei Bruderbäumen)
Knoten die den gleichen Vater besitzen.
- 3764 views
7 Aufwände von Operationen in Listen, Warteschlangen und Bäumen
7 Aufwände von Operationen in Listen, Warteschlangen und BäumenWelche Aufwände O(n) haben die folgenden Operationen bei nicht optimierten Implementierungen?
- Einfügen eines Elements am Kopf einer Liste
- Suchen eines Elements in einer Liste
- Finden eines Elements in einem balancierten Baum
- Finden eines Elements in einem Feld(Array) bei bekanntem Index
- Finden eines Elements in einem Feld(Array) wenn der Zugriffsindex nicht bekannt ist
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 5 Minuten |
Antwort zu Frage 6: Binär- und Bruderbäume
- Jeder innere Knoten hat einen oder zwei Söhne
- Jeder unäre Knoten hat einen binären Bruderknoten
- Alle Söhne haben die gleiche Tiefe
- 4094 views
Alle Blattknoten haben die gleiche Tiefe
Vielen Dank für die Javafragen!
Sollte der letzte Stichpunkt der Antwort zu Frage 6 und 8 nicht heißen:
- Alle Blattknoten haben die gleiche Tiefe
Bei Fragen 8 und 9 ist mir außerdem aufgefallen, dass die Kommentarfunktion deaktiviert ist.
- Log in to post comments
Hallo,
habe die Kommentarfunktion wieder eingeschaltet. Das gab es mal böse Robots...
Zu den Söhnen. Das passt schon. Jeder Vater hat Söhne mit der gleichen Tiefe. Es können nicht alle Blattknoten im Baum die gleiche Höhe haben. Ein Vater ist immer um eins höher als sein Sohn.
- Log in to post comments
8 Definition Bruderbaum
8 Definition BruderbaumWelche drei Bedingungen gelten für einen Bruderbaum?
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 6 Minuten |
Antwort zu Frage 7: Aufwände von Operationen in Listen, Warteschlangen und Bäumen
- Einfügen eines Elements am Kopf einer Liste: O(1)
- Suchen eines Elements in einer Liste: O(n)
- Finden eines Elements in einem balancierten Baum: O(logN)
- Finden eines Elements in einem Feld(Array) bei bekanntem Index: O(1)
- Finden eines Elements in einem Feld(Array) wenn der Zugriffsindex nicht bekannt ist: O(n)
- 4440 views
9 Anforderungen an einen AVL-Baum
9 Anforderungen an einen AVL-BaumWas gilt für alle Teilbäume eines AVL-Baums?
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 2 Minuten |
Antwort zu Frage 8: Definition Bruderbaum
- Jeder innere Knoten hat einen oder zwei Söhne
- Jeder unäre Knoten hat einen binären Bruderknoten
- Alle Söhne eines Vaters haben die gleiche Tiefe
- 4054 views
Antwort zu Frage 8
Es sollte bei 3. m.E. heißen: Alle Blätter haben die gleiche Tiefe.
Denn, auch innere Knoten sind Söhne, haben jedoch unterschiedliche Tiefen.
Eine etwaige Änderung müsste auch im Artikel "Bruderbäume" übernommen werden.
- Log in to post comments
10 Bruderbaum korrigieren
10 Bruderbaum korrigieren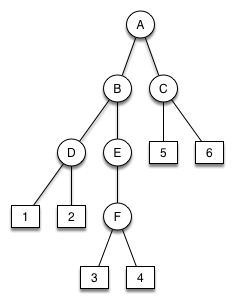 |
Der Baum links, ist mit seinen äusseren Blattknoten (Werte 1 bis 6) streng aufsteigend sortiert. Warum ist dieser Baum kein Bruderbaum? Geben Sie eine kurze Erklärung. Zeichnen Sie rechts einen Baum, der ein streng aufsteigend sortierter Bruderbaum ist. Er soll die gleichen 6 äusseren Blattknoten (Wert 1 bis 6) besitzen. |
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 6 Minuten |
Antwort zu Frage 9: Anforderungen an einen AVL-Baum
Die Höhe des linken Unterbaums unterscheidet sich um maximal 1 von der Höhe des rechten Unterbaums.
- 2512 views
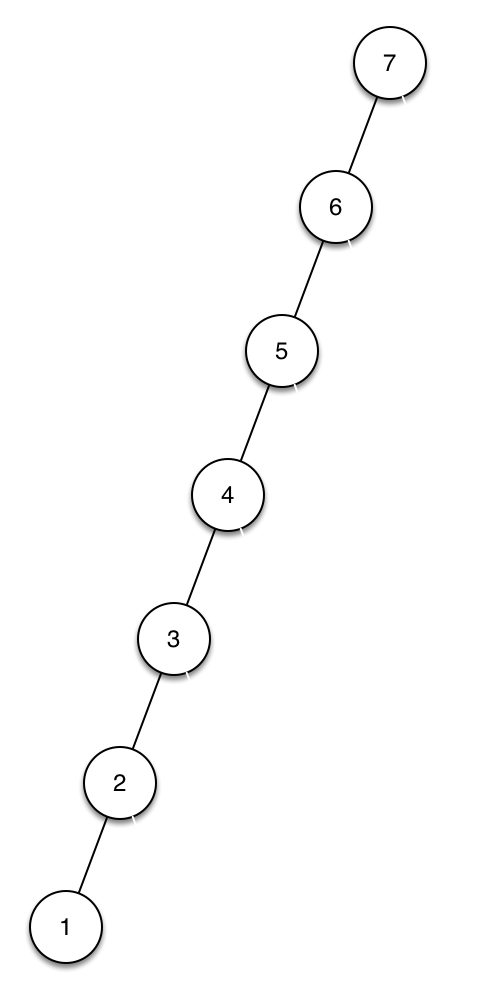
11 Höhenbalancierter Binärbaum
11 Höhenbalancierter Binärbaum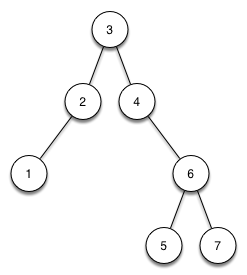 |
Der links gezeigte Binärbaum ist streng aufsteigend sortiert. Er ist nicht höhenbalanciert. Transformieren Sie die Knoten dieses Baums so, dass ein höhenbalancierter, streng sortierter Binärbaum der entsteht. |
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 5 Minuten |
Antwort zu Frage 10: Bruderbaum korrigieren
| Aufgabe | Lösung |
|---|---|
 |
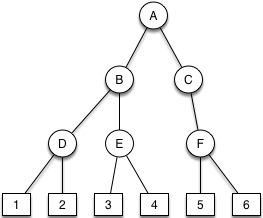 |
- 2976 views
Naja, schon irgendwie
andererseits: Es ist ein korrekter Bruderbaum. (Siehe Definition)
. Wer diese Aufgabe lösen kann, kennt die Definition...
- Log in to post comments
12 AVL Baum: Fehler erkennen und korrigieren
12 AVL Baum: Fehler erkennen und korrigieren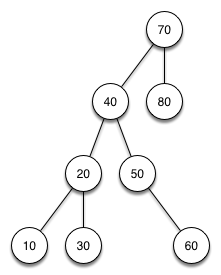 |
Der links gezeigte streng sortierte Binärbaum ist kein AVL Baum. Warum ist er kein AVL Baum? Geben Sie eine kurze Begründung:
Zeichnen Sie rechts die gleichen Knoten als einen streng aufsteigend, sortierten AVL-Baum ein: |
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 2+4 Minuten |
Antwort zu Frage 11: Höhenbalancierter Binärtbaum
| Aufgabe | Lösung |
|---|---|
 |
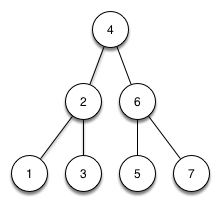 |
- 2696 views
13 Warteschlangen
13 WarteschlangenDie „einfache“ Warteschlange wird in echten Implementierungen eher selten eingesetzt. Nennen Sie den wichtigsten Nachteil einer „einfachen“ Warteschlange. Welcher Warteschlangentyp wird in realen Implementierungen eher eingesetzt. Nennen Sie den Fachbegriff. Was ist der Vorteil dieses Warteschlangentyps?
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 2+2 Minuten |
Antwort zu Frage 12: AVL Baum: Fehler erkennen und korrigieren
Knoten „80“ hat keinen Unterbaum (Höhe 1). Der Unterbaum von „40“ rechts hat die Höhe 3. Die Unterbäume dürfen sich in der Höhe nur um 1 unterscheiden.
| Aufgabe | Lösung |
|---|---|
 |
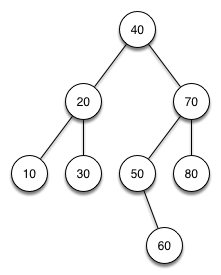 |
- 2958 views
Alternative Lösung
Könnte man nicht auch einfach die 60 links unter die 80 schreiben? Dann müsste man nicht den ganzen Baum ändern
- Log in to post comments
14 Streng sortierte Binärbäume
14 Streng sortierte BinärbäumeNennen Sie drei Eigenschaften die für jeden inneren Knoten eines streng
aufsteigend sortierten Binärbaums gelten.
Die Antwort finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 3 Minuten |
Antwort zu Frage 13: Warteschlangen
Einfache Warteschlangen können beliebig groß werden falls ein Prozessor, der die Warteschlange bedient ausfällt. Dieser Ausfalls des Prozessors der die Warteschlange abarbeitet und Elemente löscht wird dann zu einem Hauptspeicheproblem führen. Das Hauptspeicherproblem kann dann die gesamte Anwendung stoppen.
Die Lösung:
Ringsspeicher auch Ringpuffer genannt.
Sie haben einen konstanten Speicherverbrauch.
- 1872 views
15 Maximaler Aufwand für Binärbaum
15 Maximaler Aufwand für Binärbaum| Der streng sortierte Binärbaum (rechts) gewährleistet einen Zugriff auf alle Knoten mit einem minimalen Aufwand. Zeichnen Sie rechts daneben einen streng sortierten Binärbaum mit den gleichen Werten der den höchstmöglichen (schlechtesten) Aufwand für den Zugriff auf alle Knoten besitzt | 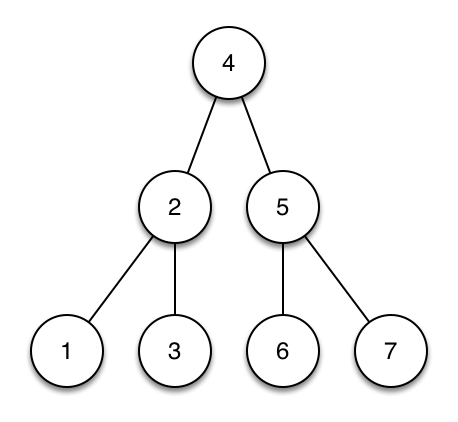 |
Die Antwort finden Sie unten auf dieser Seite.
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 4 Minuten |
Antwort zu Frage 14: Streng sortierte Binärbäume
- Jeder Knoten hat einen oder zwei Söhne
- Jeder linke Sohn ist kleiner als der Vater
- Jeder rechte Sohn ist größer als der Vater
Antwort zu Frage 15: Maximaler Aufwand für Binärbaum
|
Ein Baum der zu einer Liste degeniert ist hat den schlechtesten Aufwand O(n). Anbei ein Beispiel: |
|
- 2024 views