4 Heapsort, Baumpräsentation, Heapbedingung
4 Heapsort, Baumpräsentation, HeapbedingungZeigen Sie wie der logische Baum eines Heapsorts für ein gegebenes Feld von Schlüsseln aussieht.
Tragen Sie die Schlüssel und den Feldindex (die Feldposition) der Feldrepräsentation in die Heappräsentation unten ein.
Im Beispiel unten ist auf der Position 1 der Schlüssel 9 zu finden.
Tragen Sie Positionen und Schlüssel in das vorgegebene Baumdiagramm ein:
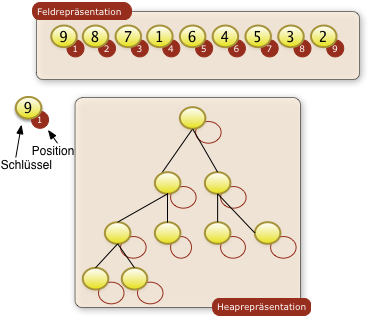
Gilt die Heapbedingung für diese Folge? Markieren Sie Knoten die die Heapbedingung verletzen.
Die Antworten finden Sie hinter der nächsten Frage (URL rechts unten klicken).
| Niveau | 2 |
| Schwierigkeitsgrad | mittel |
| Zeit | 5+2 Minuten |
Antwort zu Frage 3: Ungünstige Zahlenreihen für den Quicksort
Weil keine ähnlich großen Teilintervalle entstehen.
Im schlimmsten Fall wird das Teilintervall immer nur um ein Element verkleinert.
Der Aufwand ist dann (n-1)+O(n-2)+...+O(3)+O(2)=O(n2) (Arithmetische Reihe)
Der Aufwand zum Bearbeiten der Teilintervalle kann dann im schlimmsten Fall O(n2) anstatt O (n*log(n)) wie bei ähnlich großen Teilintervallen sein.
- 4517 views