Algorithmen
AlgorithmenZeitkomplexität von Algorithmen
Ziel ist immer die effiziente Ausführung von Algorithmen in einer minimalen Zeit, mit einem minimalen Aufwand (Ausführungsaufwand).
Der Ausführungsaufwand ist zu unterscheiden vom Aufwand den Algorithmus zu entwickeln, dem Entwicklungsaufwand. Langsame Anwendungen sind leider oft das Resultat von Implementierungen bei denen die Kostengründe für den Entwicklungsaufwand zu einem höheren Ausführungsaufwand führen...

Der Ausführungsaufwand hängt von vielen Faktoren ab. Viele Faktoren beruhen auf den unbekannten Komponenten des Ausführungssystems:
- Betriebssystem
- Prozessor, Prozessorgeschwindigkeit
- Hauptspeichergröße und - geschwindigkeit
- etc.
Die verlässlichste Art und Weise zur Beurteilung der Zeiteffizienz von Algorithmen ist die Abschätzung der Anzahl der Verarbeitungsschritte in Abhängigkeit von der Anzahl der Daten die zu verarbeiten sind.
| Ordnung "O" eines Algorithmus |
|---|
| Die funktionale Abhängigkeit (bzw. Proportionalität) zwischen der Zahl der Ausführungsprogrammschritte und der Zahl (n) der zu verarbeitenden Datenelemente |
Beispiele
- O(n): Ein Algorithmus hat eine lineare, proportionale Abhängigkeit von der Anzahl der Elemente. Verdoppelt sich die Anzahl der Elemente, so verdoppelt sich auch die Anzahl der Ausführungsschritte und damit die Ausführungsdauer
- O(n2): Die Anzahl der Ausführungsschritte steigt mit dem Quadrat der zu behandelten Element. Der Ausführungsaufwand vervierfacht sich bei der Verdopplung der Ausführungsschritte.
- O(log n): Die Anzahl der Ausführungsschritte steigt mit dem Logarithmus der Anzahl der Elemente
Hierdurch ergeben sich verschiedene Kategorien von Problemen:
Praktisch ausführbare Algorithmen
|
Algorithmen die auch bei einer sehr viel größeren Zahl von Elementen in einer akzeptablen Zeit ausgeführt werden können. Dies sind im Idealfall: O(n), O(log n), O (n*log n) Man zählt hierzu aber auch Algorithmen mit einer polynomialen Ordnung wie O(n2) oder O(n3). |
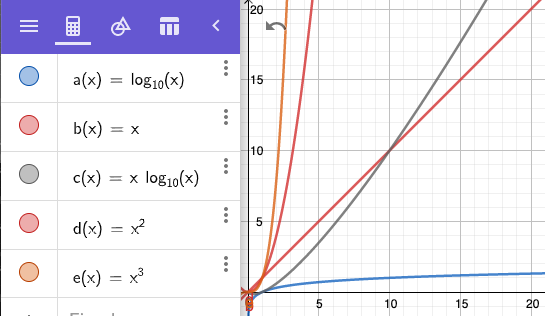 |
Praktisch nicht mehr ausführbare Algorithmen
Praktisch nicht mehr ausführbare Algorithmen lassen sich nicht in akzeptabler Zeit bei größer werdenden Datenbeständen ausführen. Dies sind Algorithmen mit einer exponentiellen Ordnung. O(xn). Hierzu zählt auch das Problem des Handlungsreisenden mit einer Ordnung von O(n!).
- 7283 views
Rechenregeln für die Aufwandsbestimmung
Rechenregeln für die AufwandsbestimmungDie Rechenregeln für die Aufwände von Algorithmen erlauben dem Entwickler die Komplexitätsklasse eine Algorithmus abzuschätzen.
Hierzu muß der Entwickler zuerst bestimmen von welchem Parameter die Ausführungszeit primär abhängt.
 |
Ein Beispiel: Konvertierung von Bildern Der Algorithmus soll eine Anzahl von n Bildern mit einer mittleren Größe vom m Byte konvertieren.
Sehr wahrscheinlich wird die Anzahl der Bilder n nach dem bekanntmachen des Dienstes sehr schnell steigen. Die Größe m von Bildern, ist aber in der Vergangenheit durch neue Technologien, auch gestiegen. Es kann also sein, daß sich die Kriterien mit der Zeit ändern! |
Hierzu geht der Entwickler in zwei Schritten vor:
- Man bestimmt die Anzahl der auszuführenden Befehle eines Algorithmus in Abhängigkeit von den zu verarbeitenden Datenelementen n
- Man vereinfacht den Term mit dem Gesamtaufwand derart, dass der Term und jeder Teilterm in der gleichen Komplexitätsklasse bleibt
Am Ende bleibt dann ein einfacher Ausdruck für die Komplexitätsklasse übrig.
Klassen von Komplexität
- konstant: O(1)
- logarithmisch: O(log(n))
- linear: O(n)
- jenseits von linear: O(n*log(n))
- polynomial: O(n2), O(n3), O(n4) etc.
- exponentiell: O(kn)
Rechenregeln für einfache Betrachtungen
Gegeben sei eine Funktion f(n) mit dem Aufwand O(n). n sei die variable Anzahl der zu verarbeitenden Datenelemente
- Konstanten: Konstanten haben keinen Einfluss:
- O(f(n)+k) = O(f(n))+k = O(f(n)) für k konstant
- O(f(n)*k)=O(f(n))*k = O(f(n)) für k konstant
- O(k) = O(1)
- konstante Aufwände werden nicht einberechnet. Dies gilt für Multiplikation, sowie für die Addition.
- Nacheinander ausgeführte Funktion f und g
- Der Aufwand O(f(n)) sei größer als der Aufwand von O(g(n))
- O(f(n)+g(n))=O(f(n))+O(g(n)) = O(f(n))
- ... der größere Aufwand gewinnt.
- Ineinander geschachtelte Funktionen oder Programmteile wie Schleifen f(g(n))
- O(f(g(n))) = O(f(n))*O(g(n))
- der Aufwand multipliziert sich.
- Einschränkung: Hier wird davon ausgegangen, dass beide Schleifen von der gleichen Variablen abhängen!
Weitere Informationen
- bigocheatsheet.com: Know Thy Complexities!
- 5657 views
Vorbereitung Gruppenarbeit
Vorbereitung GruppenarbeitDie Vorlesung wird virtuell oder in einem Klassenraum gegeben. Sie müssen nichts vorbereiten fall die Vorlesung im Klassenraum gehalten wird, der Referent wird alles nötige zur Gruppenarbeit mitbringen!
Es wird eine Gruppenarbeit durchgeführt in der sich jede Gruppe einen Sortieralgorithmus erarbeitet und dem Kurs vorstellt. Hierzu ist es nützlich das Folgende zu haben:
1. Literatur
Das Skript ist hilfreich. Das Internet ist hilfreich. Ein Buch wie "Algorithmen und Datenstrukturen" von Ottmann und Wildmayer ist sehr hilfreich.
2. Didaktische Hilfsmittel
Sie werden den Algorithmus im Team diskutieren und Sie werden den Algorithmus im Kurs vorstellen müssen. Man benötigt etwas zum Sortieren was auf den Schreibtisch passt. Hier sind zwei "Lowtech" Optionen.
 |
Spielkarten: Sie haben eine Kardinalität (Ordnung). Sie müssen sortiert werden. Man kann Sie gut zeigen. Sie sind transportabel |
Noch besser sind Stifte!
und man hat meistens sowieso ein paar im Mäppchen... 😀 |
 |
Die genauen Anweisungen sind im Übungsteil des Skripts zu finden.
- 261 views
Suchalgorithmen
Suchalgorithmen |
Such- und Sortiervorgänge sind sehr häufige Aufgaben die in Anwendungen gelöst werden müssen. Suchen ist ein Vorgang der komplementär zum Sortieren ist. Datenbestände die vollständig oder teilweise sortiert sind, lassen sich wesentlich einfacher durchsuchen. Ungeordnete Datenbestände lassen sich lassen sich im schlechtesten Fall nur linear durchsuchen. Suchvorgänge lassen wie folgt kategorisieren:
|
Internes und externes Suchen
Man unterscheidet zwischen Suchvorgängen bei denen man den gesamten Datenbestand im Hauptspeicher verwalten kann (internes Suchen) und Suchvorgängen bei denen der Datenbestand nur teilweise in den Hauptspeicher geladen werden kann(externes Suchen).
Beim externen Suchen muss man also einen schnellen, aber begrenzten Hauptspeicher geschickt einsetzen um einen langsamen, aber kostengünstigeren Massenspeicher zu durchsuchen.
Die Unterscheidung zwischen den beiden Suchverfahren ist sehr wichtig für produktiv eingesetzte Anwendungen, in der Berechung der Zeitaufwände ist sie nicht hilfreich!
Ein Festplattenspeicher mag etwa 1000 mal langsamer als der Hauptspeicher eines Rechners sein. Dies macht bei einer echten Anwendung einen großen Unterschied. Bei der Berechnung der Zeitkomplexität wird dieser Faktor jedoch als "unbedeutend" weggekürzt.
Suchverfahren
- 7632 views
Sequentielle Suche (lineare Suche)
Sequentielle Suche (lineare Suche)Die sequentielle Suche beruht auf dem naiven Ansatz einen Datenbestand vollständig zu durchsuchen bis das passende Element gefunden wird. Dieses Verfahren nennt man auch erschöpfende Suche oder im englischen das Greedy-Schema (engl. für gefräßig). Der Algorithmus für das Durchsuchen eines Felds ist der folgende:
- Spezifiziere Suchschlüssel
- Vergleiche jedes Element mit dem Suchschlüssel
- Erfolgsfall: Liefere Indexposition beim ersten Auffinden des Objekts und beende das Suchen
- Kein Erfolg: Gehe zum nächsten Objekt und vergleiche es.
- Gib eine Meldung über das erfolglose Suchen zurück wenn das Ende des Datenbestands erreicht wurde, ohne daß, das Objekt gefunden wird. Dies kann eine java-Ausnahme sein oder ein spezieller Rückgabewert (z.Bsp .1)
Der Aufwand für diesen Algorithmus ist linear, also O(n). Die Anzahl der nötigen Vergleichsoperationen hängt direkt von der Anzahl der Elemente im Datenbestand ab. Im statischen Mittel sind dies n/2 Vergleiche.
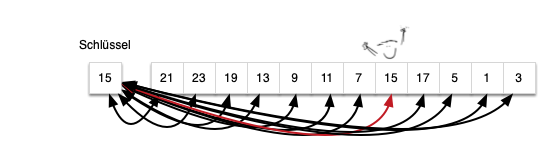
Sequentielle Suche in einem unsortierten Datenbestand
In diesem Fall muss bei jeder Suche der gesamte Datenbestand durchlaufen werden bis ein Element gefunden wurde
Beispiel einer Javaimplementierung
Die Methode sequentielleSuche() durchsucht ein Feld von 32 Bit Ganzzahlen nach einem vorgegebenen Schlüssel schluessel und gibt den Wert -1 zurück wenn kein Ergebnis gefunden wird.
public static int sequentielleSuche() (int[] feld, int schluessel) {
int suchIndex = 0;
while (suchIndex< feld.length && feld[suchIndex] != schluessel) suchIndex++;
if (suchIndex == feld.length) suchindex = -1; // Nichts gefunden
return suchindex;
}
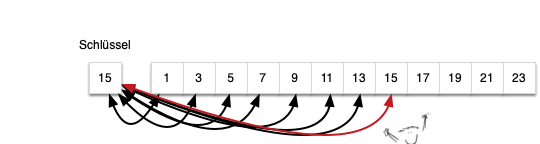
Sequentielle Suche in einem sortierten Datenbestand
Bei einem sortierten Datenbestand kann man die Suche optimieren in dem man sie abbricht so bald man weiß, das die folgenden Elemente alle größer bzw. kleiner als das gesucht Element sind. Man muss also nicht das Feld vollständig durchlaufen. Hierdurch lässt sich Zeit sparen. Der durchschnittliche Aufwand von n/2 bleibt jedoch ein linearer Aufwand.
Beispiel einer Javaimplementierung
Die Methode sequentielleSuche() durchsucht ein Feld von 32 Bit Ganzzahlen nach einem vorgegebenen Schlüssel schluessel und gibt den Wert -1 zurück wenn kein Ergebnis gefunden wird.
public static int sequentielleSuche() (int[] feld, int schluessel)
int suchIndex = 0;
while (suchIndex< feld.length && feld[suchIndex] < schluessel) suchIndex++;
if ((suchindex < feld.length) && (feld[suchIndex] == feld[schluessel]))
return suchindex; // Erfolg
else return -1; //kein Erfolg
}- 25830 views
Binäre Suche
Binäre SucheDie binäre Suche erfolgt nach dem "Teile und Herrsche" Prinzip (divide et impera) durch Teilen der zu durchsuchenden Liste.
Voraussetzung: Die Folge muss steigend oder fallend sortiert sein!
Der Algorithmus lässt sich sehr gut rekursiv beschreiben:
Suche in einer sortierten Liste L nach einem Schlüssel k:
- Beende die Suche erfolglos wenn die Liste leer ist
- Nimm das Element auf der mittleren Position m der Liste und Vergleiche es mit dem Schlüssel
- Falls der Schlüssel k kleiner als dasElement L[m] is (k<L[m]) durchsuche die linke Teilliste bis zum Element L[m]
- Falls der Schlüssel k größer als dasElement L[m] is (k>L[m]) durchsuche die rechte Teilliste vom Element L[m] bis zum Ende
- Beende die Suche wenn der Schlüssel k gleich L[m] ist (k=L[m])
Das binäre Suchen ist ein Standardverfahren der Informatik da es sehr effizient ist. Der Aufwand beträgt selbst im ungünstigsten Fall O(N)=log2(N).
Im günstigsten Fall ist der Aufwand O(N)=1 da eventuell der gesuchte Schlüssel sofort gefunden wird.
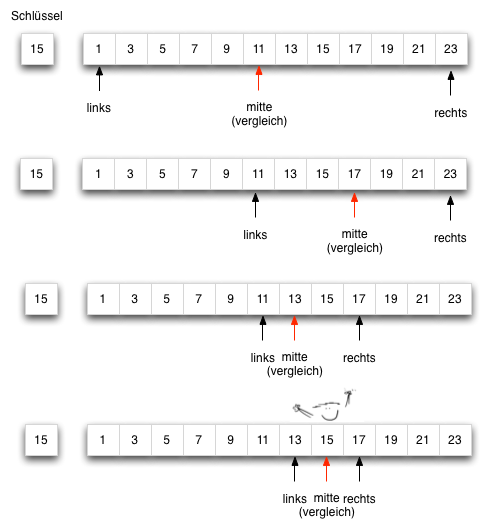
Beispiel einer binären Suche
Das folgende Feld hat 12 Elemente zwischen 1 und 23. Es wird ein Element mit dem Wert 15 gesucht. Zu Beginn ist das Suchintervall das gesamte Feld von Position 0 (links) bis 11 (rechts). Der Vergleichswert (mitte) wird aus dem arithmetischen Mittel der Intervallgrenzen berechnet.
Beispielimplementierung in Java
Die Methode binaerSuche() sucht einen Kandidaten in einem aufsteigend sortierten Feld von Ganzzahlen. Das Hauptprogramm erzeugt ein Feld mit der Größe 200 und aufsteigenden Werten
public class Binaersuche {
int[] feld;
/**
*
* @param feld: Das zu durchsuchende Feld
* @param links: linker Index des Intervalls
* @param rechts: rechter Index des Intervalls
* @param kandidat: der zu suchende Wert
*/static void binaerSuche(int[] feld, int links,int rechts, int kandidat) {
int mitte;
do{
System.out.println("Intervall [" + links +
"," + rechts + "]");
mitte = (rechts + links) / 2;
if(feld[mitte] < kandidat){
links = mitte + 1;
} else {
rechts = mitte - 1;
}
} while(feld[mitte] != kandidat && links <= rechts);
if(feld[mitte]== kandidat){
System.out.println("Position: " + mitte);
} else {
System.out.println("Wert nicht vorhanden!");
}
}
public static void main(String[] args) {
int groesse=200;
int[] feld = new int[groesse];
for (int i=0; i<feld.length;i++)
feld[i] = 2*i; //Feld besteht aus geraden Zahlen
System.out.println("Suche feld["+ 66 + "]=" + feld[66]);
binaerSuche(feld, 0,(feld.length-1), feld[66]);
}
}
Programmausgabe auf Konsole:
Suche feld[66]=132
Intervall [0,199]
Intervall [0,98]
Intervall [50,98]
Intervall [50,73]
Intervall [62,73]
Intervall [62,66]
Intervall [65,66]
Intervall [66,66]
Position: 66
Tipp: Nutzen Sie Arrays.binarySearch()
Die Systemklasse Arrays bietet nützliche Methoden zum Arbeiten mit Feldern an. Nutzen Sie die überladene, statische Methode Arrays.binarySearch() zum Suchen in einem Feld.
Das funktioniert natürlich nur in einem sortierten Feld. Dafür gibt es ja die überladene, statische Methode Arrays.sort()...
Ein Beispiel mit der main() Methode von oben:
public static void main(String[] args) {
int groesse=200;
int[] feld = new int[groesse];
for (int i=0; i<feld.length;i++)
feld[i] = 2*i; //Feld besteht aus geraden Zahlen
System.out.println("Suche feld["+ 66 + "]=" + feld[66]);
Arrays.sort(feld);
int ergebnis = Arrays.binarySearch(feld,feld[66]);
}
Weiterführende Quellen und Beispiele
- 39430 views
Wieso Feldgröße / 3
Wieso teile ich meine groesse = 200 durch 3 und nicht durch 2? der suchalgorithmus fängt doch in der Mitte an oder ist mit der ersten Ausgabe etwas anderes gemeint?
- Log in to post comments
Beispielanwendung zum Suchen
Beispielanwendung zum SuchenDas folgende Programm zeigt eine sequentielle und eine binäre Suche in einem Feld mit zufälligen Werten.
Die Variable groesse erlaubt es die Größe des Felds zu verändern. Mit dem Nanotimer werden die benötigten Zeiten gemessen. Vergleichen Sie die Zeitaufwände für das sequentielle und das binäre Suchen mit dem Zeitaufwand für das Sortieren mit der Hilfklasse Arrays!
package s2.sort;
import java.util.Arrays;
/**
*
* @author sschneid
* @version 1.0
*/
public class Suchen {
public static int[] feld;
public static int groesse = 10000000;
/**
* Hauptprogramm
* @param args
*/
public static void main(String[] args) {
erzeugeFeld();
int suchwert =feld[groesse-2];
System.out.println("Suche feld["+ (groesse-2) +"] = " + suchwert);
sucheSequentiell(suchwert);
sortiere();
binaereSucheSelbst(suchwert);
binaereSuche(suchwert);}
/**
* Erzeuge ein Feld mit Zufallszahlen
*/
public static void erzeugeFeld() {
feld = new int[groesse];
for (int i=0; i<feld.length;i++) {
feld[i]=(int)(Math.random() * (double)Integer.MAX_VALUE);
}
System.out.println("Feld mit "+ groesse + " Elementen erzeugt.");
}
/**
* Suche sequentiell einen Wert in einem unsortierten Feld
* @param suchwert der gesuchte Wert
*/
public static void sucheSequentiell(int suchwert) {
System.out.println("Sequentielle Suche nach Schlüssel");
long t = System.nanoTime();
int i=0;
while ( (i<groesse) && (suchwert != feld[i])) i++;
t = (System.nanoTime() -t)/1000000;
if (i== groesse) {
System.out.println(" Der Wert: " + suchwert +
" wurde nicht gefunden");
}
else {
System.out.println(" Der Suchwert wurde auf Position " + i +
" gefunden");
}
System.out.println(" Dauer sequentielle Suche: " + t +"ms");
}
/**
* Sortiere ein Feld mit der Klasse Arrays und messe die Zeit
* @param suchwert der gesuchte Wert
*/
public static void sortiere() {
System.out.println("Sortieren mit Arrays.sort()");
long t = System.nanoTime();
Arrays.sort(feld);
t = (System.nanoTime() -t)/1000000;
System.out.println(" Feld sortiert in " + t +" ms");
}
/**
* Suche binär einen Wert in einem sortierten Feld
* @param suchwert der gesuchte Wert
*/
public static void binaereSucheSelbst(int suchwert) {
System.out.println("Selbstimplementierte binäre Suche");
long t = System.nanoTime();
int intervall = (feld.length+1)/2;
int pos = intervall;
while ((intervall > 1) && (feld[pos] != suchwert)) {
intervall =(intervall+1)/2;
if ((feld[pos] > suchwert)) {pos -= intervall;}
else {pos += intervall;}
}
t = (System.nanoTime() -t);
if (feld[pos]== suchwert) {
System.out.println(" Der Suchwert wurde auf Position " +
pos +" gefunden");
}
else {
System.out.println(" Der Wert: " + suchwert +
" wurde nicht gefunden");
}
System.out.println(" Dauer binäre Suche " + (t/1000000) +"ms" +
" (" + t + " ns)");
}
/**
* Suche binär einen Wert in einem sortierten Feld
* Nutze die binäre Suchmethode der Klasse Arrays
* @param suchwert der gesuchte Wert
*/
public static void binaereSuche(int suchwert) {
System.out.println("Binäre Suche mit Arrays.binarySearch()");
long t = System.nanoTime();
int pos = Arrays.binarySearch(feld, suchwert);
t = (System.nanoTime() -t);
System.out.println(" Der Suchwert wurde auf Position " +
pos +" gefunden");
System.out.println(" Dauer binäre Suche " + (t/1000000) +
"ms" + " (" + t + " ns)");
}}
Klasse in github.
Typische Konsolenausgabe:
Feld mit 10000000 Elementen erzeugt.
Suche feld[9999998] = 1719676120
Sequentielle Suche nach Schlüssel
Der Suchwert wurde auf Position 9999998 gefunden
Dauer sequentielle Suche: 28ms
Sortieren mit Arrays.sort()
Feld sortiert in 1296 ms
Selbstimplementierte binäre Suche
Der Suchwert wurde auf Position 8008593 gefunden
Dauer binäre Suche 0ms (6000 ns)
Binäre Suche mit Arrays.binarySearch()
Der Suchwert wurde auf Position 8008593 gefunden
Dauer binäre Suche 0ms (11000 ns)
- 8121 views
Sortieralgorithmen
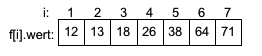
SortieralgorithmenIn diesem Abschnitt gehen wir davon aus, dass die zu sortierenden Datensätze in einem Feld f der Größe N in aufsteigender Reihenfolge sortiert werden. Die Feldelemente sollen in aufsteigender Reihenfolge sortiert werden.
Das Feld f dient als Eingabe für die Folge des Sortierverfahrens sowie als Ausgabedatenstruktur. Die Elemente müssen also innerhalb des Folge umsortiert werden. Nach dem Sortieren gilt für das Feld f:
f[1].wert <= f[2].wert ...<=f[N].wert
Beispiel
|
Unsortierte Folge mit N=7 Elementen:
|
Sortierte Folge mit N=7 Elementen
|
Bewertungskriterien
Bei der Bewertung der der Sortieralgorithmen wird jeweils in Abhängigkeit der Größe des zu sortierenden Feldes
- die Anzahl der Schlüsselvergleiche C (englisch comparisons) und
- die Anzahl der Bewegungen M (englisch: movements) der Elemente
gemessen.
Bei diesen zwei Parametern interessieren
- der beste Fall (die wenigsten Operationen)
- der schlechteste Fall (die meisten Operationen)
- der durchschnittliche Fall
Schlüsselvergleiche sowie Bewegungen tragen beide zur Gesamtlaufzeit bei. Man wählt den größeren der beiden Werte um eine Abschätzung für die Gesamtlaufzeit zu erlangen.
Stabilität von Sortierverfahren
Ein weiteres Kriterium für die Bewertung von Sortiervorgängen ist die Stabilität.
| Definition: Stabiles Sortierverfahren |
|---|
| Ein Sortierverfahren ist stabil wenn nach dem Sortieren die relative Ordnung von Datensätzen mit dem gleichen Sortierschlüssel erhalten bleibt. |
Beispiel: Eine Folge von Personen die ursprünglich nach der Mitarbeiternummer (id) sortiert. Diese Folge soll mit dem Nachnamen als Sortierschlüssel sortiert werden.
Im folgenden Beispiel wurde ein stabiles Sortierverfahren angewendet. Die relative Ordnung der beiden Personen mit dem Namen "Schmidt" bleibt erhalten. Der Mitarbeiter mit der Nummer 18 bleibt vor dem Mitarbeiter mit der Nummer 21.
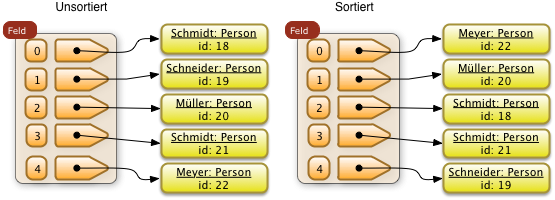
Bei nicht stabilen Sortierverfahren bleibt diese relative Ordnung nicht unbedingt erhalten. Hier könnte eine sortierte Folge so aussehen:
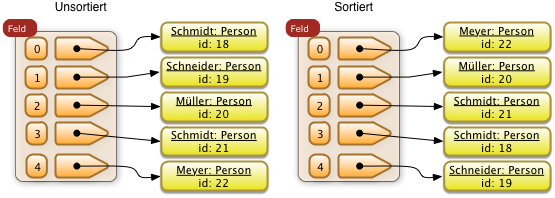
Stabile Sortierverfahren erlauben das Sortieren nach mehreren Prioritäten da eine Vorsortierung erhalten wird.
Im oben gezeigten Beispiel kann man eine Folge
- primär nach Nachnamen sortierten und
- sekundär nach der Personalnummer (id).
Man sortiert die Personen zuerst nach dem Kriterium mit der niedrigen Priorität. Dies ist hier die Personalnummer. Diese Vorsortierung war schon gegeben. Anschließend sortiert man nach dem wichtigeren Kriterium, dem Nachnamen. Die so entstandene Folge ist primär nach Nachnamen sortieret, sekundär nach Personalnummer.
- 17855 views
Beispielprogramme
BeispielprogrammeDie folgenden Beispielprogramme erlauben das Testen von unterschiedlichen Sortieralgorithmen.
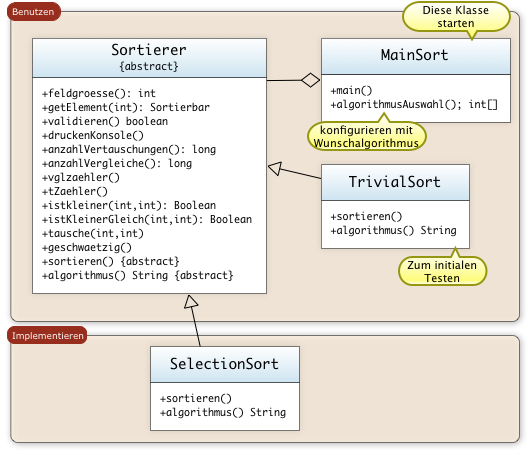
Hinweis: Die Implementierungen der Sortieralgorithmen selbst sind in den Abschnitten der Algorithmen zu finden. Im Hauptprogramm MainSort kann man durch Instanziieren einen Sortieralgorithmus wählen.
Arbeitsanweisung
Kopieren, Bauen und Starten der Referenzimplementierung
- Legen Sie in Ihrer Entwicklungsumgebung das Paket s2.sort an
- Kopieren Sie die Quellen der unten aufgeführten Klassen (inklusive Trivialsort) in Ihre Entwicklungsumgebung. Achten Sie darauf, daß alle Klassen im Paket s2.sort angelegt werden.
- Übersetzen Sie alle Klassen
- Starten Sie Anwendung durch Aufruf der Klasse s2.sort.MainSort
Auf der Kommandozeile geschieht das mit dem Befehl
$ java s2.sort.MainSort
Die Konsolenausgabe dieser Anwendung ist:
Phase 1: Einfacher Test mit 6 Elementen Algorithmus: Sortiere drei Werte Unsortiert: feld[0]=6 feld[1]=2 feld[2]=4 feld[3]=3 feld[4]=5 feld[5]=7 Zeit(ms): 0 Vergleiche: 2 Vertauschungen: 2. Fehler in Sortierung Sortiert: feld[0]=2 feld[1]=4 feld[2]=6 feld[3]=3 feld[4]=5 feld[5]=7 Keine Phase 2 (Stresstest) aufgrund von Fehlern...
Der Trivialsort hat leider nur die Schlüssel auf der Position 0 und 1 sortiert.
Effizienz des Algorithmus messen
Das Hauptprogramm MainSort wird bei einer korrekten Sortierung eines Testfelds mit 6 Werten automatisch in die zweite Phase eintreten.
Hier wird es ein Feld mit 5 Werten und Zufallsbelegungen Generieren und Sortieren.
Die Feldgröße wird dann automatisch verdoppelt und es wird eine neue Sortierung mit neuen Zufallswerten durchgeführt. Dies wird solange wiederholt bis ein Sortiervorgang eine voreingestellte Maximalzeit (3 Sekunden) überschritten hat.
Mit Hilfe dieser Variante kann man die benötigte Zeit pro Anzahl sortierter Elemente beobachten und die Effizienz des gewählten Algorithmus abschätzen.
Beim Sortieren durch Auswahl ergibt die die folgende Konsolenausgabe:
Phase 1: Einfacher Test mit 6 Elementen Algorithmus: Sortieren durch Auswahl Unsortiert: feld[0]=6 feld[1]=2 feld[2]=4 feld[3]=3 feld[4]=5 feld[5]=7 Zeit(ms): 0 Vergleiche: 15 Vertauschungen: 5. Korrekt sortiert Sortiert: feld[0]=2 feld[1]=3 feld[2]=4 feld[3]=5 feld[4]=6 feld[5]=7 Phase 2: Stresstest Der Stresstest wird beendet nachdem mehr als 3 Sekunden benötigt werden. Maximalzeit(s): 3 Sortieren durch Auswahl. Feldgroesse: 10 Zeit(ms): 0 Vergleiche: 45 Vertauschungen: 9. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 20 Zeit(ms): 0 Vergleiche: 190 Vertauschungen: 19. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 40 Zeit(ms): 0 Vergleiche: 780 Vertauschungen: 39. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 80 Zeit(ms): 1 Vergleiche: 3160 Vertauschungen: 79. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 160 Zeit(ms): 5 Vergleiche: 12720 Vertauschungen: 159. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 320 Zeit(ms): 14 Vergleiche: 51040 Vertauschungen: 319. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 640 Zeit(ms): 14 Vergleiche: 204480 Vertauschungen: 639. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 1280 Zeit(ms): 19 Vergleiche: 818560 Vertauschungen: 1279. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 2560 Zeit(ms): 26 Vergleiche: 3275520 Vertauschungen: 2559. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 5120 Zeit(ms): 84 Vergleiche: 13104640 Vertauschungen: 5119. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 10240 Zeit(ms): 575 Vergleiche: 52423680 Vertauschungen: 10239. Korrekt sortiert Sortieren durch Auswahl. Feldgroesse: 20480 Zeit(ms): 1814 Vergleiche: 209704960 Vertauschungen: 20479. Korrekt sortiert
Warnung
- Diese zweite Phase funktioniert nicht mit dem Trivialsort. Hier werden nur zwei Vergleiche und zwei Vertauschnungen durchgeführtImplementieren der eigenen Algorithmen
Nutzen Sie die vorgebenen Klassen zum Testender eigener Algorithmen
- Erzeugen Sie eine eigene Klasse für den Sortieralgorithmus
- Sie können die Klasse TrivialSort übernehmen.
- Ändern Sie den Klassennamen
- Ändern Sie in der Methode algorithmus() den Namen des Algorithmus
- Implementieren Sie die Methode sortieren(int von, int bis) die ein bestimmtes Intervall der Folge sortiert
- Sie können die Klasse TrivialSort übernehmen.
- Ändern Sie in der Klasse MainSort in der Methode algorithmusWahl() den benutzten Algorithmus.
- Tipps: Nutzen Sie die Infrastruktur der Oberklasse Sortierer beim Testen
- istKleiner(int a, int b), istKleinerGleich(int a, int b) : Vergleichen Sie die Werte des Feldes indem Sie bei diesen beiden Methoden den jeweiligen Index angeben. Es wird ein Zähler gepflegt der die Anzahl der gesamten Vergleiche beim Sortiervorgang zählt!
- tausche(int i, int j): tauscht die Werte auf Index i mit dem Wert von Index j. Es wird ein Zähler gepflegt der die Anzahl der Vertauschungen zählt
- tZaehler(): Inkrementiert die Anzahl der Vertauschungen falls nicht die Methode tausche() verwendet wurde. Dieser Zähler ist multi-threading (mt) save!
- vglZaehler(): Inkrementiert die Anzahl der Vergleiche falls nicht die Methoden istKleiner() oder istKleinerGleich() verwendet werden. Dieser Zähler ist mt-save!
- druckenKonsole() : druckt das Feld in seiner aktuellen Sortierung aus.
- Tracing: Ihre Klasse mit dem Sortieralgorithmus erbt eine statische boolsche Variable geschwaetzig. Sie können diese Variable jederzeit setzem mit geschwaetzig=true. Es werden alle Vertauschungen und Vergleiche auf der Konsole ausgegeben:
Beim TrivialSort führt das Setzen dieser Variable zur folgenden Konsolenausgabe:
Phase 1: Einfacher Test mit 6 Elementen Algorithmus: Sortiere drei Werte Unsortiert: feld[0]=6 feld[1]=2 feld[2]=4 feld[3]=3 feld[4]=5 feld[5]=7 Vergleich:feld[1]<feld[0] bzw. 2<6 Getauscht:feld[0<->1];f[0]=2;feld[1]=6 Vergleich:feld[2]<feld[1] bzw. 4<6 Getauscht:feld[1<->2];f[1]=4;feld[2]=6 Zeit(ms): 0 Vergleiche: 2 Vertauschungen: 2. Fehler in Sortierung Sortiert: feld[0]=2 feld[1]=4 feld[2]=6 feld[3]=3 feld[4]=5 feld[5]=7 Keine Phase 2 (Stresstest) aufgrund von Fehlern...
Quellcode
Klasse MainSort.java
Warnung: Diese Klasse lädt die Algorithmen dynamisch. Sie funktioniert nur wenn
- Die Namen der Klassen beibehalten werden. Die Namen der Klassen werden als Zeichenkette angegeben. Die Namen müssen vorhanden sein und die Klasse muss übersetzt worden sein.
- Das Paket s2.sort bleibt. Wenn die Paketstruktur geändert wird muss auch die fett gedruckte Zeichenkette angepasst werden.
Die Klasse MainSort.java in GitHub.
Klasse Sortieren.java
Die Klasse Sortierer ist eine abstrakte Klasse die die Infrastruktur zum Sortieren zur Verfügung stellt.
- Sie verwaltet ein Feld von ganzen Zahlen (int).
- Sie stellt Operationen zum Vergleichen und Tauschen von Elementen zur Verfügung
- Sie hat Zähler für durchgeführte Vertauschungen
- Sie kann ein Feld auf korrekte Sortierung prüfen
- Sie kann das Feld mit neuen Zufallszahlen belegen
- Sie hat eine statische Variable geschwaetzig mit der man bei Bedarf jeden Vergleich und jede Vertauschung auf der Kommandozeile dokumentieren kann.
- Die Klasse verwendete mt-sichere Zähler vom Typ AtomicInteger bei parallelen Algorithmen. Diese Zähler sind langsamer aber Sie garantieren ein atomares Inkrement.
Die Klasse Sortierer.java in GitHub.
Die Klasse TrivialSort.java
Diese Klasse ist ein Platzhalter der nur die beiden ersten Elemente eines Intervalls sortieren kann.
Das Programm dient zum Testen des Beispiels und es zeigt den Einsatz der schon implementierten istKleiner() und tausche() Methoden die von der Oberklasse geerbt werden.
Die Klasse TrivialSort.java in GitHub.
- 8891 views
MainSort.java: Ein Testprogramm
MainSort.java: Ein TestprogrammKlasse MainSort.java
Warnung: Diese Klasse lädt die Algorithmen dynamisch. Sie funktioniert nur wenn
- Die Namen der Klassen beibehalten werden. Die Namen der Klassen werden als Zeichenkette angegeben. Die Namen müssen vorhanden sein und die Klasse muss übersetzt worden sein.
- Das Paket s2.sort bleibt. Wenn die Paketstruktur geändert wird muss auch die fett gedruckte Zeichenkette angepasst werden.
package s2.sort;
import java.lang.reflect.Constructor;
import java.lang.reflect.InvocationTargetException;
import java.util.Arrays;
/**
*
* @author sschneid
* @version 2.0
*/
public class MainSort {
private static String algorithmusName;
/**
*
* Das Hauptprogramm sortiert sechs Zahlen in Phase 1
* Phase 2 wird nur aufgerufen wenn der Sortieralgorithmus
* für die erste Phase korrekt war
* @param args
*/
public static void main(String[] args) {
if (args.length > 0)
algorithmusName = args[0];
else
algorithmusName="";
int zeit = 3;
System.out.println("Phase 1: Einfacher Test mit 6 Elementen");
boolean erfolg = phase1();
if (erfolg) {
System.out.println ("Phase 2: Stresstest");
System.out.print("Der Stresstest wird beendet nachdem mehr ");
System.out.println("als " + zeit + " Sekunden benötigt werden.");
phase2(zeit);
}
else {System.out.println("Keine Phase 2 (Stresstest) " +
"aufgrund von Fehlern...");}
}
/**
* Auswahl des Sortieralgorithmus
* @ param das zu sortierende Feld
* @ return der Sortieralgorithmus
*/
public static Sortierer algorithmusWahl(int[] feld) {
Sortierer sort= null;
// Wähle ein Sortieralgorithmus abhängig von der
// gewünschten Implementierung
String nameSortierKlasse;
if (algorithmusName.equals("")) {
algorithmusName = "TrivialSort";
//algorithmusName = "SelectionSort";
//algorithmusName = "InsertionSort";
//algorithmusName = "BubbleSort";
//algorithmusName = "QuickSort";
//algorithmusName = "QuickSortParallel";
}
Class<?> meineKlasse;
Constructor<?> konstruktor;
try {
// Dynamisches Aufrufen einer Klasse
// Hole Metainformation über Klasse
meineKlasse = Class.forName("s2.sort."+ algorithmusName);
// Hole alle Konstruktoren
Constructor[] konstruktoren = meineKlasse.getConstructors();
// Nimm den Ersten. Es sollte nure einen geben
konstruktor = konstruktoren[0];
// Erzeuge eine Instanz dynamisch
sort = (Sortierer) konstruktor.newInstance((Object)feld);
} catch (ClassNotFoundException ex) {
System.out.println("Klasse nicht gefunden. Scotty beam me up");
} catch (InstantiationException ex) {
System.out.println("Probleme beim Instantieren. Scotty beam me up");
} catch (IllegalAccessException ex) {
System.out.println("Probleme beim Zugriff. Scotty beam me up");
} catch (SecurityException ex) {
System.out.println("Sicherheitsprobleme. Scotty beam me up");
} catch (IllegalArgumentException ex) {
System.out.println("Falsches Argument. Scotty beam me up");
} catch (InvocationTargetException ex) {
System.out.println("Falsches Ziel. Scotty beam me up");
}
//sort.geschwaetzig = true;
return sort;
}
/**
* Sortiere 6 Zahlen
* @return wurde die Folge korrekt sortiert?
*/
public static boolean phase1() {
long anfangszeit = 0;
long t = 0;
int[] gz = new int[6];
gz[0] = 6;
gz[1] = 2;
gz[2] = 4;
gz[3] = 3;
gz[4] = 5;
gz[5] = 7;
Sortierer sort = algorithmusWahl(gz);
System.out.println("Algorithmus: " + sort.algorithmus());
System.out.println("Unsortiert:");
sort.druckenKonsole();
anfangszeit = System.nanoTime();
sort.sortieren(0, gz.length - 1);
t = System.nanoTime() - anfangszeit;
System.out.print(
" Zeit(ms): " + t / 1000000
+ " Vergleiche: " + sort.anzahlVergleiche()
+ " Vertauschungen: " + sort.anzahlVertauschungen());
boolean erfolg = sort.validierung();
if (erfolg) {System.out.println(". Korrekt sortiert");}
else {
System.out.println(". Fehler in Sortierung");
}
System.out.println("Sortiert:");
sort.druckenKonsole();
return erfolg;
}
/**
* Sortieren von zufallsgenerierten Feldern bis eine maximale
* Zeit pro Sortiervorgang in Sekunden erreicht ist
* @param maxTime
*/
public static void phase2(int maxTime) {
// Maximale Laufzeit in Nanosekunden
long maxTimeNano = (long) maxTime * 1000000000L;
long t = 0;
// Steigerungsfaktor für Anzahl der zu sortierenden Elemente
double steigerung = 2.0; // Faktor um dem das Feld vergrößert wird
int anzahl = 5; // Größe des initialen Felds
long anfangszeit;
int[] gz;
Sortierer sort;
System.out.println("Maximalzeit(s): " + maxTime);
while (t < maxTimeNano) {
// Sortiere bis das Zeitlimit erreicht ist
anzahl = (int) (anzahl * steigerung);
// Erzeugen eines neuen Feldes
gz = new int[anzahl];
for (int i = 0; i < gz.length; i++) {
gz[i] = 1;
}
sort = algorithmusWahl(gz);
sort.generiereZufallsbelegung();
sort.zaehlerRuecksetzen();
anfangszeit = System.nanoTime();
sort.sortieren(0, gz.length - 1);
t = System.nanoTime() - anfangszeit;
System.out.print(
sort.algorithmus() +
". Feldgroesse: " + anzahl + " Zeit(ms): " + t / 1000000 +
" Vergleiche: " + sort.anzahlVergleiche() +
" Vertauschungen: " + sort.anzahlVertauschungen());
if (sort.validierung()) {System.out.println(". Korrekt sortiert");}
else {
System.out.println(". Fehler in Sortierung");
break;
}
sort.zaehlerRuecksetzen();
}
}
}Die Quellen bei github.
- 4005 views
MainSort unvollständig
Die Implementierung der MainSort ist auf dieser Seite nicht ganz vollständig. Die Imports und ein Return-Statement fehlen. Auf github ist die Version richtig :-)
- Log in to post comments
Sortierer.java
Sortierer.javaDie Klasse Sortierer ist eine abstrakte Klasse die die Infrastruktur zum Sortieren zur Verfügung stellt.
- Sie verwaltet ein Feld von ganzen Zahlen (int).
- Sie stellt Operationen zum Vergleichen und Tauschen von Elementen zur Verfügung
- Sie hat Zähler für durchgeführte Vertauschungen
- Sie kann ein Feld auf korrekte Sortierung prüfen
- Sie kann das Feld mit neuen Zufallszahlen belegen
- Sie hat eine statische Variable geschwaetzig mit der man bei Bedarf jeden Vergleich und jede Vertauschung auf der Kommandozeile dokumentieren kann.
- Die Klasse verwendete mt-sichere Zähler vom Typ AtomicInteger bei parallelen Algorithmen. Diese Zähler sind langsamer aber Sie garantieren ein atomares Inkrement.
Implementierung
package s2.sort;
import java.util.concurrent.atomic.AtomicInteger;
/**
*
* @author sschneid
* @version 2.1
*/
public abstract class Sortierer {
/**
* Das zu sortierende Feld
*/
protected int[] feld;
private int maxWert = Integer.MAX_VALUE;
// Zähler für serielle Sortieralgorithmen
private long tauschZaehlerSeriell;
private long vergleichszaehlerSeriell;
// Zähler für paralelle Sortieralgorithmen
private AtomicInteger tauschZaehlerParallel;
private AtomicInteger vergleichszaehlerParallel;
/**
* Der Algorithmus arbeitet parallel
*/
private final boolean parallel;
/**
* erweiterte Ausgaben beim Sortieren
*/
public static boolean geschwaetzig = false;
/**
* Initialisieren eines Sortierers mit einem
* unsortierten Eingabefeld s
* @param s ein unsortiertes Feld
* @param p der Algorithmus is parallel implementiert
*/
public Sortierer(int[] s, boolean p) {
feld = s;
parallel = p;
if (parallel) {
tauschZaehlerParallel = new AtomicInteger();
vergleichszaehlerParallel = new AtomicInteger();
}
else {
tauschZaehlerSeriell = 0;
vergleichszaehlerSeriell = 0;
}
}
/**
* die Groesse des zu sortierenden Feldes
*/
public int feldgroesse() {
return feld.length;
}
/**
* Gibt ein Feldelement auf gegebenem Index aus
* @param index
* @return
*/
public int getElement(int index) {
return feld[index];
}
/**
* sortiert das Eingabefeld
* @param s ein unsortiertes Feld
*/
abstract public void sortieren(int startIndex, int endeIndex);
/**
* Eine Referenz auf das Feld
* @return
*/
public int[] dasFeld() {
return feld;
}
/**
* kontrolliert ob ein Feld sortiert wurde
* @return
*/
public boolean validierung() {
boolean korrekt;
int i = 0;
while (((i + 1) < feld.length) &&
(feld[i]<=feld[i + 1])) {i++;}
korrekt = ((i + 1) == feld.length);
return korrekt;
}
/**
* Liefert den Namen des implementierten Sortieralgorithmus
* @return
*/
abstract public String algorithmus();
/**
* Drucken des Feldes auf System.out
*/
public void druckenKonsole() {
for (int i = 0; i < feld.length; i++) {
System.out.println("feld[" + i + "]=" + feld[i]);
}
}
/**
* Anzahl der Vertauschungen die zum Sortieren benoetigt wurden
* @return Anzahl der Vertauschungen
*/
public long anzahlVertauschungen() {
if (parallel) return tauschZaehlerParallel.get();
else return tauschZaehlerSeriell;
}
/**
* Anzahl der Vergleiche die zum Sortieren benoetigt wurden
* @return Anzahl der Vergleiche
*/
public long anzahlVergleiche() {
if (parallel) return vergleichszaehlerParallel.get();
else return vergleichszaehlerSeriell;
}
/**
* vergleicht zwei Zahlen a und b auf Größe
* @param a
* @param b
* @return wahr wenn a kleiner b ist
*/
public boolean istKleiner(int a, int b) {
vglZaehler();
if (geschwaetzig) {
System.out.println("Vergleich:feld["+a+"]<feld["+b+"] bzw. " +
feld[a] +"<"+ feld[b]);}
return (feld[a]<(feld[b]));
}
/**
* vergleicht zwei Zahlen a und b auf Größe
* @param a
* @param b
* @return wahr wenn a kleiner oder gleich b ist
*/
public boolean istKleinerGleich(int a, int b) {
vglZaehler();
if (geschwaetzig) {
System.out.println("Vergleich:feld["+a+"]<=feld["+b+"] bzw. " +
feld[a] +">"+ feld[b]);}
return (feld[a]<=(feld[b]));
}
/**
* diese Methode zaehlt alle Vergleiche. Sie ist mt-sicher
* für alle Algorithmen die das parallel Flag gesetzt haben
*/
public void vglZaehler() {
if (parallel) vergleichszaehlerParallel.getAndIncrement();
else vergleichszaehlerSeriell++;
}
/**
* Tausche den Inhalt der Position a mit dem Inhalt der Position b
* @param a
* @param b
*/
public void tausche(int a, int b) {
tZaehler();
if (geschwaetzig)
System.out.println("Getauscht:feld["+a+"<->"+b+"];f["+a
+ "]="+feld[b]+";feld["+b+"]="+feld[a]);
int s = feld[a];
feld[a] = feld[b];
feld[b] = s;
}
/**
* diese Methode zaehlt alle Vertauschungen. Sie ist mt-sicher
* für alle Algorithmen die das parallel Flag gesetzt haben
*/
public void tZaehler() {
if (parallel) tauschZaehlerParallel.getAndIncrement();
else tauschZaehlerSeriell++;
}
/**
* Belege das Feld mit Zufallswerten. Alte Belegungen werden gelöscht!
*/
public void generiereZufallsbelegung() {
// Generiere neue Belegung
maxWert = 2 * feld.length;
for (int i = 0; i < feld.length; i++) {
feld[i]=(int)(Math.random() * (double) maxWert);
}
}
/**
* Setzt Zaehler für Vertauschungen und Vergleiche zurueck auf Null
*/
public void zaehlerRuecksetzen() {
if (parallel) {
tauschZaehlerParallel.set(0);
vergleichszaehlerParallel.set(0);
}
else {
tauschZaehlerSeriell = 0;
vergleichszaehlerSeriell = 0;
}
}
}
- 3781 views
TrivialSort.java
TrivialSort.javaDiese Klasse ist ein Platzhalter der nur die beiden ersten Elemente eines Intervalls sortieren kann.
Das Programm dient zum Testen des Beispiels und es zeigt den Einsatz der schon implementierten istKleiner() und tausche() Methoden die von der Oberklasse geerbt werden.
package s2.sort;
/**
*
* @author sschneid
* @version 2.0
*/
public class TrivialSort extends Sortierer{
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public TrivialSort(int[] s) { super(s,false); }
/**
* Diese Methode sortiert leider nur die beiden ersten Elemente
* auf der Position von und (von+1)
* @param von
* @param bis
*/
@Override
public void sortieren(int von, int bis) {
geschwaetzig = false;
int temp; // Zwischenspeicher
if (istKleiner(von+1,von)) {
tausche(von,von+1);
}
if (istKleiner(von+2,von+1)) {
tausche(von+1,von+2);
}
//druckenKonsole();
}
@Override
public String algorithmus() {
return "Sortiere drei Werte";
}
}
- 3133 views
Sortieren durch Auswahl (Selectionsort)
Sortieren durch Auswahl (Selectionsort)Beim Suchen durch Auswahl durchsucht man das jeweilige Feld nach dem kleinsten Wert und tauscht den Wert an der gefundenen Position mit dem Wert an der ersten Stelle.
Anschließend sucht man ab der zweiten Position aufsteigend nach dem zweitkleinsten Wert und tauscht diesen Wert mit dem Wert der zweiten Position.
Man fährt entsprechend mit der dritten und allen weiteren Positionen fort bis alle Werte aufsteigend sortiert sind.
Verfahren
- Man suche im Feld f[1] bis f[N] die Position i1 an der sich das Element mit dem kleinsten Schlüssel befindet und vertausche f[1] mit f[i1]
- Man suche im Feld f[2] bis f[N] die Position i2 an der sich das Element mit dem kleinsten Schlüssel befindet und vertausche f[2] mit f[i2]
- Man verfahre wie oben weiter für Position i3 bis iN-1
Beispiel
Ausgangssituation: Ein Feld mit 7 unsortierten Ganzzahlwerten (N=7)
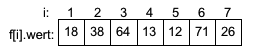
Die Zahl 12 auf Position 5 ist die kleinste Zahl im Feld f[1] bis f[7]. Somit ist i1=5. Nach Vertauschen von f[1] mit f[5] ergibt sich:
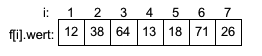
Die Zahl 13 auf Position 4 ist die kleinste Zahl im Feld f[2] bis f[7]. Somit ist i2=4. Nach Vertauschen von f[2] mit f[4] ergibt sich:
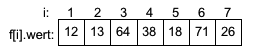
Die Zahl 18 auf Position 5 ist die kleinste Zahl im Feld f[3] bis f[7]. Somit ist i3=5. Nach Vertauschen von f[3] mit f[5] ergibt sich:
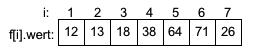
Das Verfahren wird entsprechend weiter wiederholt bis alle Werte sortiert sind.
Aufwand
Der minimale Aufwand Mmin(N), der maximale Aufwand Mmax(N) und er mittlere Aufwand Mmit(N) ist bei diesem naiven Verfahren gleich, da immer die gleiche Anzahl von Operationen (N-1) ausgeführt wird. Der Faktor 3 ensteht dadurch, dass bei einer Vertauschung zweier Werte insgesamt drei Operationen braucht:
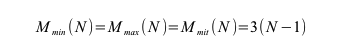
Die Anzahl der Vergleiche sind die Summe von n-1, n-1 etc. unabhängig davon ob das Feld sortiert oder unsortiert ist:
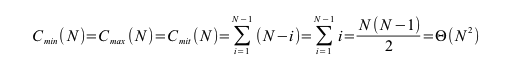
Implementierung
Die Implementierung der Klasse SelectionSort.java ist bei Github zu finden.
- 17245 views
Lautet das erste Element
Lautet das erste Element eines Feldes nicht f[0]?
Dann würde man dementsprechend ab der Position f[0] anfangen, das Feld zu durchsuchen!
- Log in to post comments
Antwort: Beginn einer Folge
Sehr gute Beobachtung,
Java fängt bei Null an zu zählen. Menschen beginnen oft bei Eins. Ich kann Ihnen da leider keine einfache Lösung bieten. Das ist Definitionssache. Man muß immer schauen was die Definition des ersten Elements ist.
- Log in to post comments
Selectionsort: Implementierung in Java
Selectionsort: Implementierung in JavaDie folgende Implementierung implementiert die abstrakte Klasse Sortierer die in den Beispielprogrammen zum Sortieren zu finden ist.
Implementierung: Klasse SelectionSort
package s2.sort;
/**
*
* @author sschneid
* @version 2.0
*/
public class SelectionSort extends Sortierer{
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public SelectionSort(int[] s) {super(s,false);}
/**
* sortiert ein Eingabefeld s und gibt eine Referenz auf dea Feld wieder
* zurück
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
@Override
public void sortieren(int startIndex, int endeIndex){
//geschwaetzig=true;
int minimumIndex;
for (int unteresEnde=startIndex; unteresEnde<endeIndex; unteresEnde++) {
minimumIndex = unteresEnde; //Vergleichswert
// Bestimme Position des kleinsten Element im Intervall
for (int j=unteresEnde+1; j<=endeIndex; j++) {
if (istKleiner(j,minimumIndex)) {
minimumIndex=j; // neuer Kandidat
}
}
// Tausche kleinstes Element an den Anfang des Intervalls
tausche(unteresEnde,minimumIndex);
// das kleinste Element belegt jetzt das untere Ende des Intervalls
}
}
/**
* Liefert den Namen des SelectionSorts
* @return
*/
@Override
public String algorithmus() {return "Sortieren durch Auswahl";}
}
- 8986 views
Sortieren durch Einfügen (Insertionsort)
Sortieren durch Einfügen (Insertionsort)Verfahren
Das Sortieren durch Einfügen ist ein intuitives und elementare Verfahren:
- Man teilt die zu sortierende Folge f mit N Elementen in eine bereits sortierte Teilfolge f[0] bis f[s-1] und in eine unsortierte Teilfolge f[s] bis f[n].
- Zu Beginn ist die sortierte Teilfolge leer.
- Der Beginn der unsortierten Folge f[s] wird die Sortiergrenze genannt.
- Man setzt eine Sortiergrenze hinter der bereits durch Zufall sortierte Teilfolge f[1] bis f[s-1]
- Vergleiche f[s] mit f[s-1] und vertausche die beiden Elemente falls f[s]<f[s-1]
- Führe weitere Vergleiche und absteigende Vertauschungen durch bis man ein f[s-j] gefunden hat für das gilt f[s-j-1]<f[s-j]
- Erhöhe die Sortiergrenze von f[i] auf f[i+1] und wiederhole die Vergleichs- und Vertauschungsschritte wie im vorhergehenden Schritt beschrieben.
- Die Folge ist sortiert wenn die Sortiergrenze das Ende des Folge erreicht hat.
Beispiel
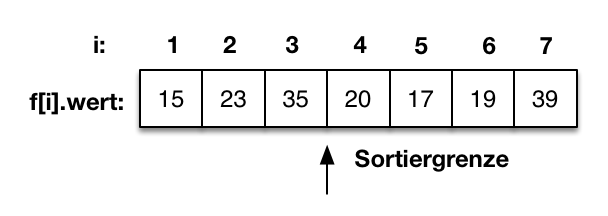 |
Gegeben sei eine Folge in einem Feld mit sieben Elementen. Die ersten drei Elemente sind bereits sortiert und die Sortiergrenze wird mit 4 belegt. Die unsortierte Folge beginnt auf dem Feldindex vier. |
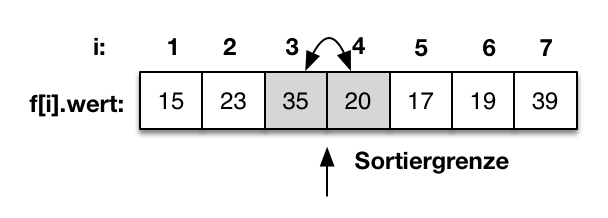 |
Als erstes wird der Wert f[4]=20 mit f[3]=35 verglichen. Da f[4] größer als f[3] ist, werden die beiden Werte getauscht. |
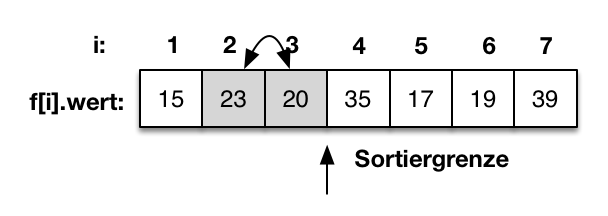 |
Anschließend folgt der Vergleich von f[3]=20 mit f[2]=23. Der Wert von f[3] ist größer als f[2]. Die beiden Werte werden getauscht. |
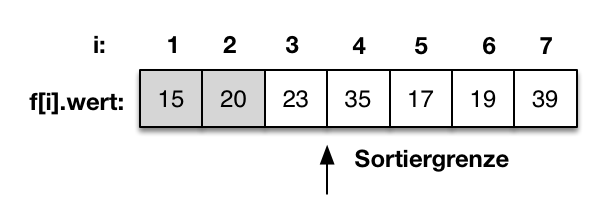 |
Der Vergleich von f[2] mit f[1] zeigt, dass f[2] größer als f[1] ist. f[2]=20 hat also seine korrekte Position in der sortierten Teilfolge gefunden. |
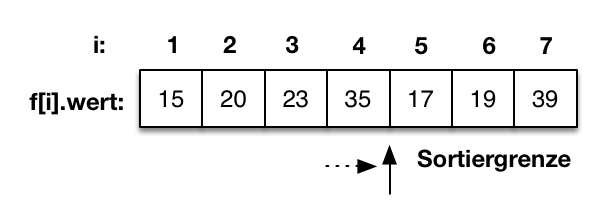 |
Der aktuelle Durchlauf ist hiermit beendet. Die Sortiergrenze wird um eins erhöht und erhält den Wert 5. |
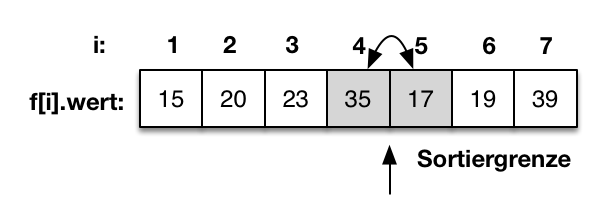 |
Die sortierte Teilfolge ist um eins größer geworden. Es wird wieder f[5]=17 mit f[4]=35 verglichen. Da f[5] größer als f[4] ist, werden die beiden Werte getauscht. Jeder Durchlauf endet, wenn der Wert nicht mehr getauscht werden muss. Der Algorithmus endet wenn die Sortiergrenze die gesamt Folge umfasst. |
Aufwand
Das Sortieren durch Einfügen braucht im günstigsten Fall nur N-1 Vergleiche für eine bereits sortierte Folge. Im ungünstigsten Fall (fallend sortiert) ist aber ein quadratisches Aufwand nötig.
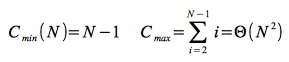
Das gleiche gilt für die Vertauschungen. Hier müssen im ungünstigsten Fall Vertauschungen in einer quadratischen Größenordnung durchgeführt werden.
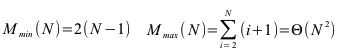
Implementierung
Die Implementierung der Klasse InsertionSort.java ist bei Github zu finden.
- 14003 views
Insertionsort: Implementierung in Java
Insertionsort: Implementierung in JavaDie folgende Implementierung implementiert die abstrakte Klasse Sortierer die in den Beispielprogrammen zum Sortieren zu finden sind.
Implementierung: Klasse InsertionSort
package s2.sort;
/**
*
* @author sschneid
* @version 2.0
*/
public class InsertionSort extends Sortierer {
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public InsertionSort(int[] s) {
super(s,false);
}
/**
* sortiert ein Feld im Bereich startIndex bis endeIndex
* @param startIndex
* @param endeIndex
*/
public void sortieren(int startIndex, int endeIndex) {
for (int sortierGrenze = startIndex;sortierGrenze < endeIndex;
sortierGrenze++) {
int probe = sortierGrenze + 1;
int j = startIndex;
while (istKleiner(j, probe)) {
j++;
}
// Verschiebe alles nach rechts.
// Tausche den Probenwert gegen den unteren Nachbarn
// bis man bei der Position j angekommen ist
for (int k = probe - 1; k >= j; k--) {
tausche(k, k + 1);
}
}
}
/**
* Liefert den Namen des Insertion Sorts
* @return
*/
public String algorithmus() {
return "Sortieren durch Einfuegen";
}
}
- 6423 views
Bubblesort
BubblesortDer Bubblesort hat seinen Namen von dem Prinzip erhalten, dass der größte Wert eine Folge durch Vertauschungen in der Folge austeigt wie eine Luftblase im Wasser.
Verfahren
- Vergleiche in aufsteigender Folge die Werte einer unsortierten Folge und vertausche die Werte wenn f(i) > f(i+1) ist
- Wiederhole die Vergleiche und eventuell nötige Vertauschungen bis keine Vetauschung bei einem Prüfdurchlauf vorgenommen werden muss.
Beispiel
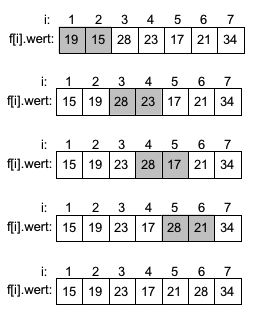 |
Es werden die Werte aufsteigen auf ihre korrekte Reihenfolge verglichen. Im ersten "Durchlauf" müssen die Werte 19 und 15 (in grau) getauscht werden. Anschließend werden die Werte 28 und 23 getauscht und im nächsten Schritt die Werte 28 und 17. Die letzte Vertauschung findet zwischen 28 auf Position 5 und 21 auf Position 6 statt. Der erste Durchlauf ist beendet und der zweite Durchlauf beginnt mit den Vergleichen ab Index 1. |
| Im zweiten Durchlauf sind die Werte auf Index 1 und 2 in der richtigen Reihenfolge. Die Werte 23 und 17 sind die ersten die getauscht werden müssen. Der Wert 23 steigt weiter auf und wird noch mit dem Wert 21 getauscht. Die letzten beiden Werte auf Index 6 und 7 sind in der richtigen Reihenfolge und müssen nicht getauscht werden. Der zweite Durchlauf ist beendet. | 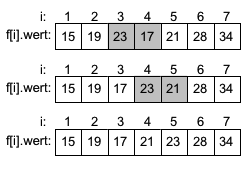 |
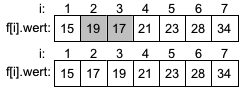 |
Im dritten Durchlauf muß die 19 auf Position 2 mit der 17 auf Position 3 getauscht werden. Auf den höheren Positionen sind keine Veratuschungen mehr nötig. |
Der vierte Durchlauf ist der letzte Durchlauf. In ihm finden keine weiteren Vertauschungen statt. Alle Elemente sind aufsteigend sortiert. Der Algorithmus bricht nach dem vierten Durchlauf ab, da keine Vertauschungen nötig waren. Alle Elemente sind sortiert.
Aufwand
Der günstigste Fall für den Bubblesort ist eine sortierte Folge. In diesem Fall müssen nur N-1 Vergleiche und keine Vertauschungen vorgenommen werden.
Ungünstige Fälle sind fallende Folgen. Findet man das kleinste Element auf dem höchsten Index sind N-1 Durchläufe nötigt bei denen das kleinste Element nur um eine Position nach vorne rückt.
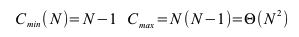
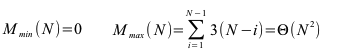
In ungünstigen Fällen ist der Aufwand N2. Man kann zeigen, dass der mittlere Aufwand bei N2 liegt:
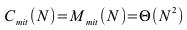
Effizienzsteigerungen
Es gibt eine Reihe von Verbesserungen die darauf beruhen, dass man nicht bei jedem Durchlauf in der ganzen Folge die Nachbarn vergleichen muss. Nach dem ersten Durchlauf ist das größte Element auf dem Index N angekommen. Man muss im nächsten Durchlauf also nur noch alle Nachbarn bis zur Position N-1 kontrollieren.
Implementierung
Die Implementierung der Klasse BubbleSort.java ist bei Github zu finden.
- 7836 views
BubbleSort: Implementierung in Java
BubbleSort: Implementierung in JavaDie folgende Implementierung implementiert die abstrakte Klasse Sortierer die in den Beispielprogrammen zum Sortieren zu finden sind.
Implementierung: Klasse BubbleSort
package s2.sort;
/**
*
* @author sschneid
* @version 2.0
*/
public class BubbleSort extends Sortierer {
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public BubbleSort(int[] s) {super(s, false); }
/**
* sortiert ein Eingabefeld s und gibt eine Referenz auf dea Feld wieder
* zurück
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
public void sortieren(int startIndex, int endeIndex) {
boolean vertauscht;
do {
vertauscht = false;
for (int i = startIndex; i+1 <= endeIndex; i++) {
if (istKleiner(i + 1,i)) {
tausche(i,i+1);
vertauscht = true;
}
}
} while (vertauscht);
}
/**
* Liefert den Namen des Bubble Sorts
* @return
*/
public String algorithmus() {
return "Bubble Sort";
}
}
- 5773 views
Quicksort: Sortieren durch rekursives Teilen
Quicksort: Sortieren durch rekursives TeilenDer Quicksort ist ein Verfahren welches auf dem Grundprinzip des rekursiven Teilens basiert:
- Man nimmt ein beliebiges Pivotelement als Referenz (Pivotpunkt: Drehpunkt, Angelpunkt)
- Man teilt die unsortierte Folge in drei Unterfolgen
- Alle Elemente die kleiner oder gleich dem Pivotelement sind
- Das Pivotelement
- Alle Element die größer oder gleich dem Pivotelement sind
Die Unterfolgen die größer bzw. kleiner als das Pivotelement sind, sind selbst noch unsortiert. Das Pivotelement steht bereits an der richtigen Position zwischen den zwei Teilfolgen.
Durch rekursives Sortieren werden auch sie sortiert.
Der Quicksort wurde 1962 von C.A.R. Hoare (Computer Journal) veröffentlicht.
Verfahren
- Folgen die aus keinem oder einem Element bestehen bleiben unverändert.
- Wähle ein Pivotelement p der Folge F und teile die Folge in Teilfolgen F1 und F2 derart das gilt:
- F1 enhält nur Elemente von F ohne das Pivotelement p die kleiner oder gleich p sind
- F2 enhält nur Elemente von F ohne das Pivotelement p die größer oder gleich p sind
- Die Folgen F1 und F2 werden rekursiv nach dem gleichen Prinzip sortiert
- Die Ergebnis der Sortierung ist eine Aneinanderreihung der der Teilfolgen F1, p, F2.
Anmerkung: Der Quicksort folgt dem allgemeinen Prinzip von "Teile und herrsche" (lat.: "Divide et impera", engl. "Divide and conquer")
Beispiel
Im ersten Schritt wird das vollständige Feld vom Index 1 bis 7 sortiert, indem der Wert 23 auf dem Index 7 als Pivotwert (Vergleichswert) gewählt.
Es wird nun vom linken Ende des Intervals (Index 1) aufsteigend das erste Element gesucht welches größer als das Pivotelement ist. Hier ist es der Wert 39 auf dem Index 2. Anschließend wird vom oberen Ende des Intervals von der Position links vom Pivotelement absteigend das erste Element gesucht welches kleiner als das Pivotelement ist. Hier ist es der Wert 19 auf dem Index 6.
Im nächsten Schritt werden die beiden gefundenen Werte getauscht und liegen nun in der "richtigen" Teilfolge.
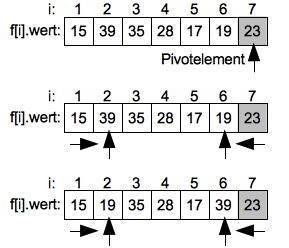
Jetzt wird die Suche von links nach rechts weitergeführt bis das nächste Element gefunden ist welches größer als das Pivotelement ist. Hier ist es 35 auf Position 3. Die fallende Suche von Rechts endet bei dem Wert 17 auf Index 5. Die beiden Werte werden dann getauscht.
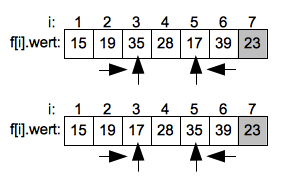
Nach der Vertauschung wird die aufsteigende Suche von Links weitergeführt und endet beim Wert 28 auf dem Index 4. Die fallende Suche von Rechts endet sofort da der Suchindex der steigenden Suche erreicht ist.
Der Pivotwert 23 auf Index 7 wird jetzt mit 28 auf dem Index getauscht und hat seine korrekte Endposition erreicht.
Der Sortiervorgang wird jetzt rekursiv im Intervall 1 bis 3 und 5 bis 7 fortgeführt. Wie zuvor werden die Werte auf dem höchsten Index der Unterintervalle wieder als Pivotwerte gewählt.
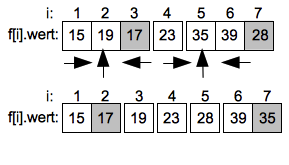
Im linken Unterintervall endet die aufsteigende Suche schnell beim Wert 19 auf Index 2 der dann mit dem Pivotwert 17 getauscht wird. Im rechten Unterintervall muss bei der aufsteigenden suche der Wert 35 auf Index 5 mit dem Pivotwert 28 getauscht werden.
Bei den weiteren Teilungen in Unterintervalle bleiben nur noch das Intervall von Index 1 bis 2 sowie das Intervall von Index 6 bis 7 übrig. Hier werden wieder die Elemente am rechten Rand als Pivotwerte gewählt.
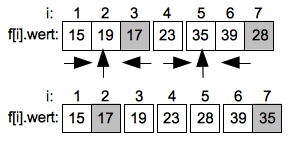
Im linken Unterintervall durchläuft die aufsteigende Suche das einzige Element und endet ohne Vertauschung. Im rechten Intervall muss ein letztes mal der Wert 39 mit 35 getauscht werden.
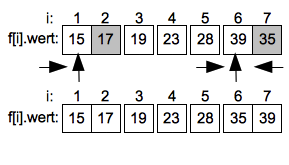
Aufwand
Der Quicksort ist in normalen Situationen mit einem Aufwand von n*log(n) sehr gut für große Datenmengen geeignet. Er ist einer der schnellsten Algorithmen. Bei sehr ungünstigen Sortierfolgen (schon sortiert) kann er aber auch mit einem quadratischen Aufwand sehr ineffizient sein.
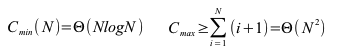
Vorsortierte Folgen sind durchaus häufig bei realen Problemen zu finden. Der Quicksort ist bei schon sortierten Folgen sehr ineffizient ist und daher ist der Einsatz bei realen Anwendungen durchaus heikel.
Implementierung
Serieller Quicksort
Die Implementierung der Klasse QuickSort.java ist bei Github zu finden.
Parallelisierter Quicksort
Die unten aufgeführte Klasse nutzt die "Concurrency Utilities" die in Java 7 eingeführt wurden. Aus der Sammlung wird das Fork/JoinFramework verwendet. Die Implementierung der Klasse QuickSortParallel.java ist bei Github zu finden.
Das Aufteilen des Sortierintervalls erfolgt hier seriell in einer eigenen Methode.
Das Sortieren der Teilintervalle erfolgt parallel solange das Intervall eine bestimmte Mindestgröße (100) besitzt.
Die Fork/Join Klassen stellen dem Algorithmus einen Pool von Threads zur Verfügung die sich nach der Anzahl des Prozessoren des Rechners richten.
Hierzu dient eine Spezialisierung der Klasse RecursiveAction.
- Die Methode compute() wird in einem eigenen Thread durchgeführt wenn das dazugehörige Objekt mit der Methode invokeAll()aufgerufen wird. Diese Methode wird überschrieben.
- Die Methode invokeAll() erlaubt es neue Tasks zu in Auftrag zu geben. Diese Methode wird erst beendet wenn alle Tasks ausgeführt sind.
In der vorliegenden Implementierung erfolgt ein paralleler Aufruf eines Task zum Sortieren der Teilintervalle und nicht ein sequentieller Methodenaufruf.
Die Implementierung des Task erfolgt in der inneren Klasse Sorttask. Diese Klasse ummantelt quasi die Sortiermethode.
- 13270 views
Verfahren
Im Abschnitt "Verfahren" wird das Pivotelement zuerst "p" genannt. Im weiteren Verlauf wird jedoch "k" als Pivotelement bezeichnet. Richtig müsste es aber auch "p" heißen, oder?
Folgen die aus keinem oder einem Element bestehen bleiben unverändert.
Wähle ein Pivotelement p der Folge F und teile die Folge in Teilfolgen F1 und F2 derart das gilt:
F1 enhält nur Elemente von F ohne das Pivotelement k die kleiner oder gleich k sind
F2 enhält nur Elemente von F ohne das Pivotelement k die größer oder gleich k sind
Die Folgen F1 und F2 werden rekursiv nach dem gleichen Prinzip sortiert
Die Ergebnis der Sortierung ist eine Aneinanderreihung der der Teilfolgen F1, k, F2.
- Log in to post comments
typo
Beispiel
[...](nach dem zweiten Bild)
Der Pivotwert 23 auf Index 7 wird jetzt mit 28 auf dem Index getauscht und hat seine korrekte Endposition erreicht.
[...]
Aufwand
Der Quicksort ist in normalen Situationen mit einem Aufwand von n*log(n) sehr gut für große Datenmengen geeignet. Er ist einer der schnellsten Algorithmen. Bei sehr ungünstigen Sortierfolgen (schon sortiert) kann er aber auch mit einem quadratischen Aufwand sehr ineffizient sein.
- Log in to post comments
Verfahren (Intervallbildung)
Sie beschreiben das Ergebnis des Teilsortierverfahres als eine Aneinanderreihung von F1, p, F2 (also quasi 3 Intervalle).
Nachdem 17 aber in dem linken Teilintervall als Pivotelement für die weitere Ausführung verwendet wird, ist 17 also p kein eigenes Teilintervall sondern laut ihrer Darstellung Teil des Intervalls 15,17. Wie kommt das?
- Log in to post comments
Sehr gut beobachtet
Das Pivotelement kann ein kleines Intervall bilden. Es steht halt zwischen den beiden großen Intervallen. Schlechte Erklärung meiner Seite.
Ein Gedankenexperiment:
* Ein anderes Element kann den gleichen Schlüssel wie das Pivotelement haben. Das wurde in den Beispielen nie durchgespielt...
* Gleich ob man mit ,>= tested, das andere Element gehört zum Intervall links oder rechts.
* Deswegen sollte auch das Pivotelement so behandelt werden. Es gehört in das linke oder rechte Intervall.
* Das mittlere Intervall macht nicht richtig Sinn.
Das dritte Intervall macht auch keinen Unterschied bei der Komplexität des Algorithmus. Es ist sehr klein im vergleich zu den beiden anderen Intervallen. Ich würde es als eine Variante akzeptieren.
- Log in to post comments
Quicksort: Implementierung in Java
Quicksort: Implementierung in JavaDie folgende Implementierung implementiert die abstrakte Klasse Sortierer die in den Beispielprogrammen zum Sortieren zu finden sind.
Implementierung: Klasse Quicksort
package s2.sort;
/**
*
* @author sschneid
*/
public class QuickSort extends Sortierer{
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public QuickSort(int[] s) {
super(s,false);
}
/**
* sortiert ein Eingabefeld s und gibt eine Referenz auf dea Feld wieder
* zurück
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
@Override
public void sortieren(int startIndex, int endeIndex) {
int i = startIndex;
int j = endeIndex;
int pivotWert = feld[startIndex+(endeIndex-startIndex)/2];
//System.out.println("von"+ startIndex+", bis:"+endeIndex +
// " pivot:" + pivotWert);
while (i<=j) {
// Suche vom unteren Ende des Bereichs aufsteigend einen
// Feldeintrag welcher groesser als das Pivotelement ist
while (feld[i] < pivotWert) {i++;vglZaehler();}
// Suche vom oberen Ende des Bereichs absteigend einen
// Feldeintrag der kleiner als das Pivotelement ist
while (feld[j] > pivotWert) {j--;vglZaehler();}
// Vertausche beide Werte falls die Zeiger sich nicht
// aufgrund mangelnden Erfolgs überschnitten haben
if (i<=j) {
tausche(i,j);
i++;
j--;
}
}
// Sortiere unteren Bereich
if (startIndex<j) {sortieren(startIndex,j);}
// Sortiere oberen Bereich
if (i<endeIndex) {sortieren(i,endeIndex);}
}
/**
* Liefert den Namen des Insertion Sorts
* @return
*/
@Override
public String algorithmus() {
return "QuickSort";
}
}
Implementierung: Parallelisierter Quicksort
Die unten aufgeführte Klasse nutzt die "Concurrency Utilities" die in Java 7 eingeführt wurden. Aus der Sammlung wird das Fork/Join Framework verwendet.
Das Aufteilen des Sortierintervalls erfolgt hier seriell in einer eigenen Methode.
Das Sortieren der Teilintervalle erfolgt parallel solange das Intervall eine bestimmte Mindestgröße (100) besitzt.
Die Fork/Join Klassen stellen dem Algorithmus einen Pool von Threads zur Verfügung die sich nach der Anzahl des Prozessoren des Rechners richten.
Hierzu dient eine Spezialisierung der Klasse RecursiveAction.
- Die Methode compute() wird in einem eigenen Thread durchgeführt wenn das dazugehörige Objekt mit der Methode invokeAll() aufgerufen wird. Diese Methode wird überschrieben.
- Die Methode invokeAll() erlaubt es neue Tasks zu in Auftrag zu geben. Diese Methode wird erst beendet wenn alle Tasks ausgeführt sind.
In der vorliegenden Implementierung erfolgt ein paralleler Aufruf eines Task zum Sortieren der Teilintervalle und nicht ein sequentieller Methodenaufruf.
Die Implementierung des Task erfolgt in der inneren Klasse Sorttask. Diese Klasse ummantelt quasi die Sortiermethode.
package s2.sort;
import java.util.concurrent.ForkJoinPool;
import java.util.concurrent.RecursiveAction;
/**
*
* @author sschneid
* @version 2.0
*/
public class QuickSortParallel extends Sortierer{
static int SIZE_THRESHOLD=100; // Schwellwert für paralleles Sortieren
private static final ForkJoinPool THREADPOOL = new ForkJoinPool();
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist parallel (true Argument)
* @param s
*/public QuickSortParallel(int[] s) {
super(s, true);
}
/**
* Innere statische Klasse die Fork and Join aus dem Concurrency package
* implementiert. Sie macht aus Methodenaufrufen, Taskaufrufe von Threads
*/
static class SortTask extends RecursiveAction {
int lo, hi;
QuickSortParallel qsp;
/**
* Speichere alle wichtigen Parameter für den Task
* @param lo untere Intervallgrenze
* @param hi obere Intervallgrenze
* @param qsp Referenz auf das zu sortierende Objekt
*/
SortTask(int lo, int hi, QuickSortParallel qsp) {
this.lo = lo;
this.hi = hi;
this.qsp =qsp;
}
/**
* Führe Task in eigenem Thread aus und nutze Instanzvariablen
* als Parameter um Aufgabe auszuführen.
*/
@Override
protected void compute() {
//System.out.println(" Thread ID => " + Thread.currentThread().getId());
if (hi - lo < SIZE_THRESHOLD) {
// Sortiere kleine Intervalle seriell
qsp.sortierenSeriell(lo, hi);}
else { // Sortiere große Intervalle parallel
int obergrenzeLinkesIntervall;
obergrenzeLinkesIntervall = qsp.teilsortieren(lo,hi);
// der serielle rekursive Aufruf wird ersetzt durch
// den parallelen Aufruf zweier Threads aus dem Threadpool
//System.out.println("Parallel: "+
// lo+","+obergrenzeLinkesIntervall+","+hi);
invokeAll(new SortTask(lo,obergrenzeLinkesIntervall,qsp),
new SortTask(obergrenzeLinkesIntervall+1,hi,qsp));
}
}
}
/**
* sortiert ein Eingabefeld s und gibt eine Referenz auf dea Feld wieder
* zurück
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
@Override
public void sortieren(int startIndex, int endeIndex) {
THREADPOOL.invoke(new SortTask(startIndex,endeIndex,this));
}
/**
* sortiert ein Eingabefeld s und gibt eine Referenz auf dea Feld wieder
* zurück
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
public void sortierenSeriell(int startIndex, int endeIndex) {
if (endeIndex > startIndex) {
int obergrenzeLinkesIntervall= teilsortieren(startIndex, endeIndex);
//System.out.println("Seriell: "+
// startIndex+","+obergrenzeLinkesIntervall+","+endeIndex);
// Sortiere unteren Bereich
if (startIndex<obergrenzeLinkesIntervall) {
sortierenSeriell(startIndex,obergrenzeLinkesIntervall);}
// Sortiere oberen Bereich
if (obergrenzeLinkesIntervall+1<endeIndex) {
sortierenSeriell(obergrenzeLinkesIntervall+1,endeIndex);}
}
}
public int teilsortieren(int startIndex, int endeIndex) {
int i = startIndex;
int j = endeIndex;
int pivotWert = feld[startIndex+(endeIndex-startIndex)/2];
//druckenKonsole();
while (i<=j) {
// Suche vom unteren Ende des Bereichs aufsteigend einen
// Feldeintrag welcher groesser als das Pivotelement ist
while (feld[i] < pivotWert) {i++;vglZaehler();}
// Suche vom oberen Ende des Bereichs absteigend einen
// Feldeintrag der kleiner als das Pivotelement ist
while (feld[j]> pivotWert) {j--;vglZaehler();}
// Vertausche beide Werte falls die Zeiger sich nicht
// aufgrund mangelnden Erfolgs überschnitten haben
if (i<=j) {
tausche(i,j);
i++;
j--;
}
}
//System.out.println("von"+ startIndex+", bis:"+endeIndex +
// " pivot:" + pivotWert + " , return: " +i);
return i-1;
}
/**
* Liefert den Namen des Insertion Sorts
* @return
*/
public String algorithmus() {
return "QuickSort mit Fork and Join";
}
}
Hinweis: Dieser Algorithmus ist parallel. Er teilt dies der Oberklasse im Konstruktor als Parameter mit. Hierdurch werden die Zähler für die Vergleiche von Vertauschungen und Vergleichen vor einem parallelen Inkrement geschützt. Die Synchronisierung dieser Zählvariablen ist leider so aufwendig, dass der Algorithmus nicht mehr schneller als der seriell Algorithmus ist...
Man muss hier leider eine Entscheidung treffen:
- setzen des Flag auf true: Die Vertauschungen werden korrekt gezählt. Der Algorithmus ist korrekt und langsam.
- setzen des flag auf false: Die Veretauschungen und Vergleiche werden nicht korrekt gezählt. Der Algorithmus ist korrekt und schnell. Das bedeutet, er skaliert auf Mehrprozessorsystemen.
- 8229 views
Übung (Quicksort)
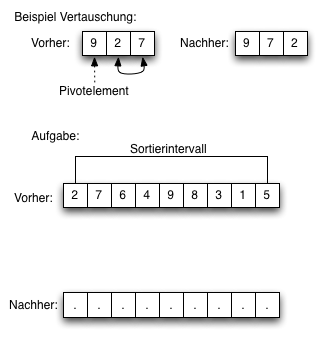
Übung (Quicksort)Führen Sie einen Durchlauf des Quicksorts manuell durch. Teilen Sie ein gegebenes Sortierintervall (Aufgabe: Vorher) nach den Regeln des Quicksorts in zwei Unterintervalle die noch sortiert werden müssen.
- Sortieren Sie aufsteigend
- Wählen Sie das Pivotelement ganz rechts im Intervall.
- Markieren Sie das Pivotelement in der Aufgabe mit einem Pfeil von unten (siehe Beispiel).
- Wenden Sie die Regeln des Quicksorts an. Zeichnen Sie zweiseitige Pfeile im "Vorher" Diagramm ein, um die notwendigen Vertauschungen zu markieren.
- Zeichnen Sie mit einem zweiseitigen Pfeil die nötige Vertauschung des Pivotelements im "Vorher" Diagramm ein.
- Tragen Sie alle neuen Werte im "Nachher" Diagramm ein.
- Zeichnen sie die beiden verbliebenen zu sortierenden Zahlenintevalle mit eckigen Linien (siehe "Vorher" Diagramm) ein.
- 7756 views
Lösung (Quicksort)
Lösung (Quicksort) 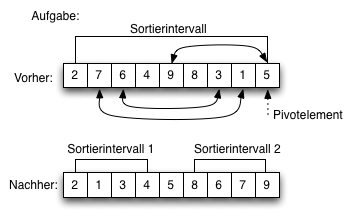
- 5271 views
Heapsort
HeapsortDer Heapsort (Sortieren mit einer Halde) ist eine Variante des Sortierens durch Auswahl. Er wurde in den 1960er Jahren von Robert W. Floyd und J. W. J. Williams entwickelt (siehe: Artikel in Wikipedia).
Der Heapsort hat den Vorteil, dass er auch im ungünstigsten Fall in der Lage ist mit einem Aufwand von O(N*log(N)) zu sortieren.
Hierfür wird eine Datenstruktur (der Heap) verwendet mit der die Bestimmung des Maximums einer Folge in einem Schritt möglich ist.
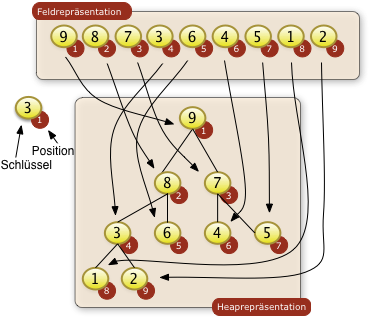 |
Beim Heapsort werden die zu sortierenden Schlüssel einer Folge in zwei Repräsentation betrachet:
Beide Repräsentationen sind Sichten auf die gleichen Daten. Beim Heapsort werden nicht die Schlüssel in einen Binärbaum umkopiert. Die Heaprepräsentation dient nur dem Betrachter zur Verdeutlichung der Beziehung gewisser Feldpositionen. Die Grundidee des Heapsorts besteht darin, daß an der Wurzel des Binärbaums immer der größte Schlüssel stehen muss. Diesen größten Schlüssel kann man dann dem Binärbaum entnehmen und als größtes Element der Folge benutzen. Die verbliebene unsortierte Teilfolge muss dann wieder so als ein Baum organisiert werden in dem das größte Element an der Wurzel steht. Durch sukzessives Entnehmen der verbliebenen gößten Elemente kann man die gesamte Folge sortieren. |
Beim Heapsort muss nicht nur an der Wurzel des Baums der größte Schlüssel stehen. Jeder Knoten im Binärbaum muss größer als die Unterknoten sein. Diese Bedingung nennt man die Heapbedingung.
Verfahren
Beim Heapsort wird auf eine Feld mit N unsortierten Schlüsseln das folgende Verfahren wiederholt angewendet:
- Herstellen der Heapbedingung durch das Bootom-Up für ein Feld mit N Schlüsseln
- Tauschen des ersten und größten Schlüssels auf der Position 1 mit dem letzten unsortierten Schlüssel auf Position N.
- Wiederherstellen des Heapbedingung durch Versickern (Top-Down Verfahren)
- Wiederholen des Verfahrens für die Positionen 1 bis N-1. Ab der Position N ist das Feld schon sortiert.
Beispiel
| Grafische Visualisierung | Beschreibung |
|---|---|
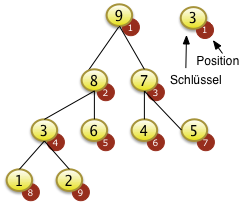 |
Das Beispiel links zeigt nicht eine vollständige Sortierung der gesamten Folge. Es zeigt nur das Einsortieren eines Elements für eine Feldstruktur die schon der Heapbedingung genügt. Das Feld mit den N=9 Elementen wurde so vorsortiert, dass es der Heapdebingung genügt. Das Herstellen der Heapbedingung wird später erläutert. |
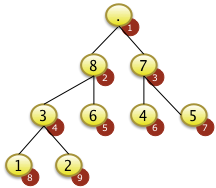 |
Das Element mit dem Schlüssel 9 wird von der Spitze des Baums f[1] entfernt... |
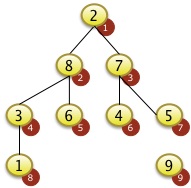 |
... und mit dem Wert 2 der Position N=9 getauscht. Der größte Schlüssel der Folge befindet sich jetzt auf der Position 9. Alle Elemente ab f[9]= F[N] aufwärts sind jetzt aufsteigend sortiert. Alle Elemente von f[1] bis f[N-1]=f[8] sind unsortiert und müssen noch sortiert werden. Die Elemente von f[1] bis f[8] genügen auch nicht mehr der Heapbedingung. Der Wert f[1]=2 ist nicht größer als f[2]=8 oder f[3]=7 |
Weitere Ressourcen
- Sehr schöne Visualisierung der Universität San Francisco (gefunden von der WIMBIT20A!)
Implementierung
Die Implementierung der Klasse HeapSort.java ist bei Github zu finden.
- 5815 views
Die Heapbedingung
Die HeapbedingungEin Feld f[1] bis f[N] mit Schlüsseln bildet einen Heap wenn die folgende Bedingung gilt:
| Heapbedingung |
|---|
|
f[i]<=f[i/2] für 2<= i <= N] |
Die Heapbedingung lässt sich leichter grafisch in einer Baumdarstellung verdeutlichen:
 |
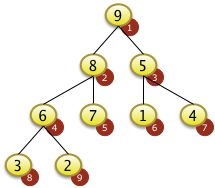
Das Feld f mit der Feldgröße N=9
genügt der Heapbedingung da jeder obere Knoten größer als die beiden Unterknoten ist. Die Position im Feld wird hier in rot dargestellt. Der Schlüssel (Wert) des Feldelements hat einen gelben Hintergrund |
- 5196 views
Herstellen der Heapbedingung für einen unsortierten Heap (Bottom-Up Methode)
Herstellen der Heapbedingung für einen unsortierten Heap (Bottom-Up Methode)Mit dem Bottom-Up Verfahren kann man die Heapbedingung für vollständig unsortierte Folgen von Schlüsseln herstellen.
Das Verfahren basiert auf der Idee, dass beginnend mit dem Schlüssel auf der höchsten Feldposition f[N] der Wert versickert wird um anschließend den nächst niedrigeren Wert F[N-1] zu versickern bis man den größten Wert f[1] versickert hat.
Beispiel
| Grafische Visualisierung | Beschreibung |
|---|---|
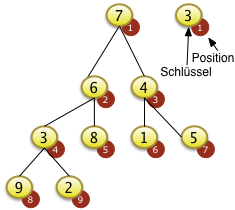 |
Der gegebene Baum sei vollständig mit Zufallsschlüsseln belegt. Alle Werte sind zufällig. Die Positionen 5, 6,7,8 und 9 können nicht versickert werden, da sie keine Unterblattknoten zum Versickern haben. |
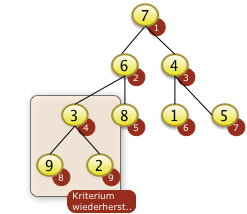 |
Das Bottom-Up Verfahren beginnt mit dem ersten Knoten i der über Unterknoten verfügt. Dieser Knoten ist immer die Position N/2 abgerundet. Bei N=9 ist die 9/2= 4.5. Der abgerundete Wert ist i=4. Hier muß f[8]=9 mit f[4]=3 getauscht werden um den Schlüssel zu versickern. |
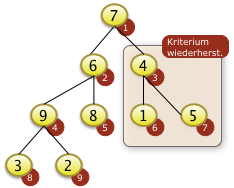 |
Bei i=3 muss f[3]=4 mit f[7]=5 getauscht werden und ist damit auch versickert. |
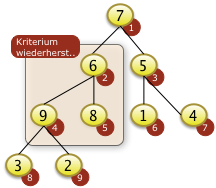 |
Bei i=2 muss f[4] mit f[2] getauscht werden. Das rekursives Versickern bei f[4]=9 is nicht notwendig. f[4]=9 ist größer als f[8]=3 und f[9]=2 |
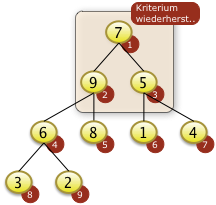 |
Bei i=1 muss f[1] mit f[2]=9 getauscht werden.
|
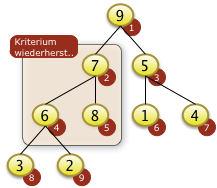 |
Nach dem Neubesetzen der Position f[2]=7 zeigt sich aber, dass die Heapbedingung für den entsprechenden Teilbaum von f[2] nicht gilt da f[2|<f[2*i+1] ist. f[2] muss also rekursiv weiter versickert werden. |
 |
Nach dem Tauschen von f[2]=7 mit f[5]=8 ist das rekursive Versickern beendet. f[5] hat keine Unterknoten da 5 > N/2 ist. Der Baum genügt jetzt der Heapbedingung |
- 10585 views
3ter Schritt...
Beim dritten Schritt müsste es doch f[4]=6 sein,welches größer ist als f[8] und f[9]...?
Bei i=2 muss f[4] mit f[2] getauscht werden. Das rekursives Versickern bei f[4]=9(6) ist nicht notwendig. f[4]=9(nicht 6?) ist größer als f[8]=3 und f[9]=2
- Log in to post comments
Positionen
1. Spalte:
Die Schlüssel f[9] bis f[5] können nicht versickert werden, da sie keine Blattknoten zum Versickern haben.
- Log in to post comments
Herstellen der Heapbedingung durch Versickern (Top-Down Methode)
Herstellen der Heapbedingung durch Versickern (Top-Down Methode)Herstellen der Heapbedingung
Top-Down-Verfahren
Dieses Verfahren dient der Herstellen der Heapbedingung, wenn schon für die Unterheaps für die Heapbedingung gilt.
Man wendet es an, nachdem man den größten Schlüssel entnommen hat und ihn durch den Wert mit dem größten Index im unsortierten Baum ersetzt hat.
Das Versickern dieses neuen Schlüssels an der Wurzel des Baums erfolgt mit den folgenden Schritten:
- Beginne mit der Position i=1 im Baum
- Der Schlüssel f[i] hat keine Unterknoten da 2*i>N ist,
- Der Schlüssel kann nicht mehr versickert werden. Das Verfahren ist beendet.
- Der Schlüssel f[i] hat noch genau einen Unterknoten f[i*2]
- Der Schlüssel f[i] wird mit dem Schlüssel f[i*2] getauscht falls f[i]<f[i*2]. Das Verfahren ist nach diesem Schritt beendet.
- Der Schlüssel f[i] hat noch Unterknoten f[2*i] und f[2*i+1]
- Der Schlüssel f[i] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Das Verfahren ist beendet die Heapbedingung ist gegeben
- Der Schlüssel f[i*2] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Tausche die Schlüssel f[i] mit f[2*i]
- Versickere den Schlüssel f[i*2] nach dem Top-Down Verfahren
- Der Schlüssel f[i*2+1] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
- Tausche die Schlüssel f[i] mit f[2*i+1]
- Versickere den Schlüssel f[i*2+1] nach dem Top-Down Verfahren
- Der Schlüssel f[i] ist der größte der drei Schlüssel f[i], f[i*2],f[i*2+1]
Diese rekursive Verfahren wird hier an einem Beispiel gezeigt:
| Grafische Visualisierung | Beschreibung |
|---|---|
 |
Durch das Entfernen des größten Schlüssels f[1] entstehen zwei Unterbäume für die die Heapbedingung nach wie vor gilt. |
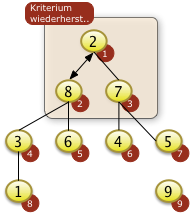 |
Durch das Einsetzen eines Schlüssel von der Position N ist nicht mehr garantiert, dass die Heapbedingung für den gesamten Restbaum f[1] bis f[N-1]=f[8] gegeben ist. Der Schlüssel f[1]=2 ist eventuell größer als die Schlüssel f[2*1] und f[2*1+1]. In diesem Fall ist die Heapbedingung für f[1] bis f[8] schon gegeben. Es muss nichts mehr getan werden. Im vorliegenden Fall ist f[1]=2 aber nicht der größte Schlüssel. Er muss rekursiv versickert werden. Dies geschieht durch das Vertauschen mit f[2] = 8. f[3] = 7 ist nicht der richtige Kandidat. 7 ist nicht der größte der drei Schlüssel. |
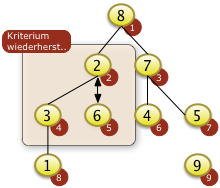 |
Nach dem Vertauschen von f[1] mit f[2] gilt die Heapbedingung zwar für den obersten Knoten. Sie gilt jedoch nicht für den Teilbaum unter f[2]= 2. Der Schlüssel 2 muss weiter versickert werden. In diesem Fall ist f[5]=6 der größte Schlüssel mit dem f[2]= 2 vertauscht weden muss. |
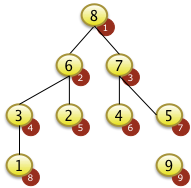 |
Nach dem Vertauschen von f[2] mit f[5] gilt die Heapbedingung wieder für den gesamten Baum. |
- 6963 views
Der Satz "Man wendet es an,
Der Satz "Man wendet es an, nachdem man den größten Schlüssel entnommen hat und ihn durch einen zufälligen Wert ersetzt hat." ist missverständlich formuliert.
Der Wert wird nicht zufällig ausgewählt, sondern ist der letzte im Baum verbliebene Knoten.
- Log in to post comments
Im Schritt 2 ist auch wieder
Im Schritt 2 ist auch wieder das "zufällig" irreführend, da der Wert ja nicht aus der Luft gezaubert wird, sondern von/auf Position N vorgegeben ist. (Ob die Werte des Heaps zufällig erstellt wurden, ist hier ja nicht von Bedeutung.)
( + typo )
"Durch das Einsetzen eines zufälligen Schlüssels von der Position N ist nicht mehr garantiert, dass die Heapbedingung für den gesamten Restbaum f[1] bis f[N-1]=f[8] gegeben ist."
- Log in to post comments
Dieses Verfahren dient der Herstellen der Heapbedingung wenn sch
Sollte geändert werden in: "Dieses Verfahren dient dem Herstellen der Heapbedingung, wenn schon für Unterheaps die Heapbedingung gilt."
- Log in to post comments
Danke, für das Feedback
Das Kommando habe ich eingefügt. Der Artikel "die" habe ich gelassen.
- Log in to post comments
Heapsort: Implementierung in Java
Heapsort: Implementierung in Javapackage s2.sort;
/**
*
* @author sschneid
* @version 2.0
*/
public class HeapSort extends Sortierer{
/**
* Konstruktor: Akzeptiere ein Feld von int. Reiche
* das Feld an die Oberklasse weiter.
* Der Algorithmus ist nicht parallel (false Argument)
* @param s
*/
public HeapSort(int[] s) {super(s,false);}
/**
* sortiert ein Eingabefeld s
* @param s ein unsortiertes Feld
* @return ein sortiertes Feld
*/
public void sortieren(int startIndex, int endeIndex){
// Erzeugen der Heapbedingung, Bottom up...
for (int i=(endeIndex-1)/2; i>=0; i--) versickere (i,endeIndex);
//System.out.println("Heapbedingung hergestellt");
for (int i=endeIndex; i>0; i--) {
// Tausche das jeweils letzte Element mit dem Groeßten an der
// Wurzel. Versickere die neue Wurzel und verkürze
// das zu sortierende Intervall von hinten nach vorne
tausche(0,i); // Groesstes Element von der Wurzel an das Ende
// des Intervals getauscht
versickere(0,i-1); // versickere die neue Wurzel um Heapbedingung
// herzustellen
}
}
/**
* Berechne Index des linken Sohns für gegebenen Index
* liefere -1 zurück falls keine linker Sohn existiert
* @param index für den Sohn berechnet wird
* @param endeIndex letzter belegter Indexplatz
* @return
*/
private int linkerSohn(int index, int endeIndex) {
int ls = index*2+1;
if (ls > endeIndex)
return -1;
else return ls;
}
/**
* Berechne Index des linken Sohns für gegebenen Index
* liefere -1 zurück falls keine linker Sohn existiert
* @param index für den Sohn berechnet wird
* @param endeIndex letzter belegter Indexplatz
* @return
*/
private int rechterSohn(int index, int endeIndex) {
int rs = (index+1)*2;
if (rs > endeIndex)
return -1;
else return rs;
}
/**
* Versickere ein Element auf der Position "vers"
* @param vers Index des zu versickernden Elements
* @param endeIndex hoechste Indexposition die zum Verisckern zur Verfügung
* steht. Sie wird bei der Berechnung des rechts Sohns
* benötigt
*/
private void versickere (int vers, int endeIndex) {
int ls = linkerSohn(vers,endeIndex);
int rs = rechterSohn(vers,endeIndex);
int groessererSohn;
while (ls != -1) { // Es gibt einen linken Sohn
// Versickere bis Heapbedingung erfüllt ist oder keine
// Söhne mehr vorhanden sind
groessererSohn =ls; // linker Sohn als groesseren Sohn nominieren
if ((rs != -1) && (istKleiner(ls,rs))) groessererSohn = rs;
// der rechte Sohn existiert und war groesser...
if (istKleiner(vers,groessererSohn)) {
tausche(vers,groessererSohn); // beide Felder wurden getauscht
vers = groessererSohn;
ls = linkerSohn(vers,endeIndex);
rs = rechterSohn(vers,endeIndex);
}
else ls=-1; // Abbruchbedingung für while Schleife
}
}
/**
* Liefert den Namen des Heap Sorts
* @return
*/
public String algorithmus() {return "Heap Sort";}
}
- 5973 views
Zusammenfassung
ZusammenfassungAufwände der vorgestellten SortieralgorithmenO(N2)
| Cmin | Caver | Cmax | Mmin | Maver | Mmax | |
|---|---|---|---|---|---|---|
| Selectionsort | O(N2) | O(N2) | O(N2) | O(N) | O(N) | O(N) |
| Insertionsort | O(N) | O(N2) | O(N2) | O(N) | O(N2) | O(N2) |
| Bubblesort | O(N) | O(N2) | O(N2) | O(0) | O(N2) | O(N2) |
| Quicksort | O(NlogN) | O(NlogN) | O(N2) | O(0) | O(NlogN) | O(NlogN) |
| Heapsort* | O(NlogN) | O(NlogN) | O(NlogN) | O(NlogN) | O(NlogN) | O(NlogN) |
* Der Heapsort ist ein nicht stabiles Sortierverfahren!
Bei der Betrachtung der Gesamtlaufzeit muss auch der Speicherplatzverbrauch berücksichtigt werden:
| Min | Average | Max | Speicher | |
|---|---|---|---|---|
| Selectionsort | O(N2) | O(N2) | O(N2) | O(1) |
| Insertionsort | O(N) | O(N2) | O(N2) | O(1) |
| Bubblesort | O(N) | O(N2) | O(N2) | O(1) |
| Quicksort | O(NlogN) | O(NlogN) | O(N2) | O(logN) |
| Heapsort | O(NlogN) | O(NlogN) | O(NlogN) | O(1) |
Der Quicksort benötigt Speicherplatz der dem Logarithmus der zu sortierenden Anzahl der Werte abhängt. Die rekursiven Aufrufe benötigen zusätzlichen Platz zum Verwalten der Intervallgrenzen.
- 4450 views
Übungen (Sortieren)
Übungen (Sortieren)Teamübung: Analyse und Implementierung eines Sortieralgorithmus
Wählen Sie einen Algorithmus
- recherchieren Sie seine Funktion
- implementieren Sie den Algorithmus
1. Konfiguration der Laufzeitumgebung
Benutzen Sie die Beispielprogramme zum Sortieren:

- Kopieren Sie sich die Klassen Sortierer, MainSort auf ihr System
- Kopieren Sie sich die Klasse SelectionSort auf Ihr System
- "Aktivieren" Sie sich den gewünschten Sortieralgorithmus in der Klasse MainSort, Methode algorithmusAuswahl(). Alle Sortieralgorithmen sind als Kommentarzeilen vorhanden. Das Entfernen genau eines Kommentar's aktiviert den gewünschten Algorithmus. Beginnen Sie zum Testen mit der Referenzimplementierung der Klasse SelectionSort.
Testen Sie die Gesamtanwendung durch das Aufrufen des Hauptprogramms MainSort.
In diesem Fall beginnt das Programm ein kleines Feld zu sortieren und gibt die Anzahl der Vergleiche, Vertauschungen, Größe des Feldes und die benötigte Zeit in Millisekunden aus. Dies ist die Phase 1. Wurde das kleine Feld erfolgreich sortiert beginnt Phase 2. Hier wird die Feldgröße jeweils verdoppelt. Das Programm bricht ab nachdem zum ersten Mal eine Zeitgrenze (3 Sekunden) beim Sortieren überschritten wurde. Hiermit lässt sich die Effizienz des Algorithmus testen und die Komplexitätsabschätzungen kontrollieren.
2. Implementieren Sie den neuen Sortieralgorithmus
Orientieren Sie sich am Beispiel der Klasse SelectionSort
- Erzeugen Sie eine neue Klasse, die aus der Klasse Sortierer abgeleitet wird
- Implementieren sie einen einfachen Konstruktor der das übergebene Feld an die Oberklasse Sortierer weiterreicht:
-
public XYSort(Sortierbar[] s) {super(s);}
-
- Implementieren Sie eine Methode mit dem Namen algorithmus() die den Namen des Algorithmus ausgibt
-
public String algorithmus() {return "XYsort";}
-
- Implementieren Sie den eigentlichen Sortieralgorithmus in der Methode public void sortieren(anfang, ende)
- Diese Methode soll als Ergebnis alle Elemente von der Position anfang im Feld bis zum Feldelement ende aufsteigend sortiert haben.
2.1 Infrastruktur für die Methode sortieren(anfang, ende)
Die Oberklasse Sortierer stellt alles zur Verfügung was man zum Sortieren benötigt
- tausche(x,y) erlaubt das Tauschen zweier Feldelemente auf der Position x mit dem Element auf der Position y
- boolean istKleiner(x,y) gibt den Wert true (wahr) zurück wenn der Inhalt der Feldposition x kleiner als der Inhalt der Feldposition y ist
Diese beiden Hilfsmethoden sind die einzigen Methoden die zum Implementieren benötigt werden. Der Typ des zu sortierenden Feldes bleibt hinter dem Interface Sortierbar verborgen. Im vorliegenden Fall sind es ganze Zahlen.
Um die Entwicklung zu Vereinfachen bietet die abstrakte Klasse Sortieren eine Reihe von Hilfsmethoden:
- druckenKonsole(): druckt das gesamt Feld mit seiner Belegung auf der Konsole aus
- generiereZufallsbelegung(): Belegt ein existierendes Feld mit neuen Testdaten
- long anzahlVertauschungen(): Gibt die Zahl der Vertauschungen an. Sie werden durch Aufrufe von tausche() gezählt
- long anzahl Vergleiche(): Gibt die Zahl der Vergleiche aus. Sie werden durch Aufrufe von istKleiner() gezählt
- boolean validierung(): Erlaubt die Prüfung eines sortierten Felds. Der Wert ist wahr wenn das Feld korrekt sortiert ist.
3. Anpassen des Hauptprogramms MainSort
Das Hauptprogramm MainSort erzeugt an einer Stelle eine Instanz der Klasse SelectionSort. Ändern Sie diese Stelle im Programm derart, dass eine Instanz Ihrer neuen Sortierklasse aufgerufen wird.
4. Vorbereitende Tests für die Präsentation
Ändern Sie die zu sortierenden Testdaten im Programm MainSort derart ab, dass Sie
- den ungünstigsten Fall für den Sortieralgorithmus wählen (Vertauschungen, Prüfungen)
- den günstigsten Fall wählen (Vertauschungen, Prüfungen)
Tragen Sie die abgelesen Werte in eine Tabellenkalkulation ein und prüfen Sie ob die Aufwände mit den Vorhersagen des Lehrbuchs übereinstimmen (Grafiken!)
Bereiten Sie eine 15-20 minütige Vorstellung/Präsentation des Algorithmus vor:
- Erklären des Algorithmus (mit Beispiel)
- Tafel, Folie, Overheadprojektor genügen
- Vorführen einer Implementierung
- Komplexitätsüberlegungen und Bewertung
- Was ist der durchschnittliche Aufwand?
- Was ist der minimale Aufwand (Beispiel)?
- Wählen Sie die Anzahl der Vertauschungen oder der Vergleiche
- Was ist der Aufwand im ungünstigsten Fall (Beispiel)?
- Wählen Sie die Anzahl der Vertauschungen oder der Vergleiche
- Wichtige Punkte die abhängig vom Algorithmus beachtet werden sollen
- Sortieren durch Auswahl
- Präsentation
- Erklären Sie die "Sortiergrenze"
- Präsentation
- Bubblesort
- Präsentation
- Welche Elemente werden immer vertauscht?
- Warum ist diese Strategie intuitiv aber nicht effizient?
- Präsentation
- Quicksort
- Nutzen Sie Bleistifte oder Streichhölzer zum Visualieren des Verfahrens.
- Legen Sie das Pivotelement in Ihrer Implementierung der Einfachheit halber an eine feste Intervallgrenze!
- Algorithmus:
- Erklären Sie das grundlegende Konzept des Quicksorts (3 Sätze reichen hier!)
- Erklären Sie die Rekursion (Teile und Herrsche) und das Ende der Rekursion (Abbruch)
- Implementierung
- Erklären Sie den Begriff des "Pivotelement"
- Die Implementierung ist durchaus kompliziert. Skizieren Sie sie nur.
- Heapsort
- Diskutieren Sie den Dualismus der beiden Zugriffstrukturen
- Sie arbeiten auf einem Feld (Array)
- Sie betrachten auf der abstrakten Ebene einen Baum
- Wie ist der Zusammenhang zwischen Blattknoten und Feldpositionen?
- Implementierung
- Schreiben Sie Methoden zur Bestimmung der linken und rechten Blattknoten
- Schreiben Sie eine Methode zum Versickern
- Präsentation
- Erläutern Sie den Dualismus
- Erläutern Sie die Bestimmung der Blattknoten
- Erläutern Sie die "Heapbedingung"
- Wie wird sie hergestellt
- Erläutern Sie das Konzept des "Versickerns"
- Diskutieren Sie den Dualismus der beiden Zugriffstrukturen
- Referenzen aus dem Internet
- Zeigen die Referenzen, die Sie am besten mögen: Lustig, lehrreich, witzig
- Zusammenfassung:
- Wie mögen Sie den Algorithmus?
- Wie aufwendig war die Implementierung?
- Sortieren durch Auswahl
- 4983 views
Backtracking
BacktrackingEs gibt drei Arten von Backtracking:
- Entscheidungsproblem: Hier wird eine Lösung gesucht
- Optimierungsproblem: Hier wird die beste Lösung gesucht.
- Aufzählungsproblem: Hier werden alle Lösungen gesucht.
 |
Welche Beispiele aus dem echten Leben gibt es für diese drei Kategorien? |
| Definition (nach Wikipedia) |
|---|
| Backtracking geht nach dem Versuch-und-Irrtum-Prinzip (trial and error) vor, das heißt, es wird versucht, eine erreichte Teillösung zu einer Gesamtlösung auszubauen. Wenn absehbar ist, dass eine Teillösung nicht zu einer endgültigen Lösung führen kann, wird der letzte Schritt beziehungsweise werden die letzten Schritte zurückgenommen, und es werden stattdessen alternative Wege probiert. Auf diese Weise ist sichergestellt, dass alle in Frage kommenden Lösungswege ausprobiert werden können (Prinzip des Ariadnefadens). Mit Backtracking-Algorithmen wird eine vorhandene Lösung entweder gefunden (unter Umständen nach sehr langer Laufzeit), oder es kann definitiv ausgesagt werden, dass keine Lösung existiert. Backtracking wird meistens am einfachsten rekursiv implementiert und ist ein prototypischer Anwendungsfall von Rekursion. |
Zeitkomplexität (nach Wikipedia)
Bei der Tiefensuche werden bei maximal z möglichen Verzweigungen von jeder Teillösung aus und einem Lösungsbaum mit maximaler Tiefe von N im schlechtesten Fall 1+z+z2+z3+⋯+zN Knoten erweitert.
Die Tiefensuche und somit auch Backtracking haben im schlechtesten Fall mit O(zN) und einem Verzweigungsgrad z>1 eine exponentielle Laufzeit. Je größer die Suchtiefe n, desto länger dauert die Suche nach einer Lösung. Daher ist das Backtracking primär für Probleme mit einem kleinen Lösungsbaum geeignet.
Resourcen
- 1266 views
Hashverfahren
HashverfahrenHashverfahren helfen Datensätze zu speichern und effizient Operationen wie Suchen, Einfügen und Entfernen zu unterstützen.
Die Datensätze werden mit Hilfe eines eindeutigen Schlüssels gesucht bzw. sortiert. Die Idee der Hashverfahren basiert auf dem Fakt, dass in einer zu verwaltenden Menge, die Anzahl der Schlüssel normalerweise deutlich kleiner als die Wertemenge K der Schlüssel ist. Zu jedem Zeitpunkt ist also nur eine (kleine) Teilmenge K aller möglichlichen Schlüssel gespeichert. Dies geschehe in einem linearen Feld mit Indizes 0, ... , m-1. Diese nennt man Hashtabelle. m ist die Größe der Hashtabelle.
Eine Hashfunktion h ordnet jedem Schlüssel k einen Index h(k) zu. Für h(k) gilt: 0 <= h(k) <) m-1. Im Allgemeinen ist m-1 sehr viel kleiner als der Wertebereich der Schlüssel. Die Hashfunktion kann im Allgemeinen nicht injektiv und weist unterschiedlichen Werten die gleiche Hashadresse zu.
Zwei Schlüssel h(k) und h(k') mit h(k)=h(k') nennt man Synonyme.
Treten in der Menge K keine Synonyme auf, können Sie direkt in der Hashtabelle an der entsprechenden Stelle gespeichert werden.
Im folgenden Beispiel wird als h(k) h(k)= k mod 10 verwendet. Es wird hier also von jeder Jahl der Rest einer Division durch 10 verwendet (Man könnte auch sagen die letzte Stelle...)
|
Hier treten keine Synonyme auf. Die Abildung ist eineindeutig.
|
Hier tritt eine Kollision mit Synonymen auf die Werte 0 und 50 werden auf den Tabellenwert 0 abgebildet.
|
Treten Synonyme auf, ist dies schlecht für ein Hashverfahren. Der konstante Aufwand der Berechnung der Hashfunktion und der Zugriff im Feld führen zu einer Kollision die aufgelöst werden muss.
Ein Hashverfahren soll
- möglichst wenige Kollisionen aufweisen
- Adresskollisionen sollen möglichst effizient aufgelöst werden
| Aufwand | minimaler Aufw. | maximaler Aufw. | Kommentar |
|---|---|---|---|
| Suchen/Einfügen | O(1) | O(n) | Das Auftreten von Synonymen macht den Unterschied! |
Die Berechnung der Hashfunktion sollte einen konstanten Aufwand haben.
Der Zugriffsaufwand steigt aber beim Auftreten von Kollisionen. Die Probleme bei den Hashverfahren liegen in der Auflösung von Kollisionen und beim Wachsen über die Größe eines Feldes. Für eine tiefere Diskussion fehlt in dieser Vorlesung leider die Zeit. Anbei zwei gängige Strategien:
Hashverfahren mit Verkettung der Überläufer
|
Ein Lösungsansatz besteht in der Verkettung von Überläufern deren Hashfunktion Synonyme produziert. Dies geschieht rechts bei den Werten 0 und 50. Der Zugriffsaufwand ohne Synonyme für EInfügen und Lesen ist hier O(1). Liegen Synonyme vor ist der Aufwand O(n). Die Verkettung funktioniert wenn in die Hashtabelle nur Zeiger eingetragen werden. |
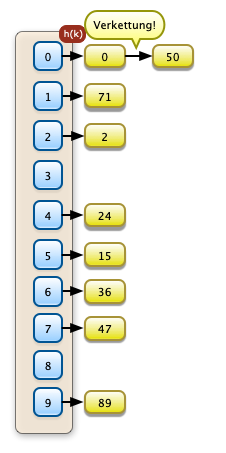 |
Offene Hashverfahren
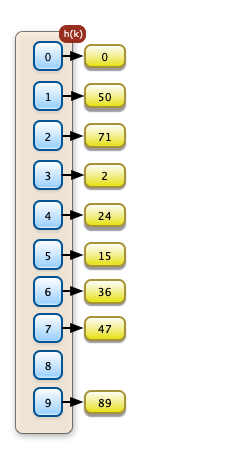 |
Sollen die Objekte direkt im Feld gespeichert werden, muß man sich im Feld einen neuen Platz suchen. Im Schaubild links, wurde zuerst die "0" auf ihrem Platz korrekt eingetragen. Als nächstes wurde die "50" eingetragen. Für sie war der Platz 0 schon belegt. Sie wurde auf dem Platz 1 eingetragen. Dann wurde die "71" eingetragen. Ihre Position 1 war schon belegt. Sie wurde auf der Position 2 eingetragen. Der Eintrag der "2" auf der Position 2 war auch nicht mehr möglich. Sie musste auf der Position 3 gespeichert werden. Ein Überläufer kann hier einen Ketteneffekt produzieren. Das Einfügen und das Finden können aufwendiger werden. Diese Operationen können im schlimmsten Fall den Aufwand O(n) haben. |
Hashverfahren robust gegen Sonderfälle zu machen ist recht aufwendig und sprengt den Rahmen dieser Vorlesung.
- 521 views
Teile und Herrsche Paradigma
Teile und Herrsche ParadigmaGrundprinzip[ (nach Wikipedia)
Bei einem Teile-und-herrsche-Ansatz wird das eigentliche – in seiner Gesamtheit – als zu schwierig erscheinende Problem so lange rekursiv in kleinere und einfachere Teilprobleme zerlegt, bis diese gelöst („beherrschbar“) sind. Anschließend wird aus diesen Teillösungen eine Lösung für das Gesamtproblem (re-)konstruiert.
Resourcen
- 1173 views
Lernziele
Lernziele|
|
Am Ende dieses Blocks können Sie:
|
Referenzen
T.Ottmann / P.Widmayer: Algorithmen und Datenstrukturen: Kapitel Sortieren
Lernzielkontrolle
Sie sind in der Lage die folgenden Fragen zu beantworten: Fragen zu Algorithmen
Feedback

- 3374 views